博客基于GAMES101-现代计算机图形学入门-闫令琪，但不是其完整笔记，基于复习要求有一定的删减。
考试以图形学入门基本概念和核心研究内容为主，少量公式。即以论述概念为主，涉及少量算法。
p1:29:12是对应的games101视频节点（第一个视频的29分12秒附近）。

文章目录

📚图形学的技术挑战
📚图形学与计算机视觉
📚线性代数复习
- 🐇点乘在图形学的应用
- 🐇叉乘在图形学的应用
📚变换
- 🐇矩阵变换(线性变换)
- 🐇齐次坐标⭐️
- 🐇视图变换
- 🐇投影变换
- - 🥕正交投影
  - 🥕透视投影
📚光栅化⭐️
- 🐇光栅化的概念
- 🐇采样——Inside函数⭐️
- 🐇时域和频域
- 🐇傅里叶频域图
- 🐇卷积
- 🐇超采样抗锯齿（MSAA）
- 🐇超分辨率
- 🐇画家算法
- 🐇深度缓冲（Z-Buffer）
📚着色
- 🐇Blinn-Phong反射模型
- 🐇实时渲染管线⭐️
- 🐇纹理映射
📚几何
- 🐇几何表示方法的分类
- 🐇隐式几何
- - 🥕CSG
  - 🥕距离函数
- 🐇显式几何
- - 🥕多边形网络⭐️
  - 🥕贝塞尔曲线⭐️
  - 🥕网格操作⭐️

📚图形学的技术挑战

考察有哪些技术，诸如此类，考察概念，p1:29:12

光栅化（resterization）：把三维空间的几何形体显示在屏幕上；将投影基元分解成碎片（像素）；是游戏等实时计算机图形学的主要应用。实时：能达到每秒钟三十帧（30fps）被看做是实时的，反之是离线的。

在这里插入图片描述

曲线和网格（Curves and Meshes）：如何在计算机图形学中表示几何，各种细分方法。

在这里插入图片描述

光线追踪（Ray Tracing）：通过每个像素点从相机发送光线——计算交点和阴影+继续反射光线，直到击中光源；离线应用。

效果好但是速度慢，目前游戏使用的是实时光线追踪。

在这里插入图片描述

仿真和模拟（Animation/Simulation）：关键帧动画、质量弹簧系统

在这里插入图片描述

OpenGL、DirectX是图形学API，并不是图形学

📚图形学与计算机视觉

图形学不是计算机视觉。
计算机视觉是去猜测、预测、分析处理。
计算机视觉是理解这个世界，计算机图形学是创造这个世界。

在这里插入图片描述

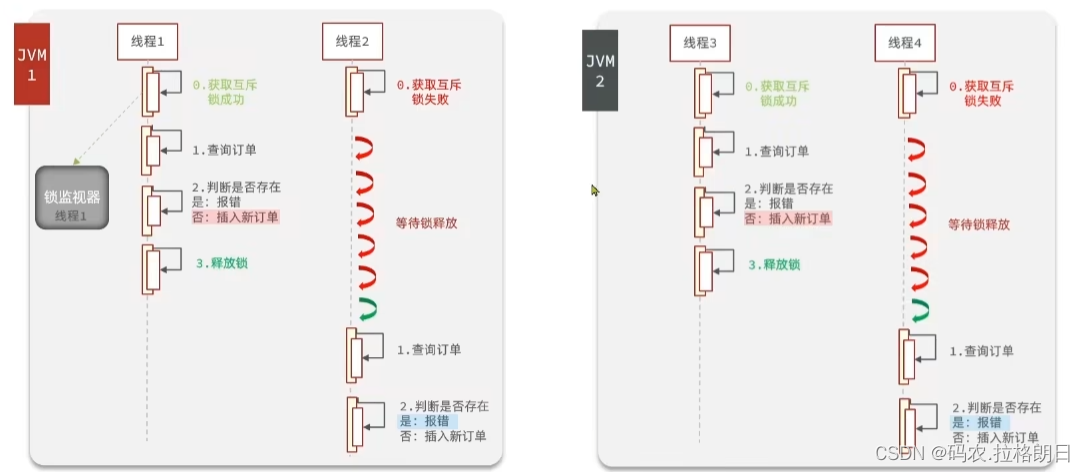
上图解释说明p1:37:08👀

📚线性代数复习

🐇点乘在图形学的应用

p2:16:48，可能会考察公式

⭕️向量点乘最后得到一个数。点乘主要应用于求夹角，特别是单位向量；

在这里插入图片描述

⭕️寻找一个矢量在另一个矢量上的投影；基于投影，进一步可以完成向量分解。

在这里插入图片描述

⭕️观察两个向量的接近（结果接近1，离得很近；接近-1，离得很远），判断前后，前（同向）、后（反向）、垂直（Dot=0)。

在这里插入图片描述

🐇叉乘在图形学的应用

p2:30:21

⭕️向量叉乘得到的是向量。

⭕️向量积与两个初始向量正交，方向由右手定则确定，用于构造坐标系。

在这里插入图片描述

⭕️判定左右（内外）：若A×B为正，则点B在点A的左侧（结合右手系，从A转到B理解），反之在右侧。

⭕️判断一个点是否在三角形内部：若AB×AP，BC×BP，CA×CP同向（都在左边或都在右边），则说明点P在△ABC内部。

在这里插入图片描述

⭕️定义坐标系：单位向量+互相垂直（点乘为0且叉乘结果为另一轴），定义坐标系后就可以把任意向量投影到坐标系。

在这里插入图片描述

📚变换

⭕️怎么用一个矩阵去表达变换，在矩阵无法表达的基础上（平移变换），怎么就引入了齐次坐标对所有的变换进行统一的表达。

🐇矩阵变换(线性变换)

p3:7:03

在这里插入图片描述

⭕️缩放

这里用于缩放的矩阵就叫缩放矩阵，以下同理

在这里插入图片描述

⭕️X轴翻转

在这里插入图片描述

⭕️切变

在y=0处水平位移为0
在y=1处水平位移为a
垂直位移总是0

在这里插入图片描述

⭕️旋转

约定：默认是绕着原点逆时针转

在这里插入图片描述

通过（1,0）（0,1）比对前后差异进行推导。

🐇齐次坐标⭐️

定义是什么？哪些地方表示旋转，哪些地方表示平移？p3:32:23

⭕️平移

在这里插入图片描述

❓平移不是线性变换，为了解决平移产生必须要用加法的问题，加入齐次坐标。

齐次坐标通过将点的坐标表示为多维向量，并在末尾添加一个额外的分量，这个额外的分量通常被称为齐次坐标。引入齐次坐标的目的就是使得所有的变换都可以写成一个矩阵乘以一个向量的形式。

❓为什么要将点和向量区分开

在这里插入图片描述

因为向量具有平移不变性。

⭕️齐次坐标转化仿射变换

仿射变换=线性变换+平移
同时需要平移和线性变换的时候，需要先线性变换再平移（矩阵不满足交换律）

在这里插入图片描述

先平移后旋转⚠️

先旋转后平移✅

⭕️齐次坐标表示缩放、旋转和平移

在这里插入图片描述

🐇视图变换

考察基本过程（每一步都干什么），p4:22:10

⭕️什么是视图变换：简言之，就是摆好摄像机。

⭕️思考如何拍一张照片?

找一个好的地方并安排好拍照的人（模型变换）
找一个好的角度并放好相机（视图变换）
茄子!（投影变换）

⭕️定义相机

相机在哪？
相机朝哪个方向？
相机的向上方向（控制歪斜）？

在这里插入图片描述

如果相机和所有的物体一起移动，“照片”将是相同的，所以干脆就让相机都移动到原点上，默认的向上方向为+Y，永远朝着-Z方向看。（物体和相机一块动，这么移动好处多多，方便又美妙）

在这里插入图片描述

⭕️把任意点相机移到默认点

首先把中心移到原点——先平移（这里相当于上述过程逆过程，所以是先平移）
把观察方向旋转到-Z方向
把向上方向旋转到Y方向
自然而然得出X方向

在这里插入图片描述

计算过程

🐇投影变换

表述两种方式的大概过程，不要求记住公式，p4:38:56

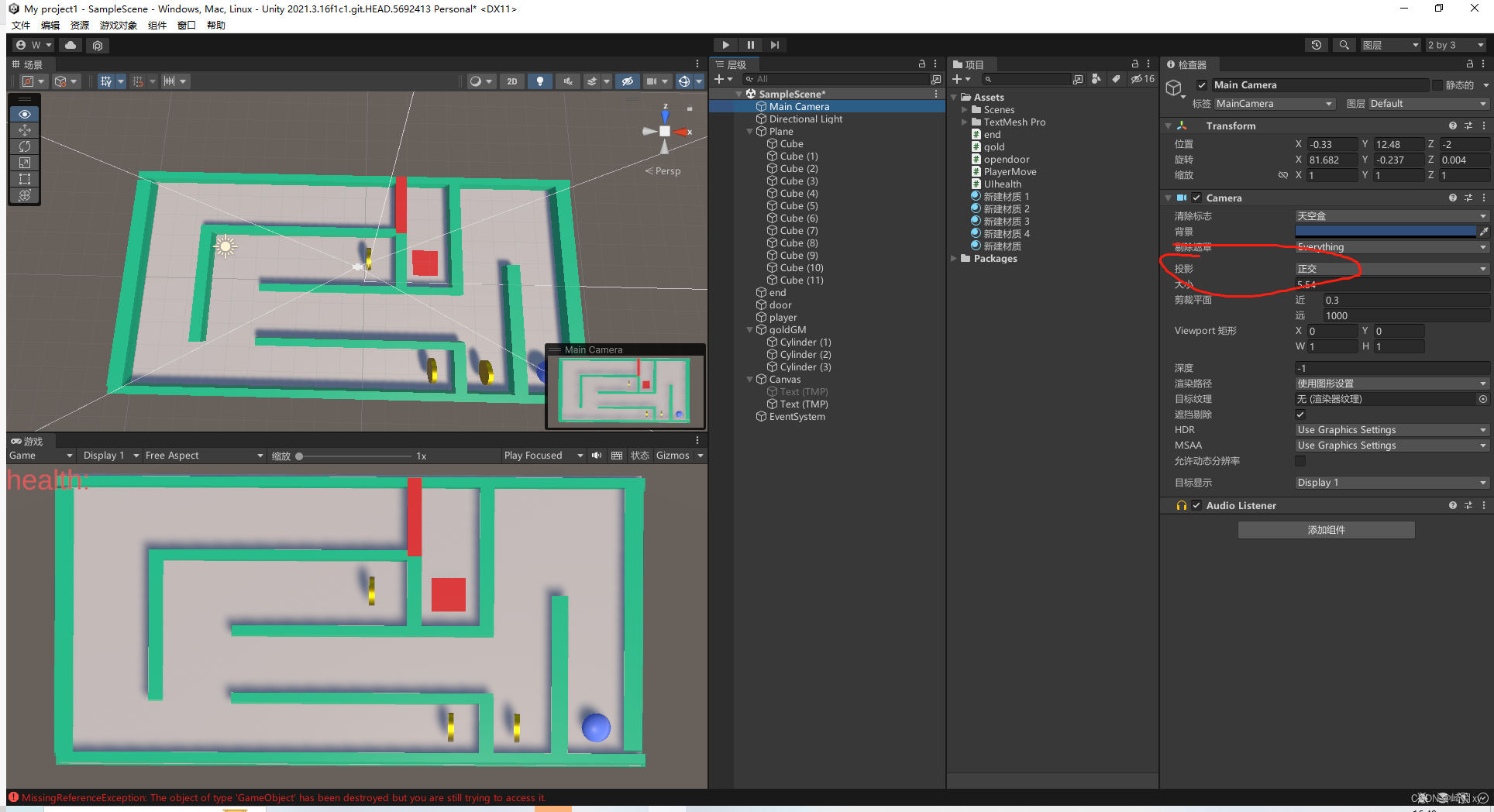
透视投影（Perspective projection)：近大远小，更类似于现实中的形态。
正交投影（Orthographic projection)：更像工程制图（可以理解为把相机放到无限远），没有近大远小的现象。

在这里插入图片描述

🥕正交投影

⭕️一种简单的理解方式

把z轴去掉
相机位于原点，看向-Z轴，向上为Y轴
将生成矩阵平移并缩放为 $1,1]^2$

在这里插入图片描述

⭕️标准方式

p4:48:55

将任意的立方体变成标准立方体，先做平移，再做缩放

在这里插入图片描述

🥕透视投影

p4:53:17

⭕️如何做透视投影

首先将截椎体“压扁”成长方体。 $M_{persp->ortho}$
然后作正交投影。 $M_{ortho}$

规定：

近平面保持不动；
远平面的Z轴不动，只有 x , y 的缩放；
位于 x = 0 , y = 0 的点保持不动。

在这里插入图片描述

⭕️“压扁”操作：利用相似三角形求出y轴的位置，同理可以得到 $x^{'} = (n / z) x$

在这里插入图片描述

⭕️Z轴如何处理

🔔完成X、Y的处理后，同时乘Z得到以下式子：

在这里插入图片描述

🔔根据已知的内容，可以先得到如下式子：

在这里插入图片描述

🔔由近平面的z就是n：

在这里插入图片描述

🔔由远平面的x=0，y=0的点，也即（0,0,f）可得：

在这里插入图片描述

🔔联立可得：Z轴一行的矩阵为（0,0,n+f,-nf)

在这里插入图片描述

小结：

📚光栅化⭐️

🐇光栅化的概念

p5:6:33

⭕️如何定义视椎体宽高比和垂直可视角度？

fov：垂直可视高度
t：在y轴的高度
n：近平面上的z轴上的点
r：中心点到右边的距离

在这里插入图片描述

⭕️屏幕

对于图形学来说，屏幕抽象为二维数组
数组中的每个元素是一个像素
屏幕是一个典型的光栅成像设备

光栅化：在屏幕上绘画

光栅化指的是将矢量图形或几何图形转换为由像素组成的栅格图像的过程.
在光栅化图形学中，矢量图形是通过数学表示的集合对象（如三角面片），而栅格图像是由像素（图像单元）组成的二维数组。

像素：
- 在屏幕上最小单位的小方块
- 由红绿蓝三原色混合而成

⭕️屏幕空间：

像素都是以（x,y）的形式表示，其中x,y都是整数
像素的范围从（0,0）到（宽度-1,长度-1）
像素的中心在（x+0.5,y+0.5)
屏幕覆盖范围为（0,0）到（宽,高）

在这里插入图片描述

🐇采样——Inside函数⭐️

⭕️在某个点对函数求值就是采样，我们通过采样将函数离散化。

⭕️Inside函数——判断像素中心是否在三角形内

描述两种点定位问题的大概思路，p5:46:02

在这里插入图片描述

🔔遍历所有点，判断所有点是否在像素内

for(int x = 0; x < xmax ; ++x)
{
    for(int y = 0; y < ymax; ++y)
    {
        image[x][y] = inside(tri, x + 0.5, y + 0.5);
    }
}

🔔实验回顾

🍉法①：通过叉乘判断

pab=Cross(PA,PB)，pbc=Cross(PB,PC)，pca=Cross(PC,PA)
如果pab,pbc,pca指向同一个方向，那就可以判断点在三角形内部
即 Dot(pab,pbc)>0 , Dot(pab,pca)>0 , Dot(pbc,pca)>0同时成立

在这里插入图片描述

🍉法②：面积法

分别求得△PAB,△PAC,△PBC和△ABC的面积
若△ABC= △PAB + △PAC + △PBC就可以判断点在三角形内部

在这里插入图片描述

🐇时域和频域

时域：描述数学函数或物理信号对时间的关系的一种坐标系
频域：描述信号在频率方面特性时用到的一种坐标系

🐇傅里叶频域图

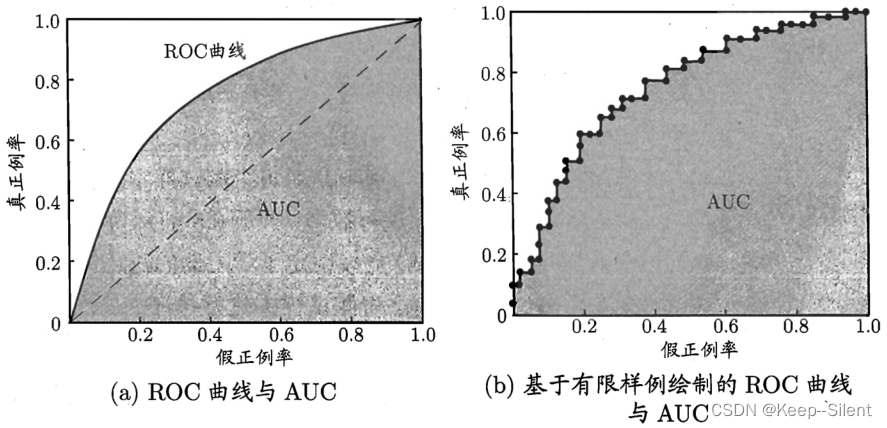
考察低通滤波和高通滤波的概念，p6:29:26

滤波：删除特定的频率被称之为滤波。

在这里插入图片描述

高通滤波：只显示高频信息，只显示边界锐化，将低频信息盖住。

在这里插入图片描述

低通滤波：只显示低频滤波，画面变模糊，将高频信息盖住。

在这里插入图片描述

🐇卷积

基本概念，可能会让大家手动计算卷积过程（二维），p6:39:50

滤波（Filtering）= 卷积（Convolution）= 平均（Averaging）

在这里插入图片描述

简化的定义：结果为相邻数的平均值

在这里插入图片描述

时域的卷积等于频域的乘积

![在这里插入图片描述](https://img-blog.csdnimg.cn/54b0522442f946a39c7f1b5401498232.png#pic_
center)

🐇超采样抗锯齿（MSAA）

锯齿——Ps：锯齿/摩尔纹/车轮效应——信号时间变化太快以至于采样跟不上变化的速度

反走样（抗锯齿）：在图像渲染过程中，当图形边缘处存在锯齿状走样时，使用抗锯齿技术可以使图像边缘更加平滑，提高图像的视觉质量。
将每个像素进行模糊卷积f(x,y)
然后再对每个像素的中心取样
在光栅化一个三角形时，像素颜色的平均值f(x,y) = 三角形的覆盖像素的面积

p6:1:04:23——MSAA（Antialiasing By Supersampling）

这是一种对反走样的近似
将每个像素的内部多增加采样点再进行模糊卷积

在这里插入图片描述

与传统的单一采样抗锯齿技术相比，MSAA可以提供更好的抗锯齿效果，但增加了很多的计算量。

🐇超分辨率

基本概念，p6:1:16:50

从低分辨率处理成高分辨率
与反走样类似，也是解决了样本不足的问题
目前可使用DLSS（深度学习的方法）进行超分辨率处理（缺失的部分猜出来

🐇画家算法

基本概念，p7:4:49

灵感来源于画优化
先画（渲染）距离远的，再画（渲染）距离近的。

在这里插入图片描述

问题：难以确定谁在前谁在后？

在这里插入图片描述

🐇深度缓冲（Z-Buffer）

基本概念，p7:10:35

深度图：储存每个像素对应的最浅的深度
结果图：储存最终的结果
Z越小（越黑）越近，越大越远

在这里插入图片描述

算法流程：

在这里插入图片描述

深度缓存迭代示例：

在这里插入图片描述

📚着色

⭕️着色：对不同的物体应用不同的材质。

🐇Blinn-Phong反射模型

高光、漫反射和环境光照分别是什么？p7:37:57

⭕️高光（Specular highlights）：它是由于光线照射到光滑表面上并以相同角度反射而产生的明亮点或区域。高光通常呈现为物体表面的亮点或反射光斑，可以提供物体的光泽感和反射特性。

⭕️漫反射（Diffuse reflection）：**当光线照射到粗糙表面上时，均匀地反射到各个方向的光线。**漫反射不会像高光那样形成明亮的反射光斑，而是在整个物体表面均匀分布的光线。漫反射对于物体的整体亮度和颜色起到重要作用，它使物体看起来不那么光滑，更加真实。

⭕️环境光照（Ambient lighting）：**来自于周围环境的间接光照。**它是由光线在环境中多次反射、散射后到达物体表面的光线。环境光照是一种均匀分布的光照，没有特定的光源方向和强度。

在这里插入图片描述

🔔漫反射——兰伯特余弦定理

p7:47:50

兰伯特余弦定律： $cos θ = l \cdot n$
n：法线方向；l：光照方向
不同角度物体的反射的光不同

在这里插入图片描述

🐇实时渲染管线⭐️

流程考察概率高，p8:32:47

⭕️简化的流程：从三维场景到最后渲染出二维图像的过程

输入空间中一系列的点
顶点处理
三角形处理
光栅化
着色
- 片段（像素）处理
- 帧缓冲区处理
输出

在这里插入图片描述

目前渲染管线都是在GPU里被编程完成了，只有顶点处理和片段处理可以编程

🐇纹理映射

p8:54:50

⭕️纹理映射

纹理映射就是定义任意点的基本属性
每个三维模型上的任意点都能对应在uv坐标上的某个点上

在这里插入图片描述

纹理可以被重复使用

在这里插入图片描述

纹理是指一张或多张图像，用于覆盖（或映射）到三维模型的表面上，以增加模型的细节和真实感。
着色是指为三维模型的表面赋予颜色和光照效果的过程。

⭕️重心坐标（定义与性质）

这个基本公式可能会考察，p9:4:20

为什么要插值❓为了获取平滑的过渡
插值的内容有哪些❓纹理坐标、颜色、法向量
如何做插值❓重心坐标

重心坐标是定义在三角形上的，在三角形ABC所形成的平面内（仅需要满足α+β+γ=1）任意一个点（x,y）都可以表示为三个顶点ABC坐标的线性组合。
若α、β、γ均为非负数，则（x,y）点一定在三角形内。

在这里插入图片描述

面积法求解：

在这里插入图片描述

三角形重心坐标：（三分面积）

在这里插入图片描述

任意一点的重心坐标公式求解：

在这里插入图片描述

插值的应用：通过获得ABC点的值来获取到三角形内任意坐标的位置、颜色、法线、深度等信息；值得注意的是，在投影下不能保证坐标不变，所以要先插值再进行投影。

⭕️应用材质

p9:20:57

将原本在各个顶点上的值，通过中心坐标插值到uv以及纹理坐标上的屏幕上的每个采样点上，纹理定义的值就是漫反射的系数 $K_d$

💛纹理太小了怎么办❓——双线性插值：通过考虑原始图像中四个相邻像素的值和权重，生成平滑的缩放图像

p9:23:45

在这里插入图片描述

双线性插值（中，取邻近四个）和双三线性插值（右，取邻近16个），以下为双线性插值处理步骤

找到（s,t），s、t都在0-1之间

在这里插入图片描述

进行线性插值：先上下两点的水平插值，再进行竖直的插值。（也可以先竖直后水平）

在这里插入图片描述

得到红点对应的值，红点综合考虑了四个相邻像素的值和权重，例如rgb值。

💛纹理太大了怎么办——Mipmap操作

p9:35:01

纹理太大，近处锯齿，远处摩尔纹——像素覆盖的纹理区域大的时候，不能简单以中心点去采样

可用超采样，就是取很多点，但是costly！

Mipmap

p9:44:01，Mipmap（从一张图生成一系列图）只能做近似的正方形的范围查询

level0是原始图像，每提高一个level，分辨率小一倍，利用相邻的四个像素的rgb作平均值
mipmap的额外存储量是原始的⅓

在这里插入图片描述

近似算正方形区域：

在这里插入图片描述

Mipmap操作：
- 在屏幕空间中取当前像素相邻的像素并查询其对应的uv坐标
- 计算出当前像素点与其他像素点距离其他像素点的最大值
- 根据最大值L通过上面公式计算得到该点所处的层数D

👀AI概念辅助理解：

在计算机图形学中，纹理映射是将二维图像（纹理）映射到三维模型表面上的过程。
当一个纹理被应用到一个远离相机的表面时，原始纹理可能会因为距离较远而产生细节丢失和失真。这是由于远处的表面像素与相机之间的距离较远，导致原始纹理中的细节无法完全呈现。
Mipmap是一组预先生成的纹理图像，其中每个图像都是原始纹理的不同大小和分辨率的版本。最底层的Mipmap级别是原始纹理的完整大小，而每个后续级别都是前一个级别的一半大小。
核心思想是，当渲染远离相机的表面时，使用较小的Mipmap级别，而当渲染靠近相机的表面时，使用较大的Mipmap级别。这样可以避免在远处使用原始纹理时产生的细节丢失和失真问题。
通过选择合适的Mipmap级别，可以根据距离和表面大小来平衡图像质量和渲染性能。

📚几何

🐇几何表示方法的分类

p10:46:05

⭕️隐式（implicit)

可以通过一个函数来表示的集合体。
例如圆可以表示为 $f (x, y, x) = 0$ 。
优点：可以很容易判断某个点是否在几何体上。
缺点：难以通过函数判断出几何体的真实形状。

⭕️显式（Explicit）

通过参数映射（通过某个带有u,v的函数分别表示出x,y,z的坐标）表示表示的集合体。
直接给出几何体。
优点：容易看出几何体的真实形状。
缺点：难以表示出某个点是否在几何体上。

🐇隐式几何

🥕CSG

p10:58:18

复杂的几何体通过简单几何体进行集合运算（交并补）得到，该操作被称之为CSG。

在这里插入图片描述

🥕距离函数

p10:1:01:01

在这里插入图片描述

下图A与B进行融合操作后得到的blend(A,B)，左边三分之一完全被挡住，中间被挡住一半，最后边完全被挡住。通过AB距离函数相加得到融合后的SDF图，可以转化为blend(A,B)这张图。
距离函数：任何一个点到达边界的最短距离。

p10:1:03:29

在这里插入图片描述

距离函数通过水平集得到 $f (x) = 0$

在这里插入图片描述

🐇显式几何

🥕多边形网络⭐️

p11:5:36

⭕️简介：将面拆解为多边形（大多是三角形和四边形），存储顶点和多边形信息。在图形学中应用最为广泛。

⭕️如何存储多边形信息：

使用OBJ格式将几何体的点、法线、纹理坐标分别表示，然后再表示面与面的连接关系。
下图定义了一个立方体，有八个顶点（v)，六个面（Vn），多个纹理坐标（vt）表示，然后使用f表示他们之间的关系（f V/Vt/Vn）

在这里插入图片描述

🥕贝塞尔曲线⭐️

算法，p11:13:02

⭕️贝塞尔曲线：只要求一定要经过起止点，起止点之间的若干个控制点用于控制曲线弯曲的方向，最终形成一条经过起止点的光滑曲线，被称为贝塞尔曲线。

在这里插入图片描述

⭕️德卡斯特利奥算法

p11:15:45

算法流程：

引入参数t（范围为0-1）
取 $b_0$ 到 $b_1$ ， $b_1$ 到 $b_2$ 上t位置的点 $b_0^{'}$ ， $b_1^{'}$
将 $b_0^{'}$ ， $b_1^{'}$ 连接
取 $b_0^{'}$ ， $b_1^{'}$ 的t位置上的点 $b_0^{"}$

在这里插入图片描述

将所有的0-1的 $b_0^{"}$ 点都遍历一份相连即可得到贝塞尔曲线
若有n个控制点则将上面步骤进行递归操作直到找到最终位移 $b_0^{n}$

在这里插入图片描述

公式

在这里插入图片描述

一般地：

可以求得一个以t为自变量的函数，由这些点形成的集合构成贝塞尔曲线
$b$ 为n个贝塞尔控制点
$B^n$ 为伯恩斯坦多项式

在这里插入图片描述

对贝塞尔曲线做仿射变换只需要对控制点、起止点做仿射变换再重新绘制一遍即可。

🥕网格操作⭐️

需掌握两种细分方法的顶点更新公式

网格细分：让网格的面数更多
网格简化：让网格的面数更少
网格正规化：让网格中的三角形趋近于正三角形

⭕️Loop细分

p12:9:32，只能对完全为三角形的几何体进行细分

将每个三角形变为4个三角形，根据权重指定新的顶点位置，新老顶点以不同的规则来改变自己的位置：

在这里插入图片描述

对于新的顶点：V' = 3/8 * (A + B) + 1/8 * (C + D)
- $V^{'}$ 为新的顶点变换后的位置
- A、B为两个面被共享边的老顶点
- C、D为非共享边的两个顶点
对于旧的顶点：V' = (1 - n*u) * original_position + u * neighbor_position_sum
- V’为旧的顶点变换后的位置
- n为顶点的度（链接的顶点数）
- 如果n=3则u=3/16，其他情况u=3/(8n)
- original_position为旧顶点原本的位置
- neighbor_position_sum为邻居点的平均位置