本文来自公众号“AI大道理”

 ——————

距离度量在CV 、NLP以及数据分析等领域都有众多的应用。

距离度量可以当做某种相似度，距离越近，越相似。

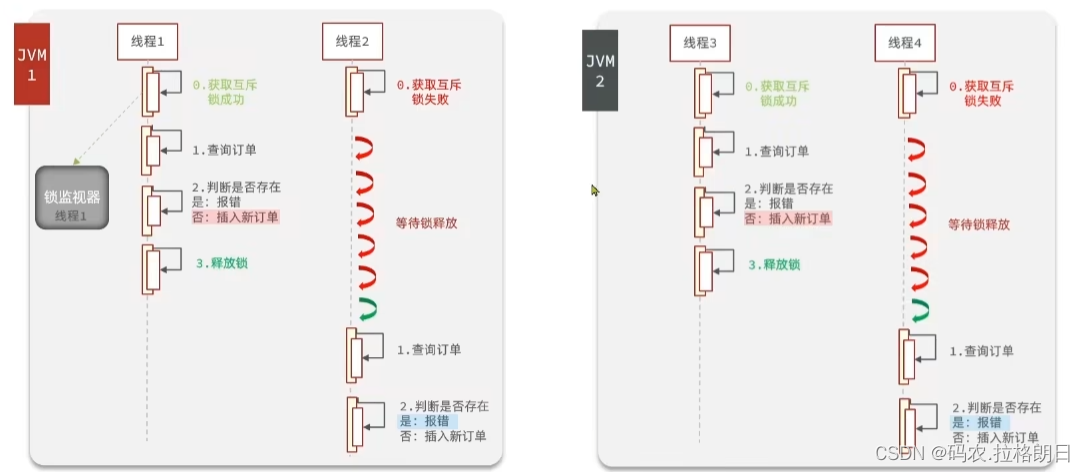
在目标跟踪领域中，需要判断目标之间的距离或相似度，从而判断前后帧的目标是否是同一个目标。

1、距离

常见距离：

• 欧式距离

• 标准化欧式距离

• 马氏距离

• 曼哈顿距离

• 切比雪夫距离

• 闵氏距离

概率分布的距离度量：

• KL散度

• JS距离

• MMD距离

• Principal angle

• HSIC

• Earth Mover’s Distance

本文主要讲解常见距离。

常见距离

2、欧式距离

欧式距离是非常常见和常用的距离度量方式。

欧式距离表示在平面上两点之间直线最短，平面就暗含欧式距离适合二维的情况。

欧式距离是从这些点的笛卡尔坐标用勾股定理计算出来。

公式：

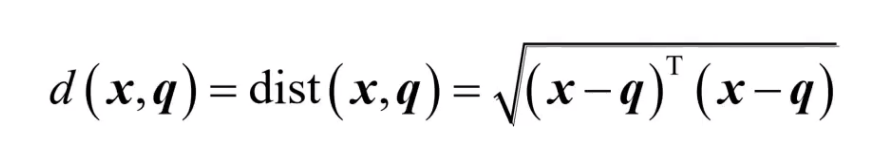
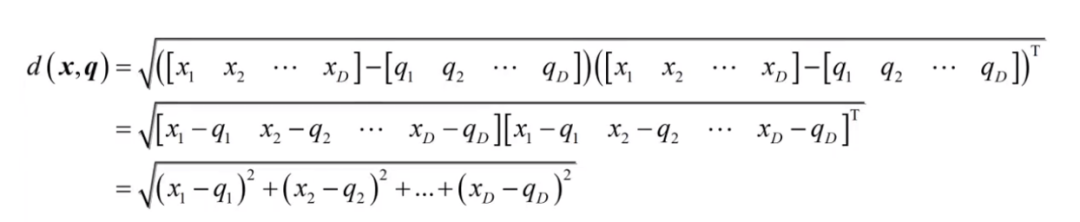
等距线：

正圆

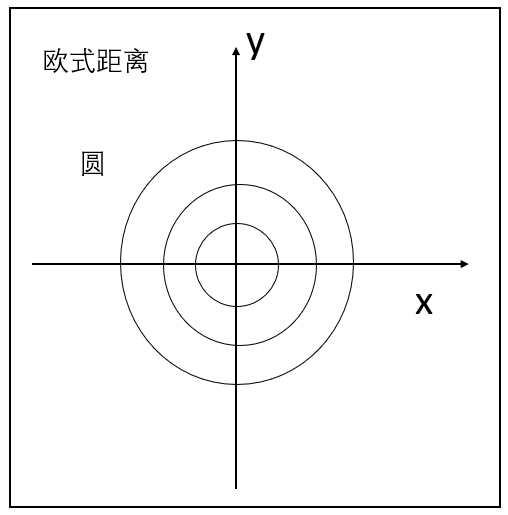
缺点：

尽管欧几里德距离是一种常见的距离度量，但它不是尺度不变的，这意味着计算的距离可能是倾斜的，这取决于特征的单位。

此外，随着数据维度的增加，欧几里得距离就变得不那么有用了。

两大问题：

尺度、单位可能不统一问题：

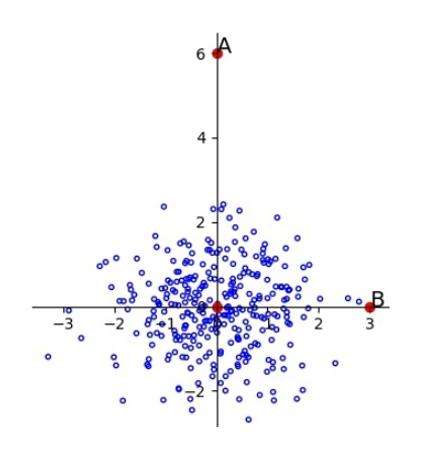
如下图，A  与 B  相对于原点的距离是相同的。但是由于样本总体沿着横轴分布，所以B点更有可能是这个样本中的点，而A则更有可能是离群点。

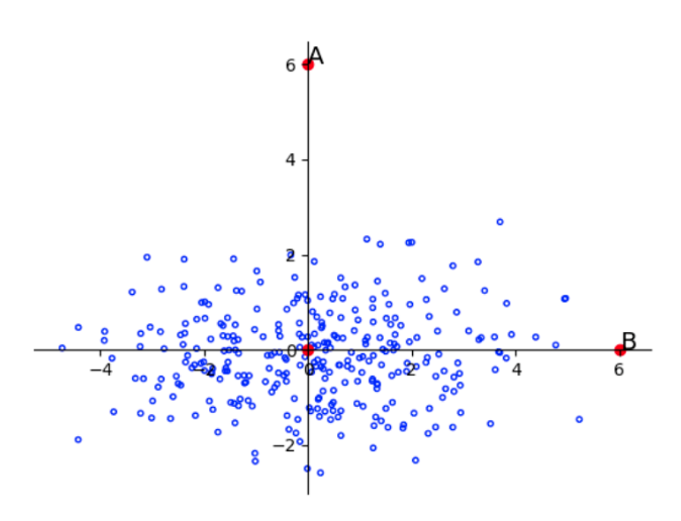
特征之间很可能存在相关性，不是直角问题：

还有一个问题-----如果维度间不独立同分布，样本点一定与欧氏距离近的样本点同类的概率更大吗？

A  与 B  相对于原点的距离依旧相等，显然 A 更像是一个离群点。

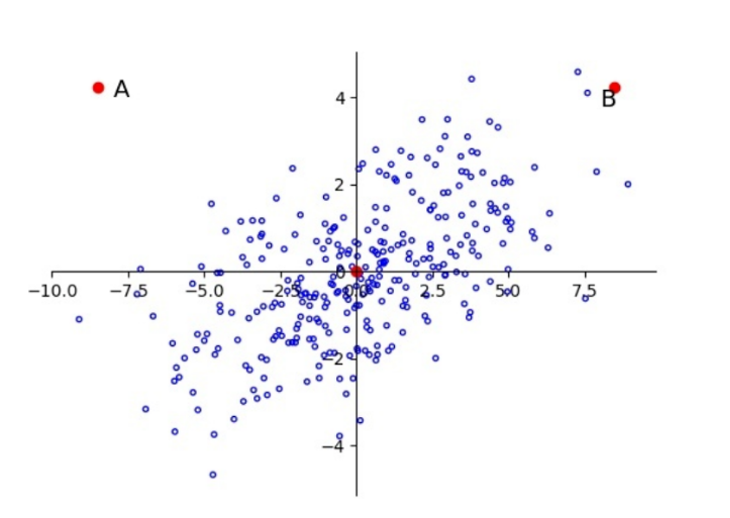
3、标准化欧式距离

为了解决欧式距离尺度不一致的问题，引入了标准化欧式距离。

公式：

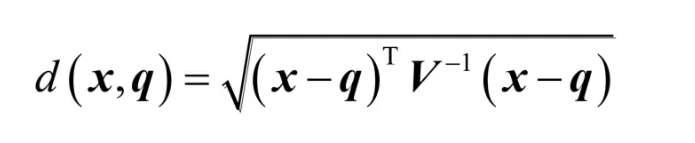
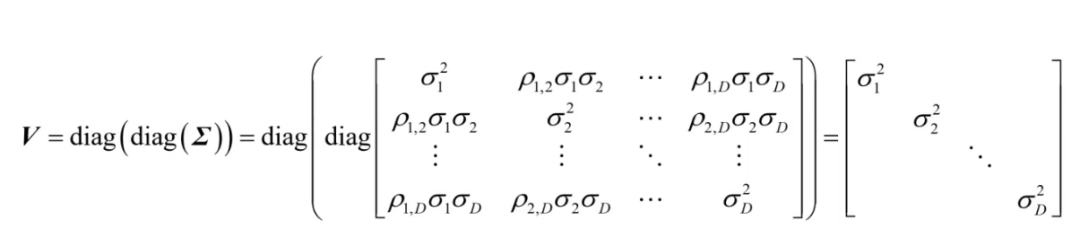
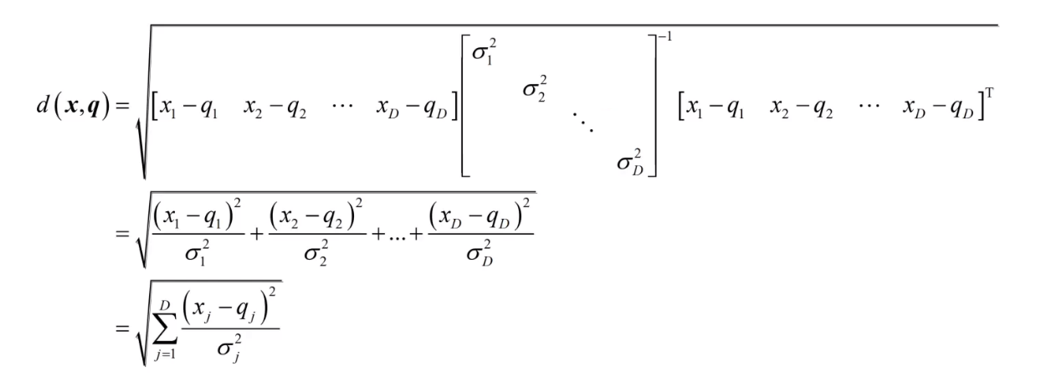
等距线：

正椭圆

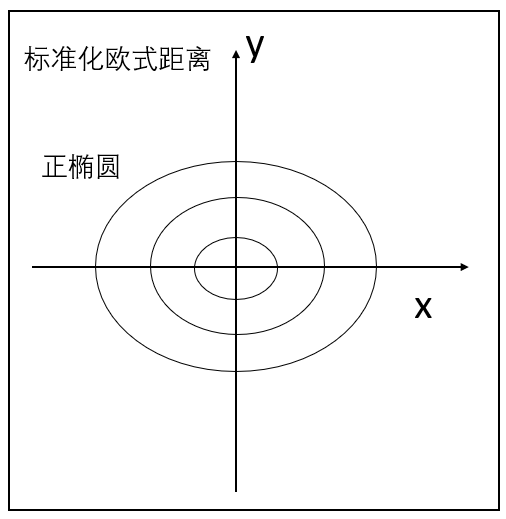
在标准化欧式距离下，x和y可以不同的尺度，换句话说可以根据xy给不同的权重。

而欧式距离相当于xy权重是一样的，1：1的。

4、马氏距离

马氏距离是旋转变换缩放后的欧氏距离。

马氏距离将样本的协方差矩阵纳入距离度量计算，相当于对欧式距离的修正。

马氏距离完成正交，解决了特征间相关性的问题。

马氏距离内含标准化，解决了特征间尺度不一致的问题。

马氏距离可用于判断点到某个分布的距离。

马氏距离是表示数据的协方差距离，计算两个未知样本集的相似度的方法。

由主成分分析可知，由于主成分就是特征向量方向，每个方向的方差就是对应的特征值，所以只需要按照特征向量的方向旋转，然后缩放特征值倍就可以了，得到以下结果：

公式：

马氏距离是旋转变换缩放后的欧氏距离，所以马氏距离的计算公式可以由欧式距离推导而来。

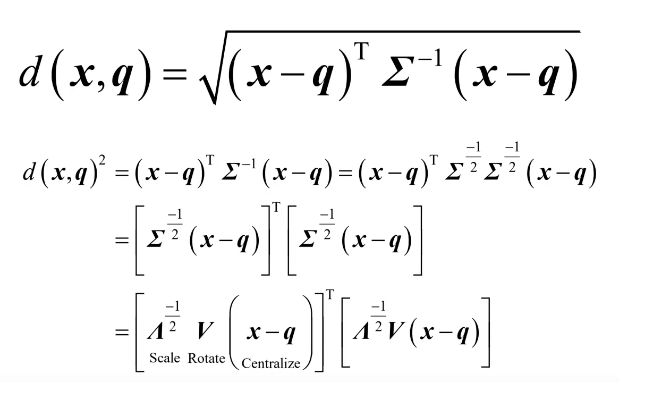
协方差：

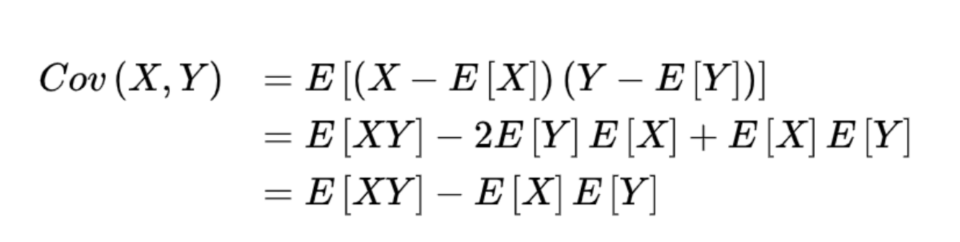
协方差矩阵：

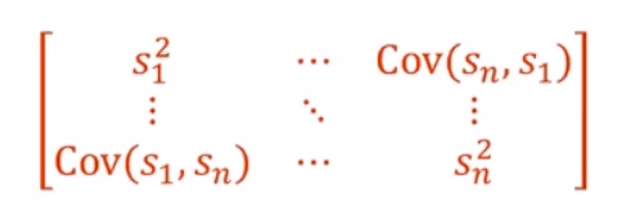
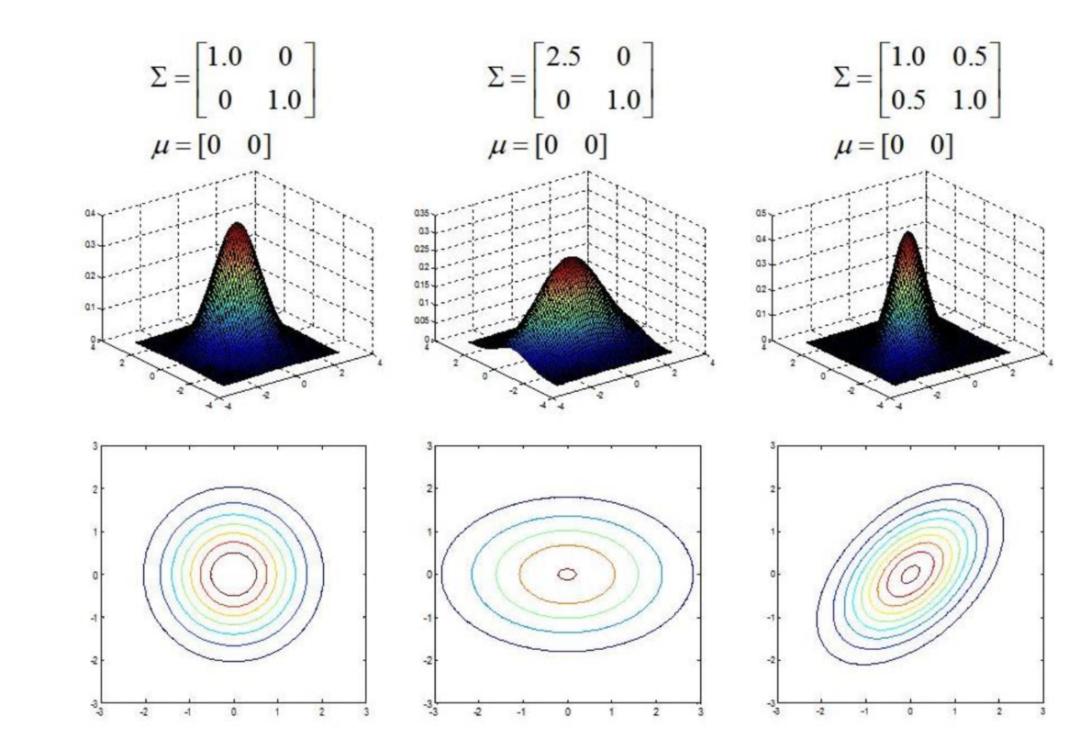
如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离。

欧式距离两个分量的权值都是1，而马氏距离可以是其他值。

等距线:  

旋转椭圆

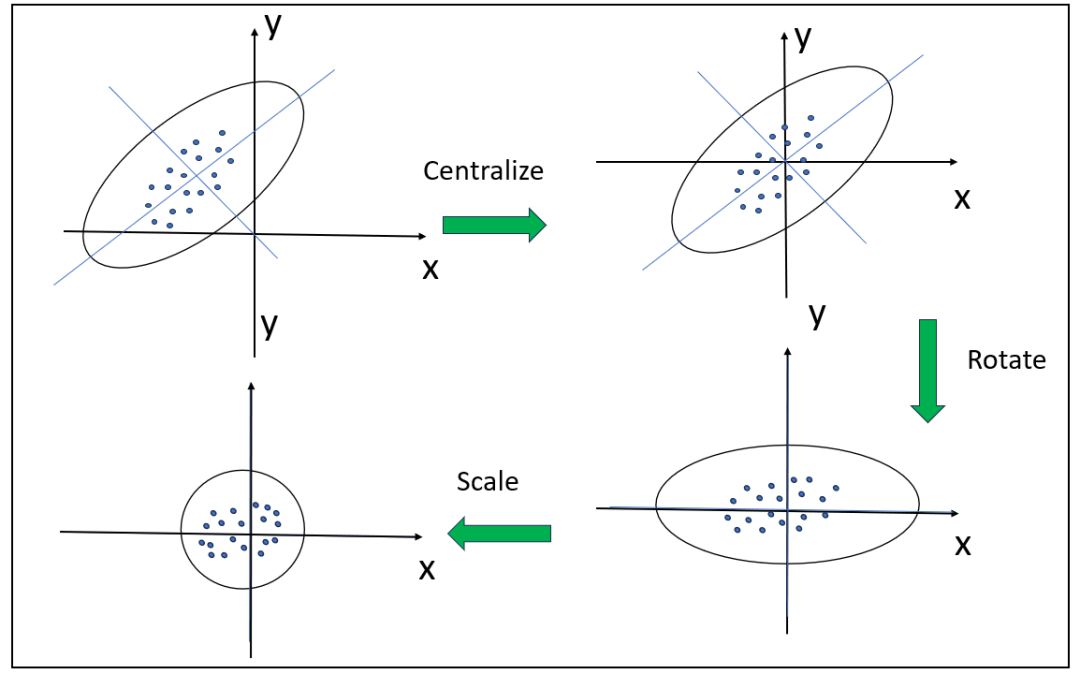
马氏距离，将变量按照主成分进行旋转，让维度间相互独立，然后进行标准化，让维度同分布。

计算样本数据的马氏距离分为两个步骤：

• 坐标旋转

• 数据压缩

坐标旋转的目标：使旋转后的各个维度之间线性无关，所以该旋转过程就是主成分分析的过程。
数据压缩的目标：所以将不同的维度上的数据压缩成为方差都是1的的数据集。

用途：

马氏距离用于异常检测：

马氏距离可用于异常检测，但它于聚类不同，需要先用正常数据计算得到距离数据中心的边界阈值，然后再判别某点距离该数据集中心的位置是否超过该阈值，超过则判定为异常点。

目标跟踪：

需要判断下一帧目标属于哪个目标，可以根据历史数据计算马氏距离判断这个点是不是同一个目标点。

马氏距离的问题：

协方差矩阵必须满秩。

里面有求逆矩阵的过程，不满秩不行，要求数据要有原维度个特征值，如果没有可以考虑先进行PCA，这种情况下PCA不会损失信息

不能处理非线性流形(manifold)上的问题。

只对线性空间有效，如果要处理流形，只能在局部定义。

5、曼哈顿距离

曼哈顿距离，通常称为城市街区距离，计算实值向量之间的距离。

想象描述均匀网格(如棋盘)上物体的向量。曼哈顿距离是指两个矢量之间的距离，如果它们只能移动直角。

在计算距离时不涉及对角线移动。

公式：

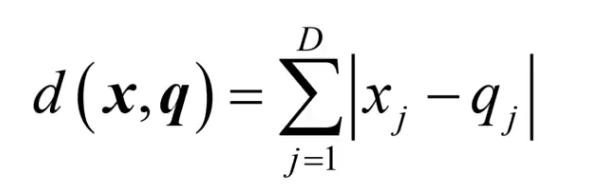
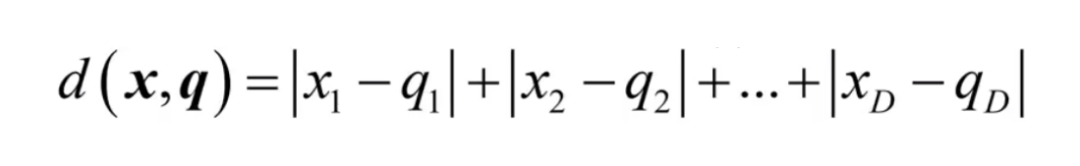
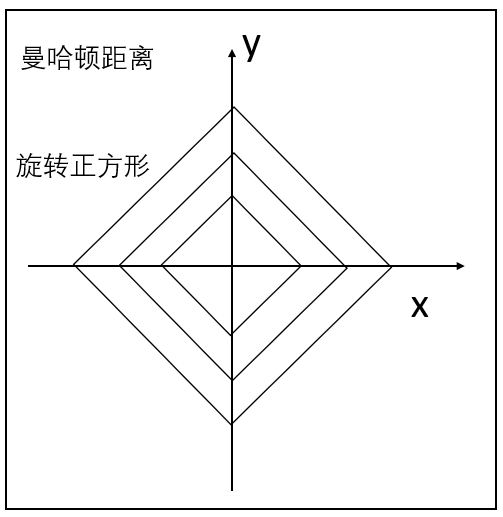
等距线：

旋转正方形

缺点：

尽管曼哈顿距离在高维数据中似乎可以工作，但它比欧几里得距离更不直观，尤其是在高维数据中使用时。

此外，由于它不是可能的最短路径，它比欧几里得距离更有可能给出一个更高的距离值。

6、切比雪夫距离

切比雪夫距离来源于国际象棋，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。

国王从一个格子走到另一个格子最少需要多少步？这个距离就叫切比雪夫距离。

切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。

换句话说，它就是沿着一个轴的最大距离。

公式：

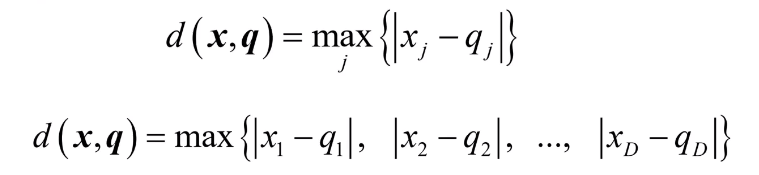
等距线：

正方形

圆心到线段的距离，这个距离代表直线上的其他点到圆心的距离。

即线段上的点距离圆心相等。

或者说取到xy轴的距离的最大值。

在实践中，切比雪夫距离经常用于仓库物流，因为它非常类似于起重机移动一个物体的时间。

另外想到的就是分数分段，各个分段的分数人数多少，看看大多数人集中在哪个分数段。

而看0分到100的总人数就失去了意义。

7、闵式距离

闵氏距离是一系列距离的集合。

公式：

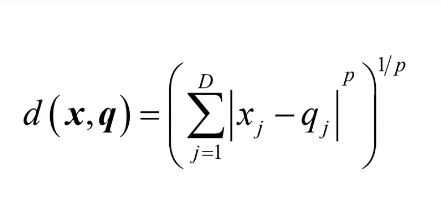
p=1，城市街区距离

p=2，欧式距离

p=+∞，切比雪夫距离

等距线：

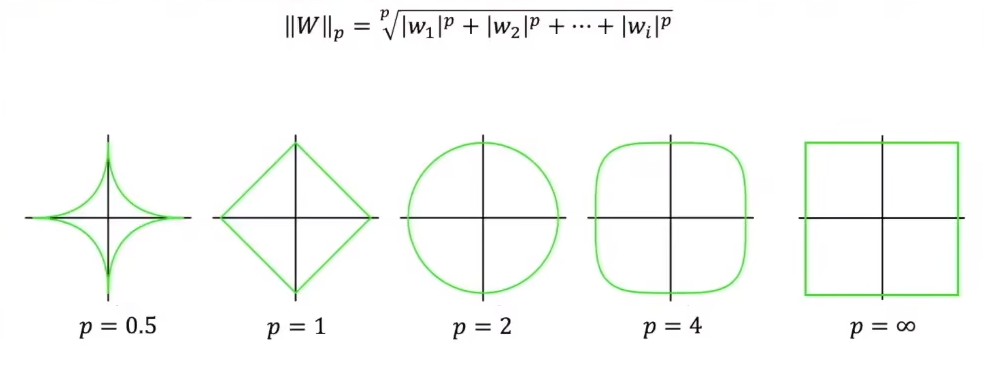
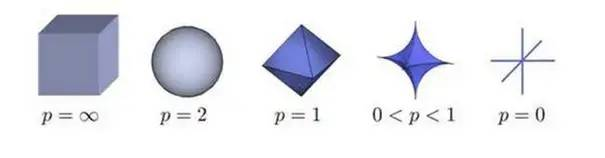
（灵魂拷问：闵氏距离p->∞,转变成切比雪夫距离。问题是上面的公式求极限，怎么就得出下面的max的呢？）

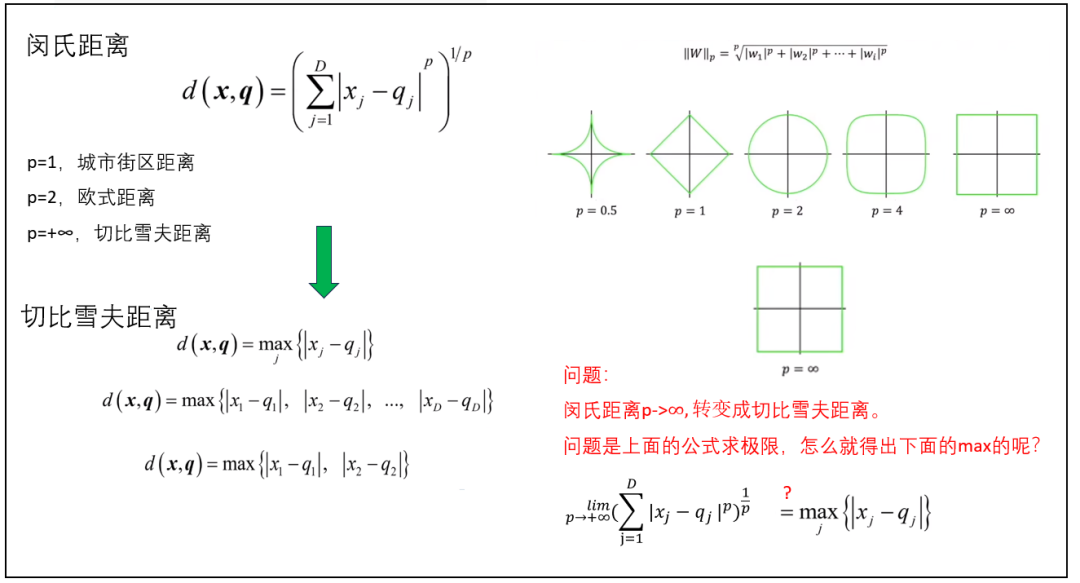
证明：

8、总结

空间：欧氏距离

路径：曼哈顿距离 国际象棋国王：切比雪夫距离 （以上三种的统一形式:闵可夫斯基距离）

加权：标准化欧氏距离

排除量纲和依存：马氏距离

向量差距：夹角余弦

编码差别：汉明距离

集合近似度：杰卡德相似系数与距离

相关：相关系数与相关距离

时间序列：DTW距离

 ——————

浅谈则止，细致入微AI大道理

扫描下方“AI大道理”，选择“关注”公众号

—————————————————————

 

—————————————————————

投稿吧   | 留言吧