文章目录
- 目标
- 原理
- 设计与实现(代码快照以及代码)
- 运行界面和结果截图
- 结语
目标
给定一个距离矩阵,利用 Floyd– Warshall 算法编程(C语言)求任意两点之间的最短距离。
原理
求取多源最短路径常用Floyd算法,通过对比直达距离和从各点中转距离之和相比,若采用中转的方式比直达距离短,则其就为当前最短路径。如:从地方A到地方B距离为5,A到C距离为2,C到B距离为2,在这种情况下可以从C中转到B,最短距离就是2 + 2 = 4。Floyd核心算法如下:
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
for (int k = 0; k < 4; k++)
{
if (matrix[i][j] > matrix[i][k] + matrix[k][j])
{
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
}
设计与实现(代码快照以及代码)
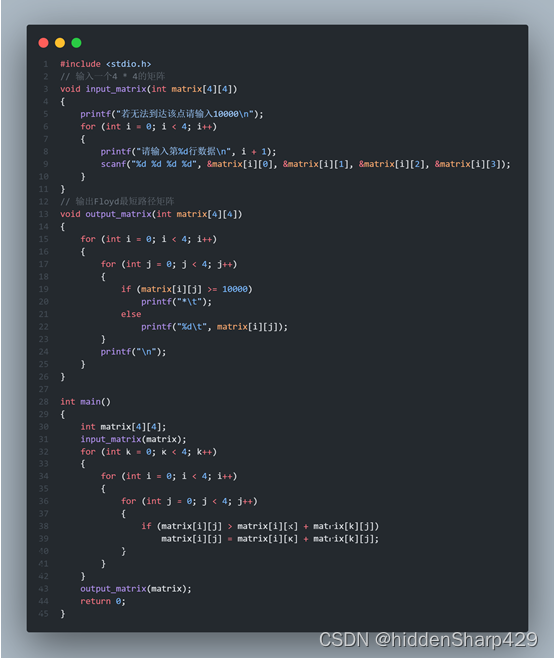
#include <stdio.h>
// 输入一个4 * 4的矩阵
void input_matrix(int matrix[4][4])
{
printf("若无法到达该点请输入10000\n");
for (int i = 0; i < 4; i++)
{
printf("请输入第%d行数据\n", i + 1);
scanf("%d %d %d %d", &matrix[i][0], &matrix[i][1], &matrix[i][2], &matrix[i][3]);
}
}
// 输出Floyd最短路径矩阵
void output_matrix(int matrix[4][4])
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
if (matrix[i][j] >= 10000)
printf("*\t");
else
printf("%d\t", matrix[i][j]);
}
printf("\n");
}
}
int main()
{
int matrix[4][4];
input_matrix(matrix);
for (int k = 0; k < 4; k++)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
if (matrix[i][j] > matrix[i][k] + matrix[k][j])
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
output_matrix(matrix);
return 0;
}
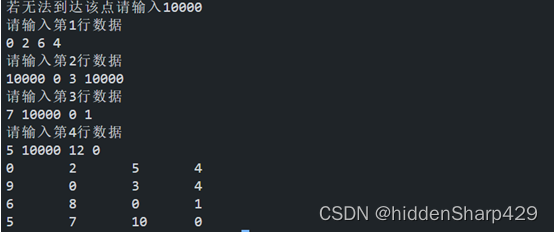
运行界面和结果截图
原矩阵
0
2
6
4
∞
0
3
∞
7
∞
0
1
5
∞
12
0
\begin{matrix} &0 &2 &6 &4 \\ &\infty &0 &3 &\infty \\ &7 &\infty &0 &1 \\ &5 &\infty &12 &0\\ \end{matrix}
0∞7520∞∞630124∞10
经过Floyd算法计算后的矩阵
0
2
5
4
9
0
3
4
6
8
0
1
5
7
10
0
\begin{matrix} &0 &2 &5 &4 \\ &9 &0 &3 &4 \\ &6 &8 &0 &1 \\ &5 &7 &10 &0\\ \end{matrix}
09652087530104410
结语
如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!
参考文献:只有五行的Floyd最短路径算法