作者主页:paper jie的博客_CSDN博客-C语言,算法详解领域博主
本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。
本文录入于《算法详解》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造,将算法基础知识一网打尽,希望可以帮到读者们哦。
其他专栏:《系统解析C语言》《C语言》《C语言-语法篇》
内容分享:本期将对求最小公倍数和最大公因数进行详细的讲解,各位看官姥爷快搬好小板凳坐好叭。
-------- 不要998,不要98,只要一键三连,三连买不了吃亏,买不了上当
目录
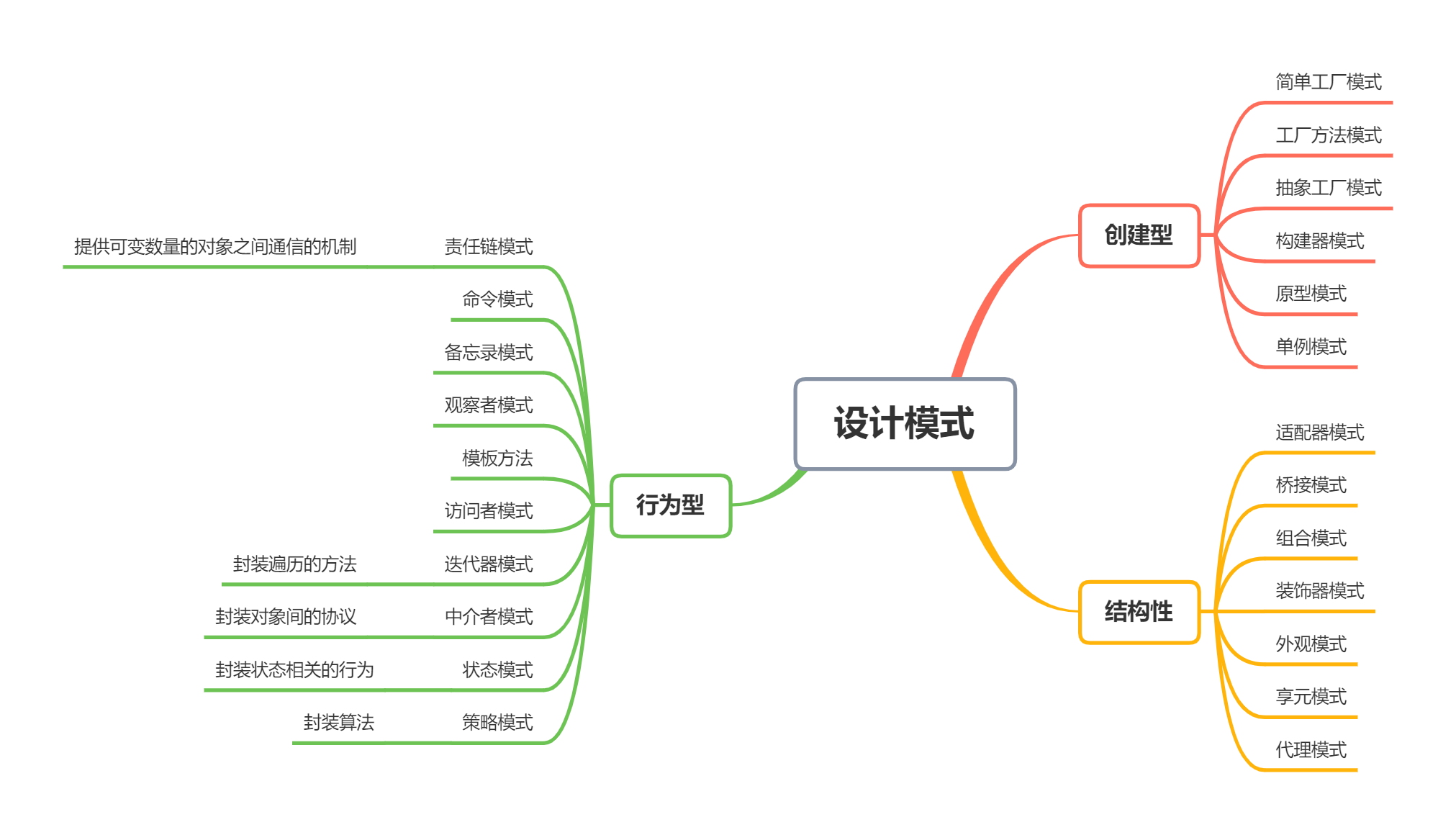
最大公约数和最小公倍数的定义
实现的基本思想
具体代码
最大公约数和最小公倍数的定义
如果数a能被数b整除,a就叫做b的倍数,b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系,不能单独存在。如只能说16是某数的倍数,2是某数的约数,而不能孤立地说16是倍数,2是约数。最大公约数就是最大的约数。公倍数是指在两个或两个以上的 自然数 中,如果它们有相同的 倍数 ,这些倍数就是它们的公倍数。 公倍数中最小的,就称为这些 整数 的 最小公倍数
实现的基本思想
求最大公因数我们采用辗转相除法。什么是辗转相除法呢?
在数学中,辗转相除法,又称欧几里得算法,是求取最大公约数的一种算法。辗转相除法首次出现于欧几里得的《几何原本》中的第Ⅶ卷,书中的命题ⅰ和命题ⅱ所描述的就是辗转相除法,而在中国,辗转相除法最早出现在《九章算法》中。它有一个经典的几何描述:
辗转相除法既然起源于希腊,那么就从希腊开始讲起,希腊人非常喜欢从图形或者说是用几何的角度去看待问题,很多问题希腊数学家都习惯先去思考能否将其转化为直观的几何问题再进行求解,希腊数学家甚至认为:所有的数字都与一个几何概念有关系。我们今天所说的「有理数」和「无理数」这两个概念,英文是将其翻译成「Rational number」和「Irrantional number」的,而这两个单词的拉丁文词源(Ratio)的原意则是成比例的意思。所以很自然地,希腊数学家在面对求两数的最大公约数这个问题的时候,也首先去思考这个问题是否能通过将其转化成一个几何问题来处理。在经过一些尝试之后,这一设想最终实现了,希腊数学家是这样处理的,将所要求取最大公约数的两个数字A、B分别作为矩形的两条边,就形成了一个矩形,这样,原来的问题就被转化了。
还记得最大公约数的定义吗?所谓最大公约数,就是指两个数字所共同拥有的约数中最大的那一个。这种描述是以数字的方式进行描述的,这种数字形式的描述太过抽象,使人不好理解,因为人类数十万年来的生活导致人类的认知方式会更偏向於图形这种更加直观的方式。那么现在问题就变成了:如何将最大公约数问题从用数字进行描述,转化为图形或者说几何形式的描述。希腊数学家是这样处理的,即:以所要求取最大公约数的两个数字为边构造一个矩形,然后尝试在这个矩形中去找到这样一个正方形,这类正方形能够没有缝隙的铺满上述矩形,很明显,这类正方形有很多个的(这里只考虑正整数边长),而我们的目标就是找出这类正方形中最大的那一个。所以问题现在就又转化成了:该怎么找到这样一个正方形?
希腊数学家是这样处理的,在我们预先构造的矩形中,我们先以矩形的短边构造正方形,然后再去计算这样的正方形可以在大矩形中「最多」放置多少个,这个计算过程可以用取余的方式进行计算。接下来,我们再用长边余下的长度构建正方形,在去试图铺满剩下未被覆盖的部分,然后计算这个正方形最多可以放置几个,直到我们找到这样一个正方形,这个正方形可以完全铺满整个大矩形。那么这个正方形就是我们最终要找的答案,自然而然的,这个正方形的边长也就是我们要找的两数的最大公约数。
辗转相除法之所以有效是因为其基于一个核心原理,即:两个数的最大公约数等于其中较小的数字和二者之间余数的最大公约数为了更容易理解,可以对这句话进行简单的分析,以m和n举例:m%n!=0的话,将n的值赋给m,m%n的余数赋给n。这样是一次循环,后面一直循环以上步骤直到m%n==0,这时n里面的值就是最大公因数。
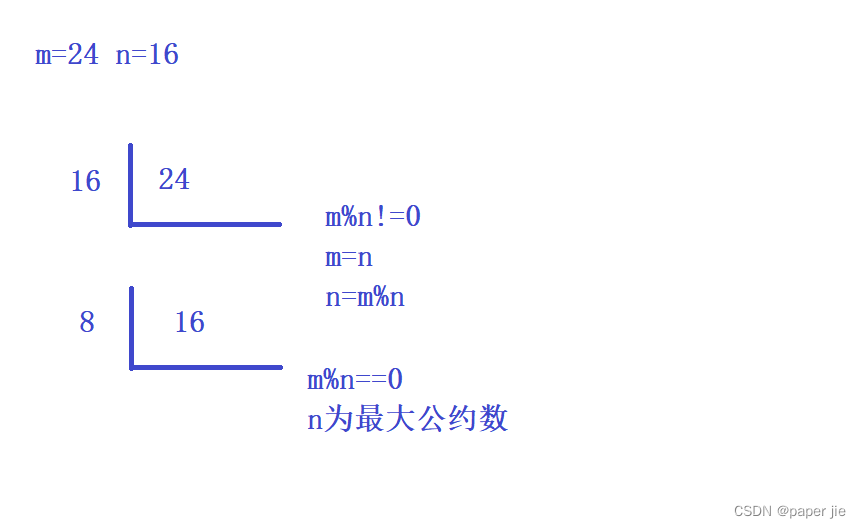
求最小公倍数我们可以用一个公式:m*n/最大公因数
因为 最大公因数*最小公倍数 = m * n,所以我们知道其中一个就可以求出另一个了。
具体代码
注意:这里m和n的大小其实不用纠结,因为m%n时它们的位置就会变的正常,比如:m=2 n=3 它们一旦采用辗转相除法,就会变成m=3 n=2.
int main()
{
int m = 0;
int n = 0;
//要输入的值
scanf("%d %d", &m, &n);
//用a b另存一份m n的值,等下求最小公倍数可以用
int a = m;
int b = n;
//m%n==0 时跳出
while (m % n != 0)
{
int tmp = m % n;
m = n;
n = tmp;
}
printf("最大公因数=%d\n", n);
//最大公约数*最小公倍数=m*n
//知一个就可以求另一个
printf("最小公倍数=%d\n", a * b / n);
return 0;
}