【动态规划算法】第八题：931.下降路径最小和

news2024/11/16 17:55:32

💖作者：小树苗渴望变成参天大树🎈
🎉作者宣言：认真写好每一篇博客💤
🎊作者gitee:gitee✨
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法\🎄

如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言

前言

hello，大家好，我们今天开始讲动态规划的第八题，这个题目相比较前面来说，再dp表上有了一点小变化，中间我会给大家讲解为什么要这么做，话不多说，我们开始进入正文

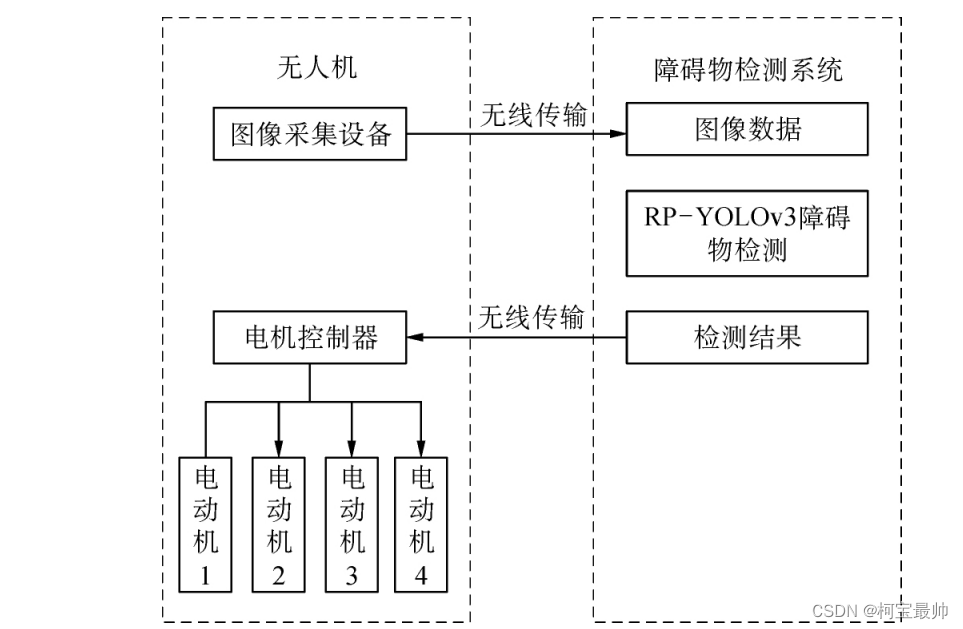
第八个题目是下降路径最小和

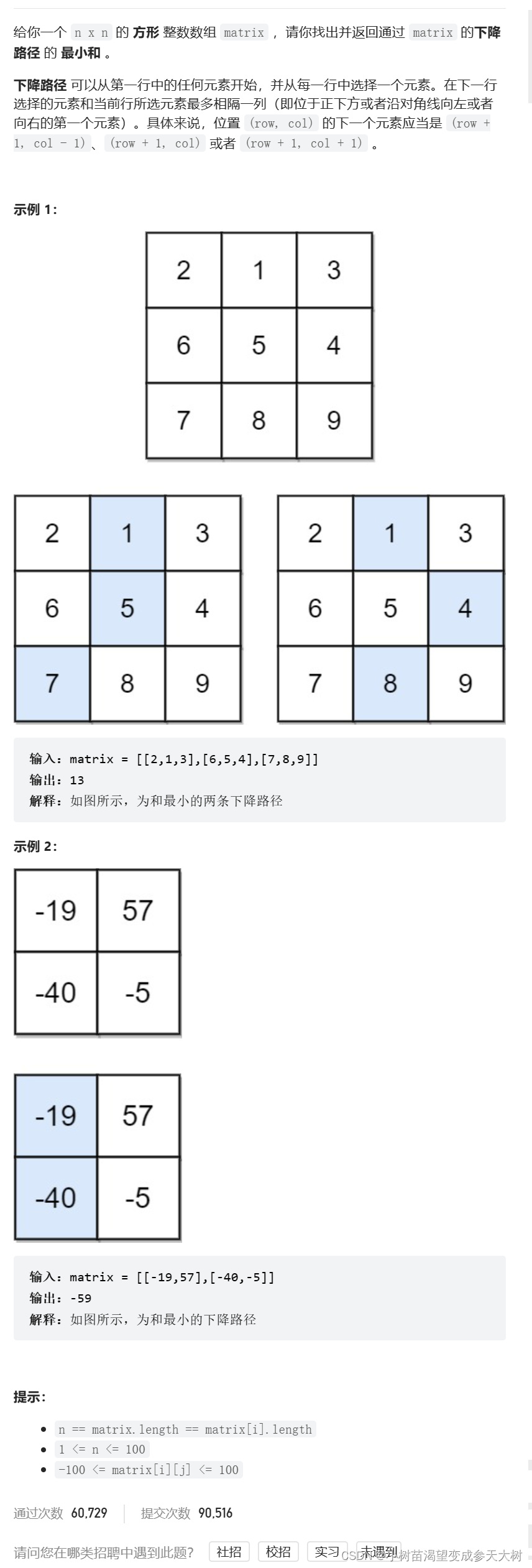
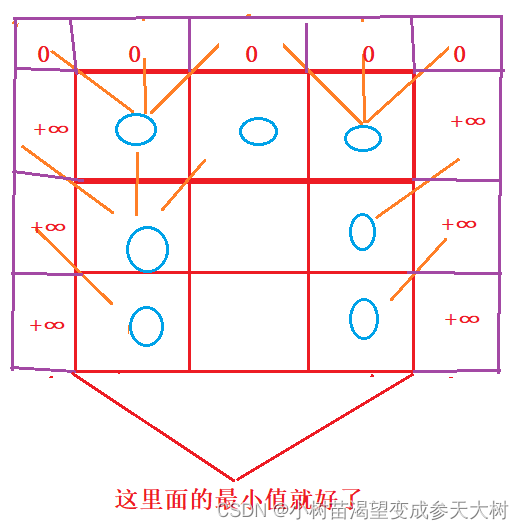
在这里插入图片描述

通过图解来看题目解析：

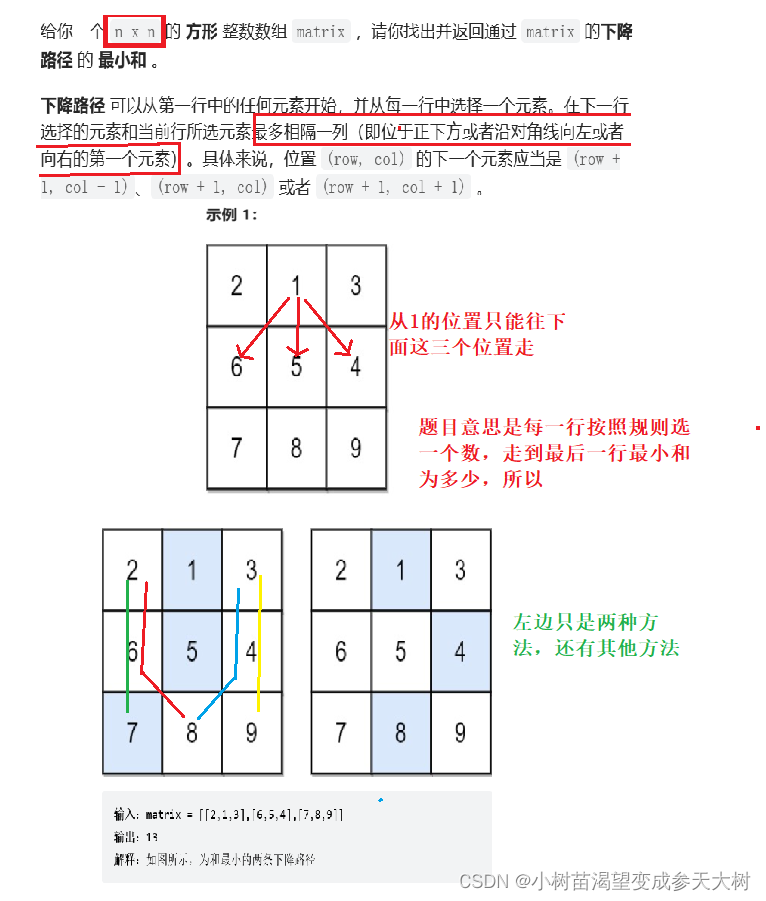
在这里插入图片描述

接下来用动态规划的步骤给大家讲解：

状态表示：经验+题目要求
以(i,j)位置为终点，dp[i][j]表示到达(i,j)位置的最小和
状态转移方程：以最近状态算此状态的值

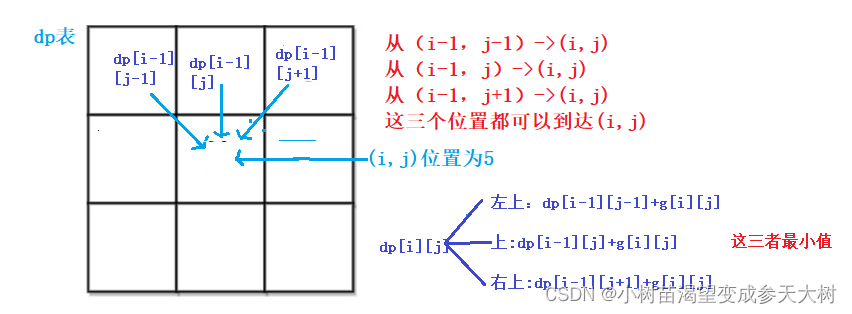
dp[i][j]=min(x,y,z);
初始化：保证数组不越界
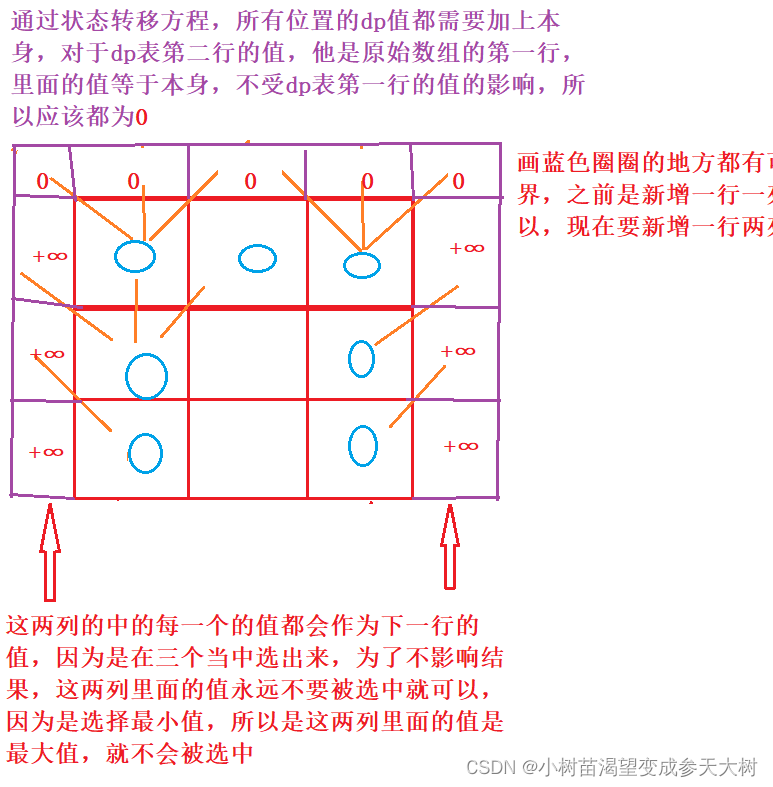
填表顺序：因为是通过上面一行选择下面的值，和左右没啥关系，所以填表顺序是从上往下，每一行随便
返回值，根据题目要求，我们要选择出到达最低一行的最小值，而dp表的最后一行是达到最后一行位置的最小值，这些任意位置的最小值互相比较才是我们到达最后一行的最小，所以返回值为：min(dp[n][i]);

代码实现：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        //1.创建dp表
        int n=matrix.size();
        vector<vector<int>> dp(n+1,vector<int>(n+2,INT_MAX));//先将dp表都初始化为正无穷
         //2.初始化
        for(int i=0;i<=n+1;i++)dp[0][i]=0;//再把第一行变成0
       //3.填表
       for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))
                        +matrix[i-1][j-1];

        int ret=dp[n][1];
        for(int j=1;j<=n;j++)
            ret=min(ret,dp[n][j]);

        return ret;
    }
}

这题的初始化非常巧妙，如果大家不理解，可以再填表的时候讲最左边和最右边的两种情况加一个判断，来看代码：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        //1.创建dp表 
        int n=matrix.size();
        vector<vector<int>> dp(n+1,vector<int>(n+1));
        //特殊情况
        if(n==1)return matrix[n-1][n-1];
        //3.填表
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(j==1)
                {
                    dp[i][j]=min(dp[i-1][j],dp[i-1][j+1])+matrix[i-1][j-1];//上和右上
                }
                else if(j==n)
                {
                    dp[i][j]=min(dp[i-1][j],dp[i-1][j-1])+matrix[i-1][j-1];//上和左上
                }
                else
                {
                    dp[i][j]=min(dp[i-1][j],min(dp[i-1][j+1],dp[i-1][j-1]))+matrix[i-1][j-1];//三个方向
                }
            }
        }
        int min=dp[n][1];
        for(int i=1;i<=n;i++)
        {
            if(dp[n][i]<=min)
            {
                min=dp[n][i];
            }
        }
      
        //4.返回值
         return min;
    }
};