专注效率记忆
预习笔记复习做题

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

本博客带大家一起学习，我们不图快，只求稳扎稳打。
由于我高三是在家自学的，经验教训告诉我，学习一定要长期积累，并且复习，所以我推出此系列。
只求每天坚持40分钟，一周学5天，复习2天
也就是一周学10道题
60天后我们就可以学完81道题，相信60天后，我们一定可以有扎实的代码基础！我们每天就40分钟，和我一起坚持下去吧！
qq群：878080619

第七天【考研408-数据结构（笔试）】

五、表达式求值
- 1. 表达式求值
六、树的遍历（递归）
- 1. 二叉树的带权路径长度
- 2. 重建二叉树
- - - 构建二叉树的两种情况
七、二叉搜索树与表达式树
- 1. 二叉排序树（中序遍历是有序的）
- 2. 表达式树
八、Huffman树
- 1. 合并果子
- 2. 荷马史诗
- - - 考点：（构建深度最小的哈夫曼树）利用pair
    - 考点：（ k进制哈夫曼树需要补零节点）

五、表达式求值

1. 表达式求值

在这里插入图片描述

#include <iostream>
#include <stack>
#include <string>
#include <unordered_map>
using namespace std;

stack<int> num;
stack<char> op;

//优先级表
unordered_map<char, int> h{ {'+', 1}, {'-', 1}, {'*',2}, {'/', 2} };


void eval()//求值
{
    int a = num.top();//第二个操作数
    num.pop();

    int b = num.top();//第一个操作数
    num.pop();

    char p = op.top();//运算符
    op.pop();

    int r = 0;//结果 

    //计算结果
    if (p == '+') r = b + a;
    if (p == '-') r = b - a;
    if (p == '*') r = b * a;
    if (p == '/') r = b / a;

    num.push(r);//结果入栈
}

int main()
{
    string s;//读入表达式
    cin >> s;

    for (int i = 0; i < s.size(); i++)
    {
        if (isdigit(s[i]))//数字入栈
        {
            int x = 0, j = i;//计算数字
            while (j < s.size() && isdigit(s[j]))
            {
                x = x * 10 + s[j] - '0';
                j++;
            }
            num.push(x);//数字入栈
            i = j - 1;
        }
        //左括号无优先级，直接入栈
        else if (s[i] == '(')//左括号入栈
        {
            op.push(s[i]);
        }
        //括号特殊，遇到左括号直接入栈，遇到右括号计算括号里面的
        else if (s[i] == ')')//右括号
        {
            while(op.top() != '(')//一直计算到左括号
                eval();
            op.pop();//左括号出栈
        }
        else
        {
            while (op.size() && h[op.top()] >= h[s[i]])//待入栈运算符优先级低，则先计算
                eval();
            op.push(s[i]);//操作符入栈
        }
    }
    while (op.size()) eval();//剩余的进行计算
    cout << num.top() << endl;//输出结果
    return 0;
}

六、树的遍历（递归）

1. 二叉树的带权路径长度

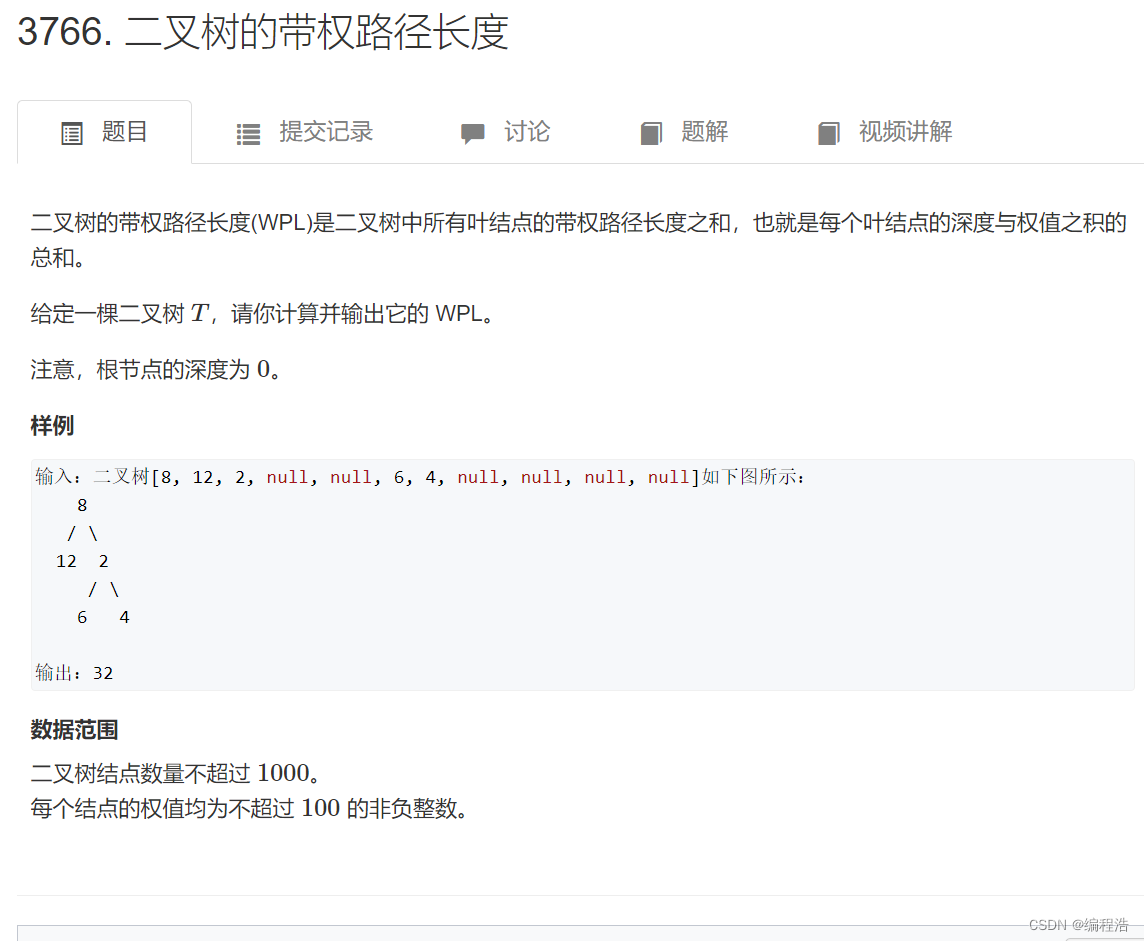
在这里插入图片描述

class Solution {
public:
    int sum(TreeNode* root, int level) {
        if(!root) return 0;
        if(!root->left && !root->right) {
            return root->val * level;
        }
        return sum(root->left, level + 1) + sum(root->right, level + 1);
    }

    int pathSum(TreeNode* root) {
        return sum(root, 0);
    }
};

2. 重建二叉树

构建二叉树的两种情况

构建二叉树的两种情况【根据前序遍历和中序遍历构造树】【根据后序遍历和中序遍历构造树】
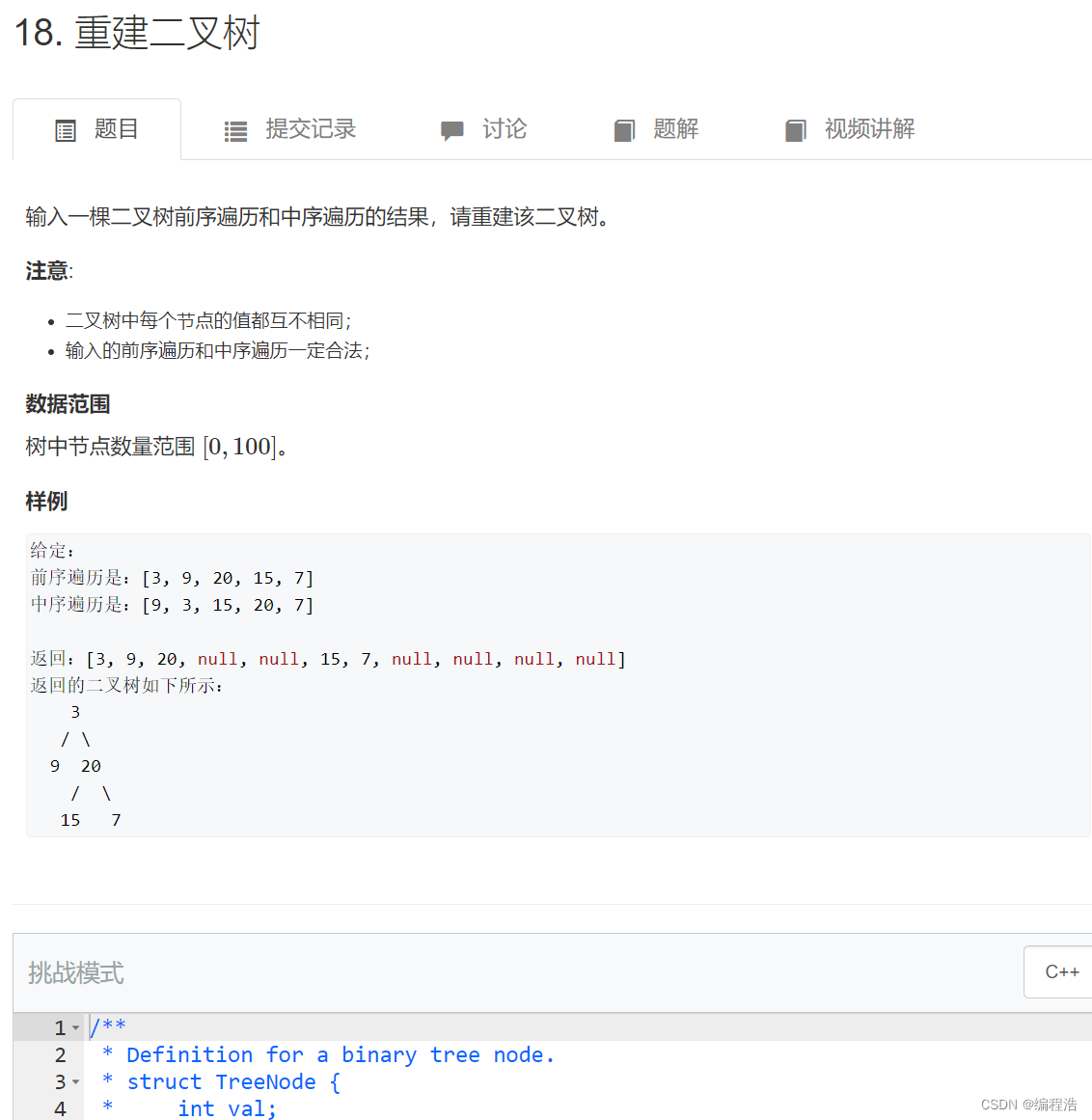
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    unordered_map<int,int> pos;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for (int i = 0; i < n; i ++ )
            pos[inorder[i]] = i;
        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
    {
        if (pl > pr) return NULL;
        int k = pos[pre[pl]] - il;
        TreeNode* root = new TreeNode(pre[pl]);
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }
};

七、二叉搜索树与表达式树

1. 二叉排序树（中序遍历是有序的）

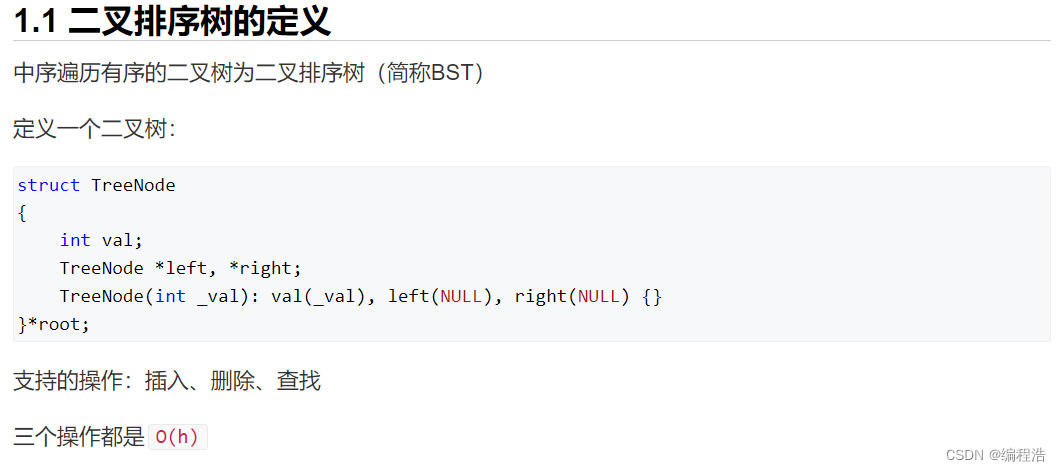
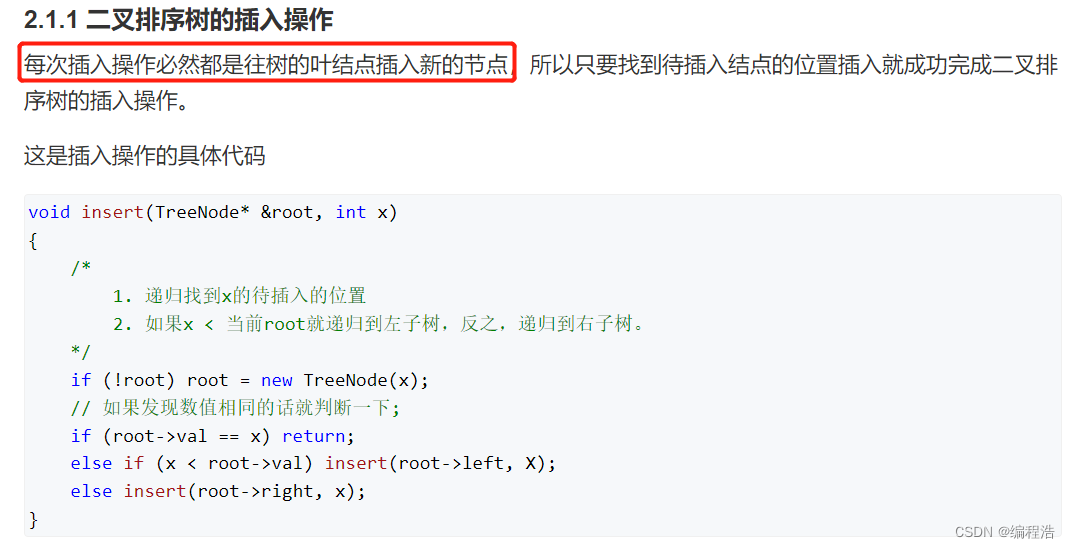
在这里插入图片描述

解释一下删除操作的第三点：

首先我们要清楚：
二叉排序树的特点是
中序遍历（左根右）是有序的

所以如果删除的根节点有左右子树

那么我们为了保证有序

就要把根节点左子树的最右边赋值给根节点
因为根节点左子树的最右边是比根节点小中最大的点

只有这样才能保证删除根节点后

左子树比新的根节点都小
右子树比新的根节点都大

#include <bits/stdc++.h>

using namespace std;

const int INF = 2e9;

struct TreeNode
{
    int val;
    TreeNode *left, *right;
    TreeNode(int _val): val(_val), left(NULL), right(NULL) {}
}*root;

// 插入操作
void insert(TreeNode* &root, int x)
{
    /*
        1. 递归找到x的待插入的位置
        2. 如果x < 当前root就递归到左子树，反之，递归到右子树。
    */ 
    if (!root) root = new TreeNode(x);
    // 如果发现数值相同的话就判断一下;
    if (root->val == x) return;
    else if (x < root->val) insert(root->left, x);
    else insert(root->right, x);
}

void remove(TreeNode* &root, int x)
{
    /*
        1. 待删除的结点只有左子树。立即可推出，左子树上的结点都是小于待删除的结点的，我们只需要把待删除结点删了然后左子树接上待删除结点的父节点就可以了。
        2. 待删除的结点只有右子树。立即可推出，右子树上的结点都是大于待删除的结点的，我们只需要把待删除结点删了然后右子树接上待删除结点的父节点就可以了。
        3. 待删除的结点既有左子树又有右子树。这个比上两个情况麻烦一点，但也不麻烦，需要读者理解的是，怎么能删除结点后还不改变中序遍历的结果，并且操作代价最小，显而易见，我们根据待删除结点的左子树可以得到最右下角的最后结点满足$<x$并且最接近x的结点，把这个结点覆盖待删除的结点，然后把这个结点删除，就完成了我们的操作。
    */

    // 如果不存在直接return
    if (!root) return;
    if (x < root->val) remove(root->left, x);
    else if (x > root->val) remove(root->right, x);
    else
    {
        if (!root->left && !root->right) root = NULL;
        else if (!root->left) root = root->right;
        else if (!root->right) root = root->left;
        else
        {
            auto p = root->left;
            while (p->right) p = p->right;
            root->val = p->val;
            remove(root->left, p->val);
        }
    }
}

// 输出数值 x 的前驱(前驱定义为现有所有数中小于 x 的最大的数)。
int get_pre(TreeNode* root, int x)
{
    if (!root) return -INF;
    if (root->val >= x) return get_pre(root->left, x);
    else return max(root->val, get_pre(root->right, x));
}

// 输出数值 x 的后继(后继定义为现有所有数中大于 x 的最小的数)。
int get_suc(TreeNode* root, int x)
{
    if (!root) return INF;
    if (root->val <= x) return get_suc(root->right, x);
    else return min(root->val, get_suc(root->left, x));
}

int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int t, x;
        cin >> t >> x;
        if (t == 1) insert(root, x);
        else if (t == 2) remove(root, x);
        else if (t == 3) cout << get_pre(root, x) << endl;
        else cout << get_suc(root, x) << endl;
    }
    return 0;
}

2. 表达式树

本题就是中序遍历
只要不是叶子节点
就加左括号然后遍历左边
遍历完右边加右括号

在这里插入图片描述

class Solution {
public:
    string dfs(TreeNode* root) {
        if(!root) return "";
        if(!root->left && !root->right) {
            return root->val;
        }
        string ret = "";
        ret += '(';
        ret += dfs(root->left);
        ret += root->val;
        ret += dfs(root->right);
        ret += ')';
        return ret;
    }

    string expressionTree(TreeNode* root) {
        return dfs(root->left) + root->val + dfs(root->right);
    }
};

八、Huffman树

1. 合并果子

在这里插入图片描述
什么是哈夫曼树

本题就记住哈夫曼树的最简代码如下：

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    priority_queue<int, vector<int>, greater<int>> heap;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        heap.push(x);
    }

    int res = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        res += a + b;
        heap.push(a + b);
    }

    printf("%d\n", res);
    return 0;
}

2. 荷马史诗

考点：（构建深度最小的哈夫曼树）利用pair

可以忽略这个段，下面有
图中所说的合并的次数，本质其实是根节点的深度
所以优先队列的元素是pair<long long ,int>
一个记录权值一个记录深度

考点：（ k进制哈夫曼树需要补零节点）

题解图中有解释
原题链接

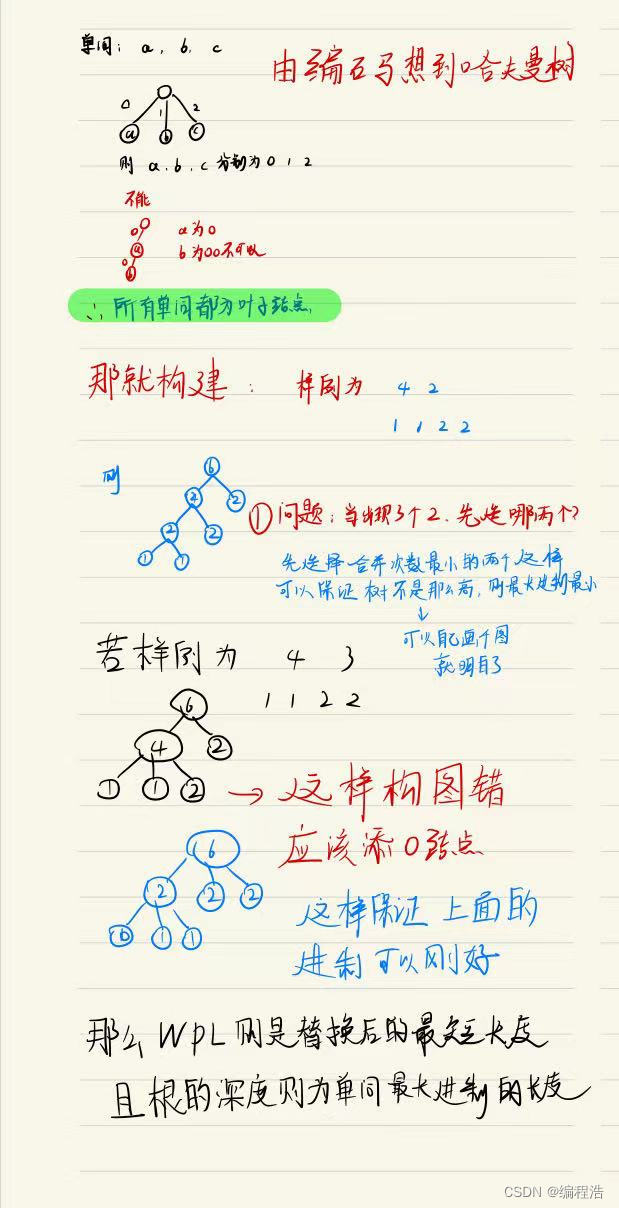
在这里插入图片描述

图中所说的合并的次数，本质其实是根节点的深度

所以优先队列的元素是pair<long long ,int>
一个记录权值一个记录深度

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<LL, int> PLI;

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    priority_queue<PLI, vector<PLI>, greater<PLI>> heap;
    while (n -- )
    {
        LL w;
        scanf("%lld", &w);
        heap.push({w, 0});
    }
    while ((heap.size() - 1) % (k - 1)) heap.push({0, 0});

    LL res = 0;
    while (heap.size() > 1)
    {
        LL s = 0;
        int depth = 0;
        for (int i = 0; i < k; i ++ )
        {
            auto t = heap.top();
            heap.pop();
            s += t.x, depth = max(depth, t.y);
        }
        heap.push({s, depth + 1});
        res += s;
    }

    printf("%lld\n%d\n", res, heap.top().y);
    return 0;
}