视频课程：从此再也不怕动态规划了，动态规划解题方法论大曝光 ！| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili

DP概念以及和贪心的区别

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

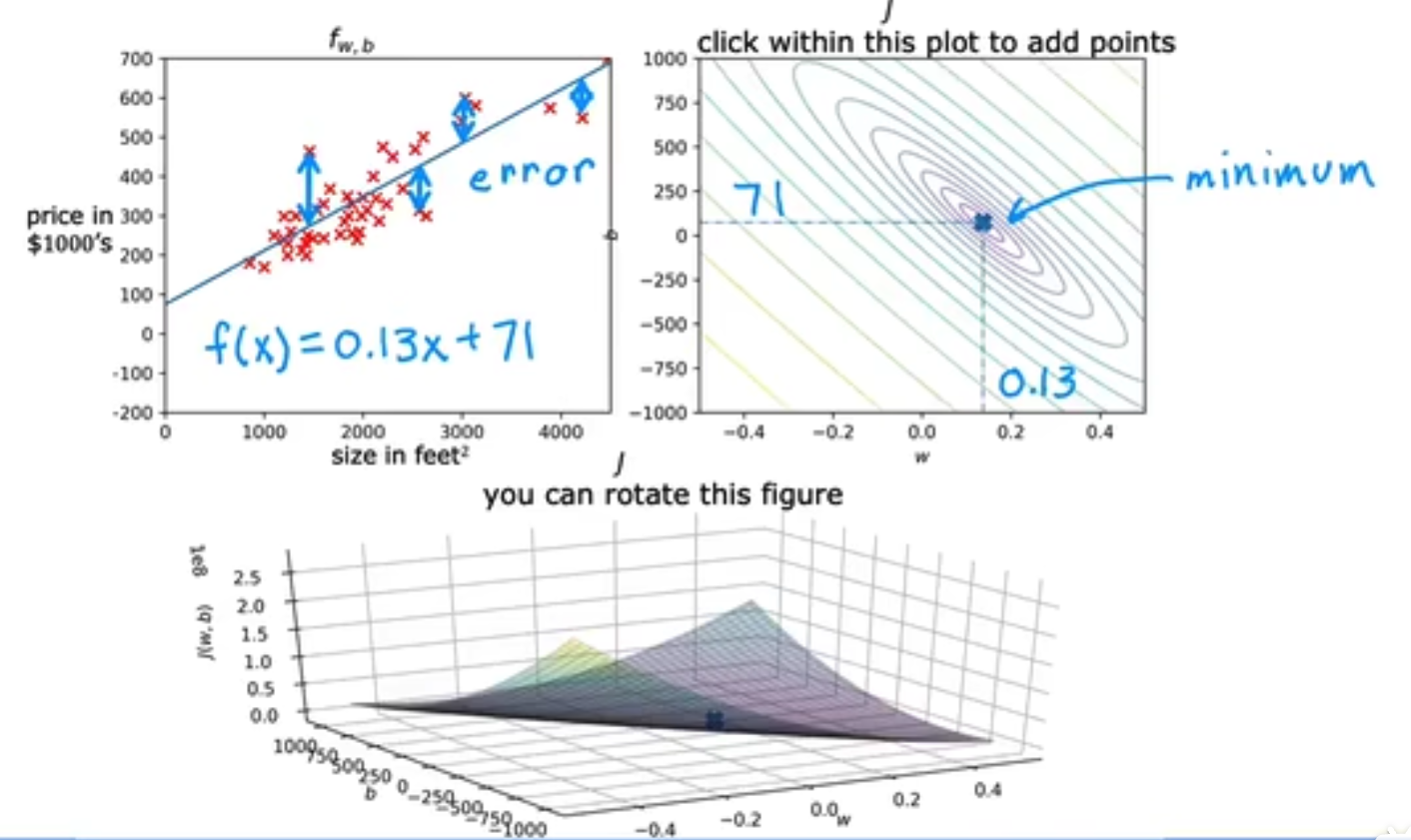
例如：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划中dp[j]是由dp[j-weight[i]]推导出来的，然后取max(dp[j], dp[j - weight[i]] + value[i])。

但如果是贪心，就是每次拿物品选一个最大的或者最小的就结束，和上一个状态没有关系。

所以贪心解决不了动态规划的问题。

总结就是，动规是由前一个状态推导出来的，而贪心是局部直接选最优的。

动规问题分类

基础问题

包括斐波那契数列、爬楼梯等动规基础问题

背包问题

是动规的经典系列，也是大厂面试很喜欢考察的类型。

打家劫舍

打家劫舍系列在力扣上一共三道题，最后一道是树形dp，也是比较经典的问题。

股票问题

类似今天买哪天卖可以获得最大利润，这个系列7-8题，也是较为经典的问题

子序列问题

子序列问题一般都是求最长递增子序列/最长连续递增子序列，以及非常经典的编辑问题（给两个字符串，问使得两个字符串相等的最小编辑数）

区间dp，概率dp主要是竞赛拔尖题目，过于难的动态规划一般面试不会考

DP注意点

看题解的时候不能过度注重递推公式，递推公式只是一部分，状态转移公式（递推公式）是很重要，但动规不仅仅只有递推公式。

解题步骤：五步

1. 状态转移的时候都会定义dp数组，需要知道dp数组的含义和下标的含义。例如求子序列问题，一般dp数组就是二维的，背包问题有时候也是二维的，此时我们就需要知道i和j分别是什么意思。

​ 同理，一维dp数组里面的数值和下标分别的含义，也都要搞清楚。

2. 递推公式：递推公式很重要，但是并不是动态规划所有的部分。

3. DP数组如何初始化：这一点需要首先想清楚DP数组下标和数值的含义。有的时候数组初始化成0，但是有的时候需要初始化成1，有的是i=1/i=2往后初始成0，往前初始成1。这些情况都有可能。

   （例如力扣题目：不同路径，在初始化的地方有坑，初始化是需要注意的）一些情况是递推公式决定了dp数组要如何初始化

4. DP数组遍历顺序：背包类的题目对遍历顺序很有讲究，例如01背包里面两个for循环，应该先遍历物品还是先遍历背包？遍历顺序从前到后/从后到前？

   完全背包问题，求排列和求组合，遍历顺序是完全不同的。

   背包问题的遍历顺序含义如下图所示：

在背包问题里，递推公式的类型其实很固定，关键就在遍历顺序上。大厂的算法题考察很可能是先给一道比较简单的题目，再一点一点变化，难度就会递增。背包问题可能出的变化就会在遍历顺序上，到时候可以进行一些衍生问题的整理。

5. 打印DP数组：DP类题目出问题很难直接通过代码看出来，需要直接打印DP数组，根据DP数组的含义和下标含义，看看逻辑是不是对的上。如果题目一直通过不了，打印出来的DP数组一定是有问题的，根据打印结果倒推递推公式和遍历顺序的问题。

debug考虑方向

• 题目举例推导状态转移公式？
• 打印dp数组的日志？
• 打印出来了dp数组和自己想的是否一样？

状态转移和遍历顺序/数组数值及下标含义都很重要。