📚 从递归阶乘到深度优先搜索

在学习深度优先搜索之前，我们先回顾一下递归阶乘的实现。递归阶乘是一种典型的递归算法，它通过将问题分解为更小的子问题来解决。

#include <iostream>
using namespace std;

int factorial(int n) {
    if (n <= 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

int main() {
    int n = 5;
    cout << n << "的阶乘为：" << factorial(n) << endl;
    return 0;
}

这样对于factorial(5),它的求解路线为

递归求解5的阶乘是以factorial(5)为起点，然后按照特定路线一路执行到终点factorial(1)结束的，这中间还经历了factorial(4),factorial(3),factorial(2)几个中间状态。

上述代码通过递归调用factorial函数来计算阶乘，我们可以将其视为一种深度优先搜索的实现方式。在每一次递归调用中，我们都深入到更小的子问题中，直到达到终止条件，然后回溯返回结果。

深度优先搜索是也从某个起点出发，经过若干个中间状态达到某个可能的终点状态。

但它还是带着搜索任务的算法，即在抵达终点前的每个状态上都可能面临着若干个选择，并且每次不同的选择往往还会影响到后面的选择结果，包括探索失败。

例如，假设你身处一座迷宫塔之中，每层塔都有固定的若干个通往下一层的入口，当选择其中一个入口下去时有可能成功进入到下一层大厅，也有可能发现是个死胡同，只能返回到上一层重新选择入口。

令f(n)表示当前身处塔的第n层，则从5楼开始探索下楼的路线时：从f(5)到f(4),从f(4)到f(3)，从f(3)到f(2)…都面临着若干种入口选择。

运气好我们既有可能一次性完成f(5)->f(4)->f(3)->f(2)->f(1),也有可能f(5)->f(4)->f(3)（此路不通）->f(4)(回到4楼重新选择)->…

深度优先搜索(DFS)模式，其基本思想是:

先选择某一种可能的情况向前搜索，直到无路可走，再退回到上一个状态，探寻其它的方向可能。

如此循环往复，直到得到题解或证明无解。

这一过程也可称之搜索与回溯。

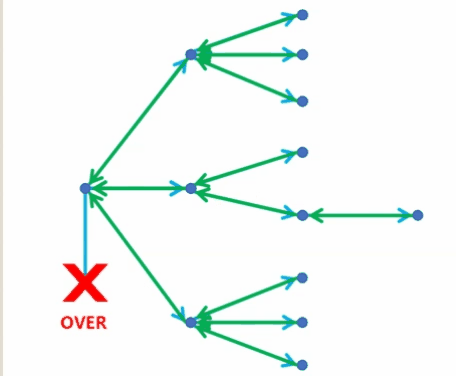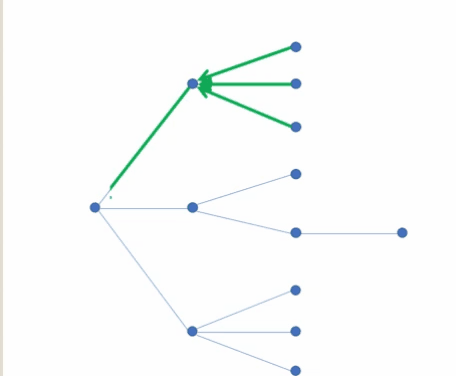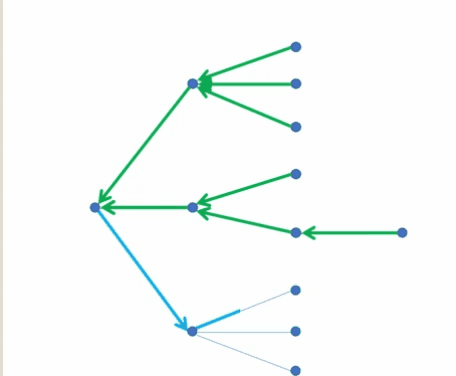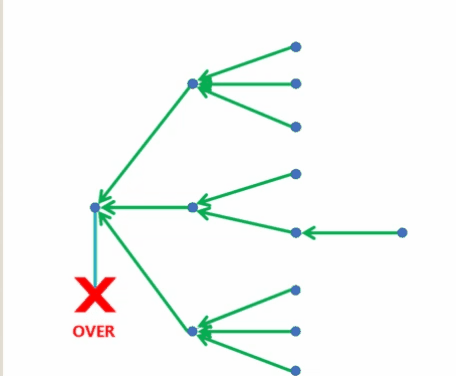
两个动图更好地理解深度优先搜索（搜索与回溯）

🗝️ 密码锁的所有密码组合

现在，我们来解决一个实际问题：列举一个3位密码锁的所有可能的密码组合。密码锁的每一位数字可以选择0~9之间的任意一个数字。

💡 思路解析:

• 定义一个长度为3的数组digits，用于存储密码锁的每一位数字。
• 使用一个递归函数dfs来遍历密码锁的所有可能的密码组合。
• 在递归函数中，通过循环遍历0~9之间的数字，依次将每个数字赋值给当前位的密码。
• 如果遍历到了最后一位密码，即第3位，将当前的密码组合输出。
• 否则，递归调用dfs函数，深入到下一位密码的选择中。

#include <iostream>
using namespace std;

void dfs(int depth, int digits[]) {
    if (depth == 3) {
        cout << digits[0] << digits[1] << digits[2] << endl;
        return;
    }
    for (int i = 0; i <= 9; i++) {
        digits[depth] = i;
        dfs(depth + 1, digits);
    }
}

int main() {
    int digits[3] = {0};
    dfs(0, digits);
    return 0;
}

通过以上代码，我们可以得到密码锁的所有可能的密码组合。这个例子展示了深度优先搜索的一种典型应用方式，通过递归和回溯来遍历问题的所有可能解。

🔄 全排列问题

全排列是另一个常见的深度优先搜索问题。给定一个不重复的数字序列，求出其所有可能的全排列。

💡 思路解析:

• 使用一个递归函数dfs来遍历全排列。
• 在递归函数中，通过循环遍历未被选中的数字，将当前数字加入到排列中，并将该数字标记为已选中。
• 如果排列中的数字个数达到了序列的长度，将该排列输出。
• 否则，递归调用dfs函数，深入到下一个数字的选择中。
• 在回溯到上一个状态时，需要将当前数字从排列中移除，并将其标记为未选中，以便进行下一次选择。

#include <iostream>
#include <vector>
using namespace std;

void dfs(vector<int>& nums, vector<int>& path, vector<bool>& used, vector<vector<int>>& res) {
    if (path.size() == nums.size()) {
        res.push_back(path);
        return;
    }
    for (int i = 0; i < nums.size(); i++) {
        if (used[i]) {
            continue;
        }
        path.push_back(nums[i]);
        used[i] = true;
        dfs(nums, path, used, res);
        path.pop_back();
        used[i] = false;
    }
}

vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> used(nums.size(), false);
    dfs(nums, path, used, res);
    return res;
}

int main() {
    vector<int> nums = {1, 2, 3};
    vector<vector<int>> permutations = permute(nums);
    for (const vector<int>& permutation : permutations) {
        for (int num : permutation) {
            cout << num << " ";
        }
        cout << endl;
    }
    return 0;
}

通过以上代码，我们可以得到数字序列的所有全排列。这个例子展示了

深度优先搜索在解决全排列问题时的应用。通过递归和回溯，我们可以遍历所有可能的排列情况。

🔢 素数环问题

素数环是指一组素数按照环状排列的情况，其中每两个相邻的素数的和也是素数。给定一个正整数n，求解n个数字的素数环。

💡 思路解析:

• 定义一个长度为n的数组nums，用于存储素数环的数字。
• 使用一个递归函数dfs来遍历素数环。
• 在递归函数中，通过循环遍历1~n之间的数字，依次将每个数字赋值给当前位置。
• 如果当前位置的数字与之前的数字构成素数，则继续递归深入。
• 如果遍历到了最后一位数字，即构成了一个素数环，则输出该素数环。
• 否则，递归调用dfs函数，深入到下一个位置的数字选择中。

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

bool isPrime(int num) {
    if (num <= 1) {
        return false;
    }
    for (int i = 2; i <= sqrt(num); i++) {
        if (num % i == 0) {
            return false;
        }
    }
    return true;
}

void dfs(int depth, int n, vector<int>& nums, vector<bool>& visited) {
    if (depth == n) {
        if (isPrime(nums[0] + nums[n - 1])) {
            for (int num : nums) {
                cout << num << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = 2; i <= n; i++) {
        if (!visited[i] && isPrime(nums[depth - 1] + i)) {
            nums[depth] = i;
            visited[i] = true;
            dfs(depth + 1, n, nums, visited);
            visited[i] = false;
        }
    }
}

void primeRing(int n) {
    vector<int> nums(n);
    vector<bool> visited(n + 1, false);
    nums[0] = 1;
    visited[1] = true;
    dfs(1, n, nums, visited);
}

int main() {
    int n = 4;
    primeRing(n);
    return 0;
}

通过以上代码，我们可以得到n个数字的素数环。在深度优先搜索过程中，我们通过判断相邻数字的和是否为素数来确定下一个数字的选择，从而构建出满足条件的素数环。

📚 总结

深度优先搜索是一种重要的算法思想，常用于解决图遍历、排列组合和搜索问题。通过递归和回溯的方式，我们可以遍历问题的所有可能解，并找到满足特定条件的解。通过以上的例子，我们掌握了深度优先搜索的基本原理和应用，希望能够在实际问题中灵活运用。

⭐️希望本篇文章对你有所帮助。

⭐️如果你有任何问题或疑惑，请随时向提问。

⭐️感谢阅读！