3 Linear Regression
Linear Regression即是根据数据做出预测,如下,
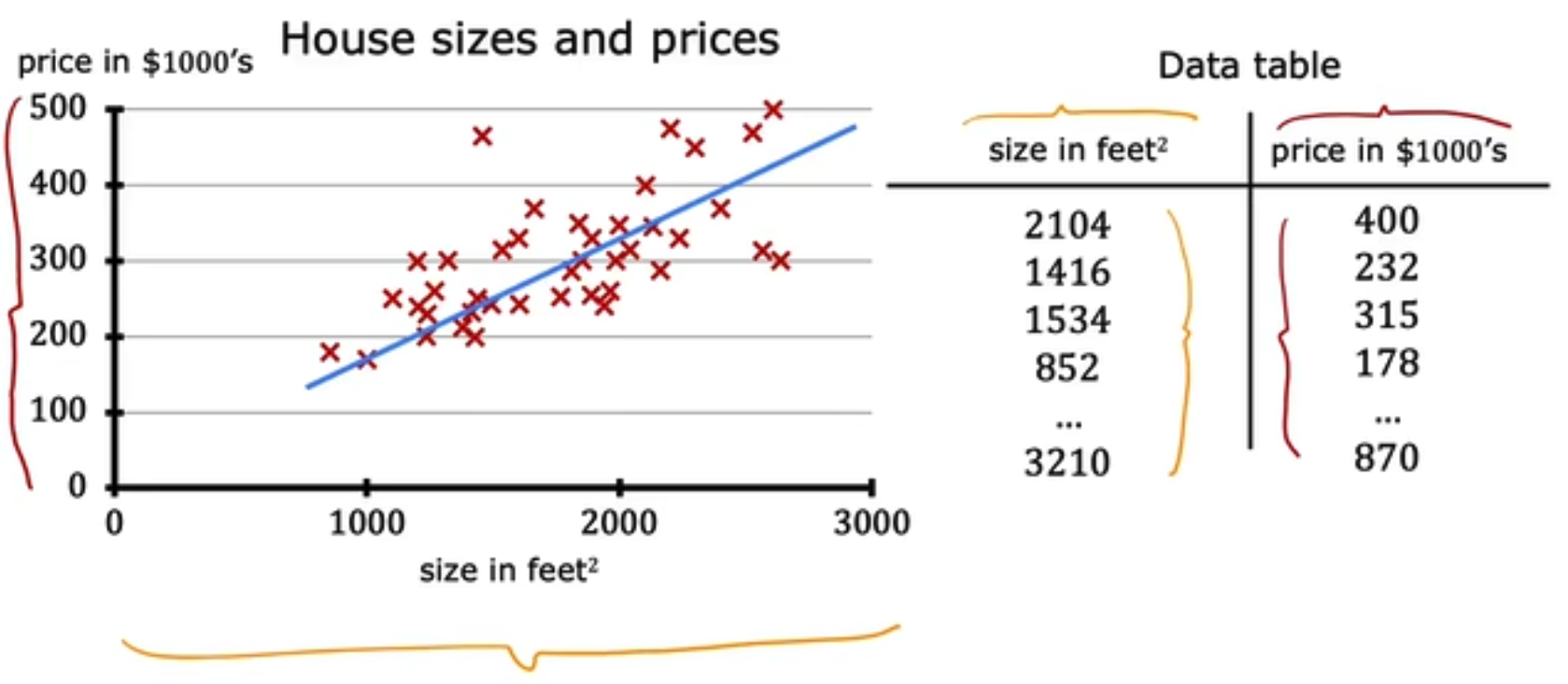
training set 如下:
在Linear Regression中你可以将(x, y)看做如下,每一行是一个sample,而每一列除最后一列是一个feature,最后一列是label。

我们使用training set来拟合我们的模型,例如LR中模型往往是y_hat = Wx + b,我们需要拟合的可学习参数是W和b,但是如何拟合这个W和b取决于你的数据,模型和你要使用的策略/cost func,以使用MSE为cost为例,J(w,b)式子中的1/2m中的2是为了方便计算,求导时抵消掉平方上的2,而m是为了方便求取均值,如下,

对cost func有更直观的理解,我们简化bias=0,如下,
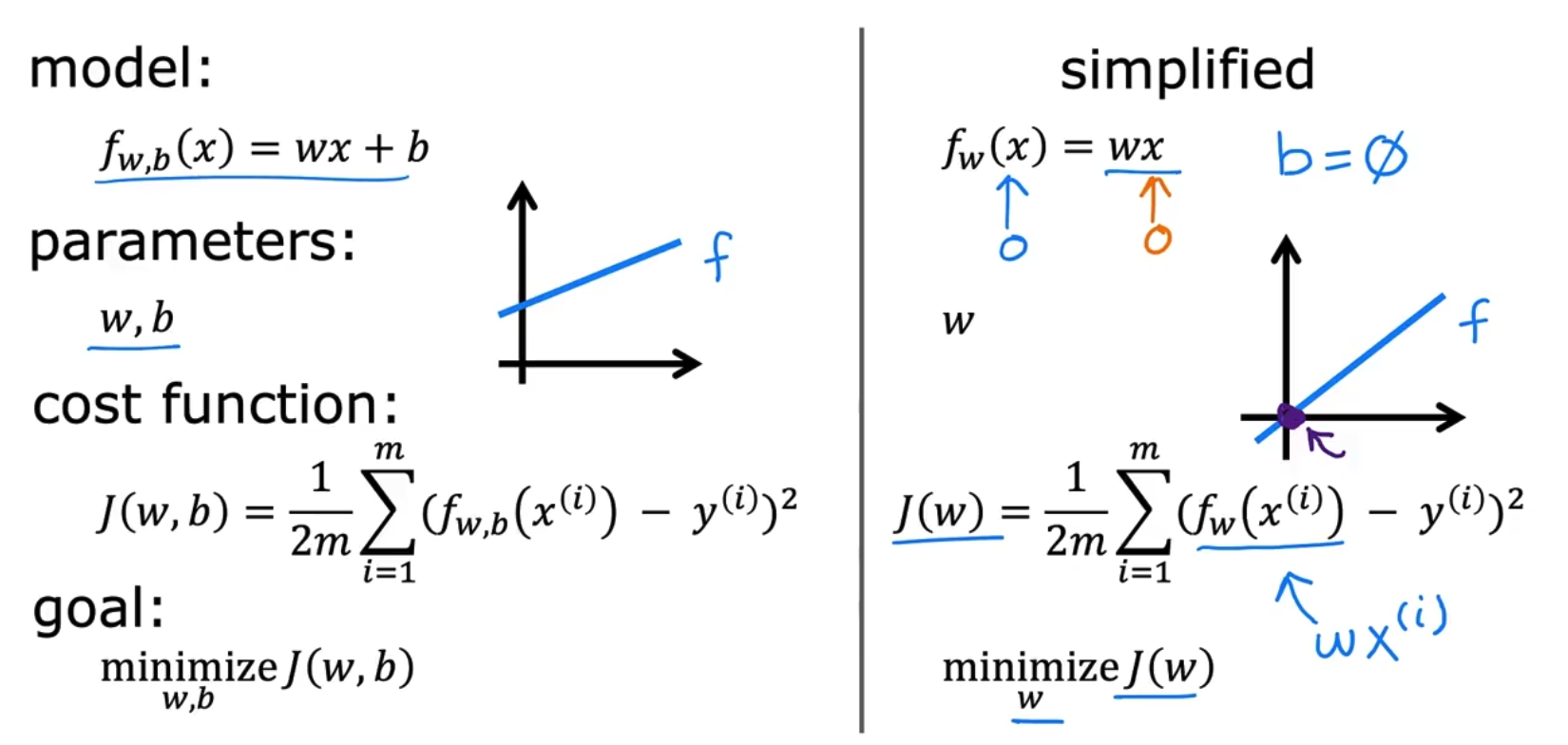
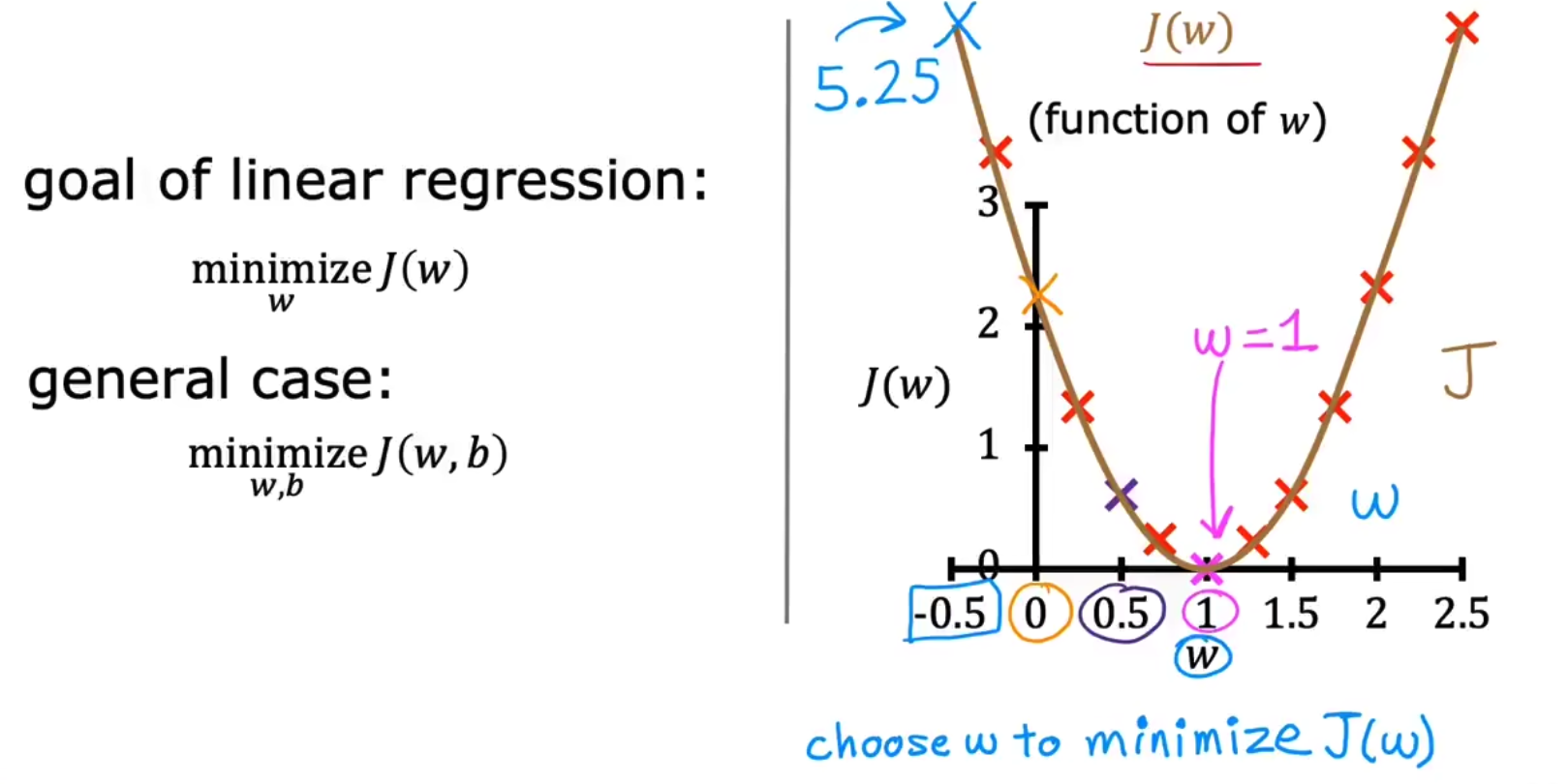
我们绘制J(w)-w曲线,并绘制当w取特定值时对应的f(x)-x曲线,如下为取w=1,即y=x曲线的结果:
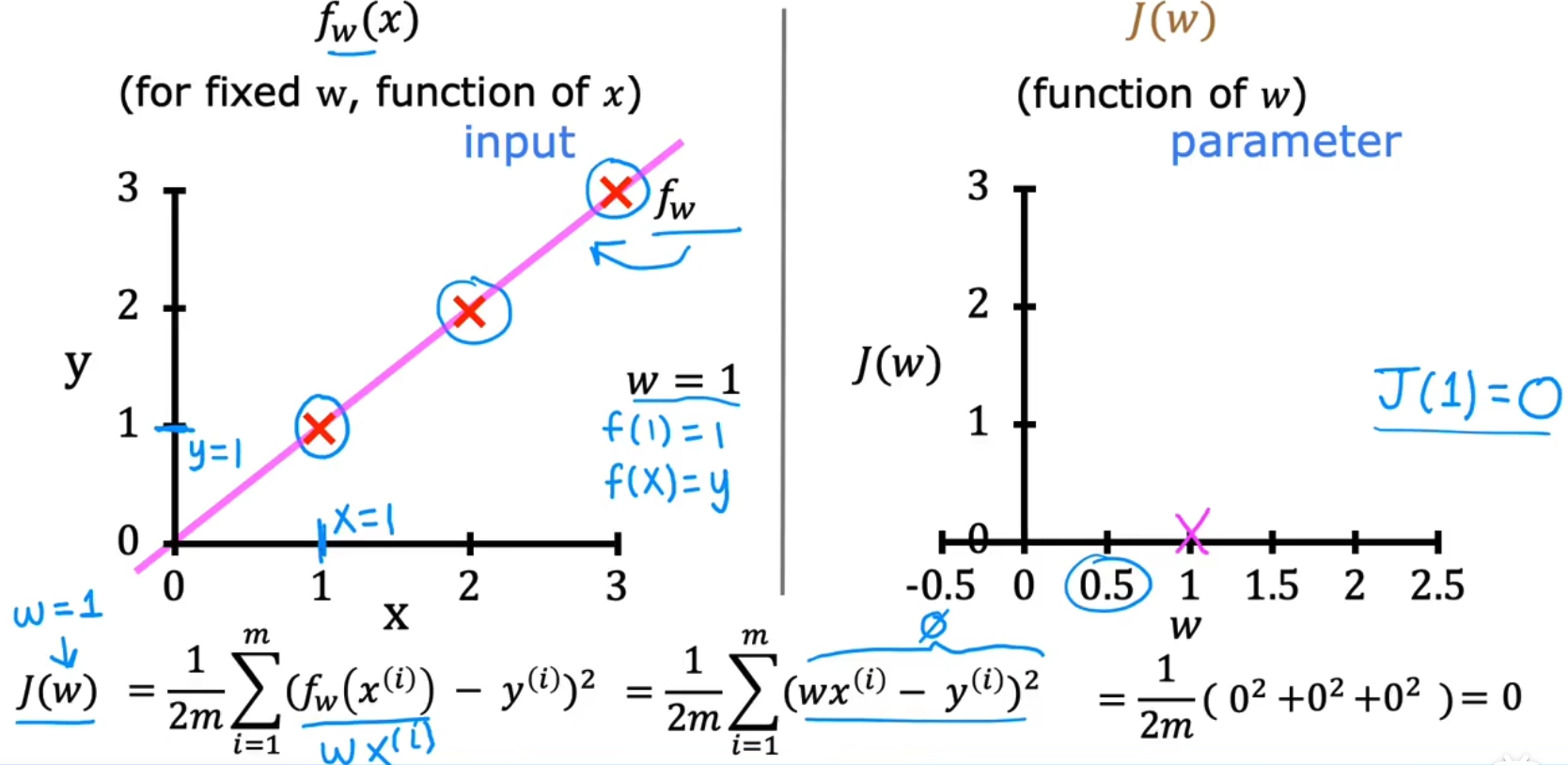
由于w是随机选取的,我们同样也可以选取w=0,y=0得到一组数据。我们使用枚举法生成所有w选取和对应J(w),最终绘制J(w)-w曲线如下,
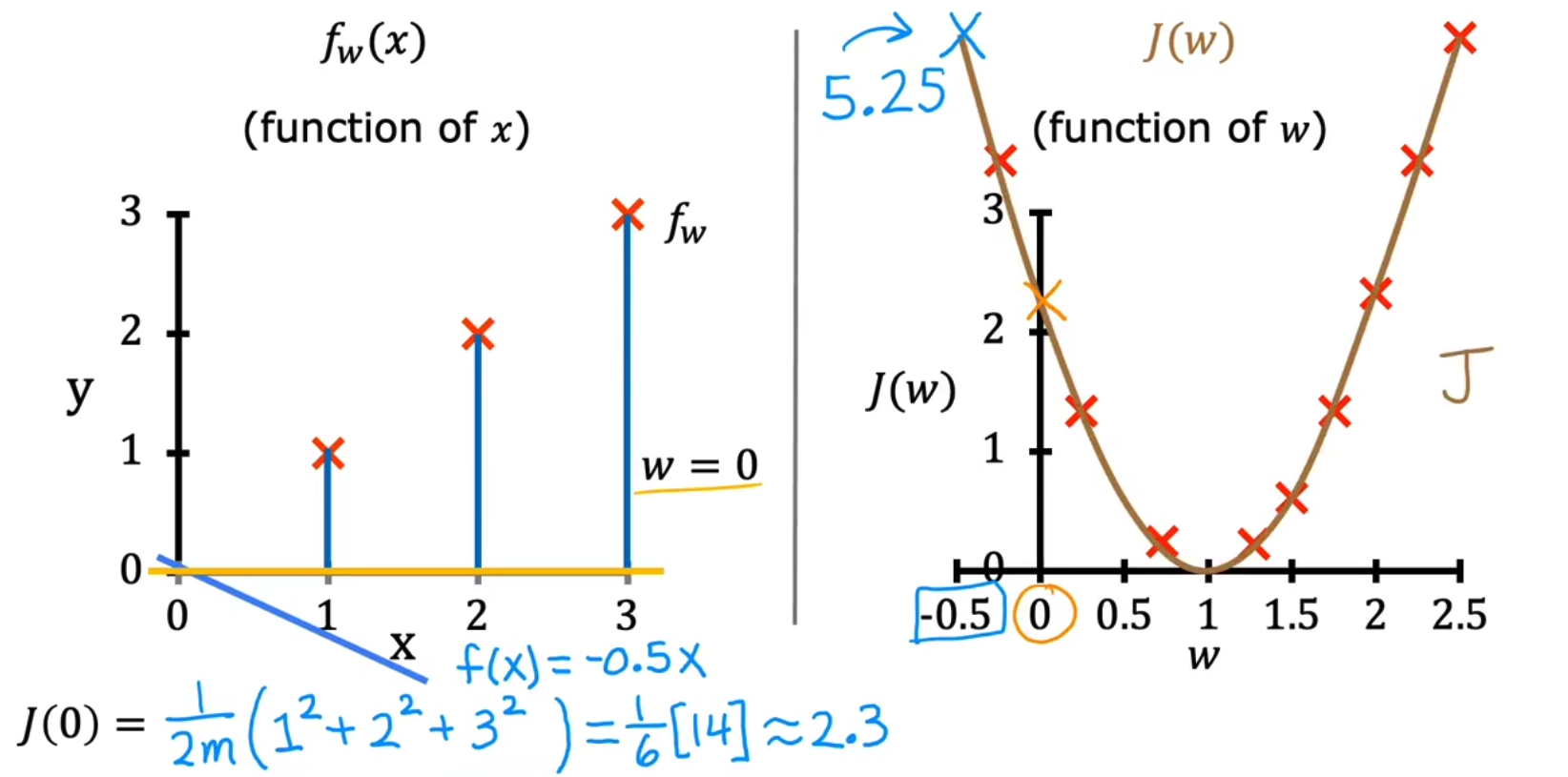
所以其实LR的最终目的是要argmin( J(W, b) )
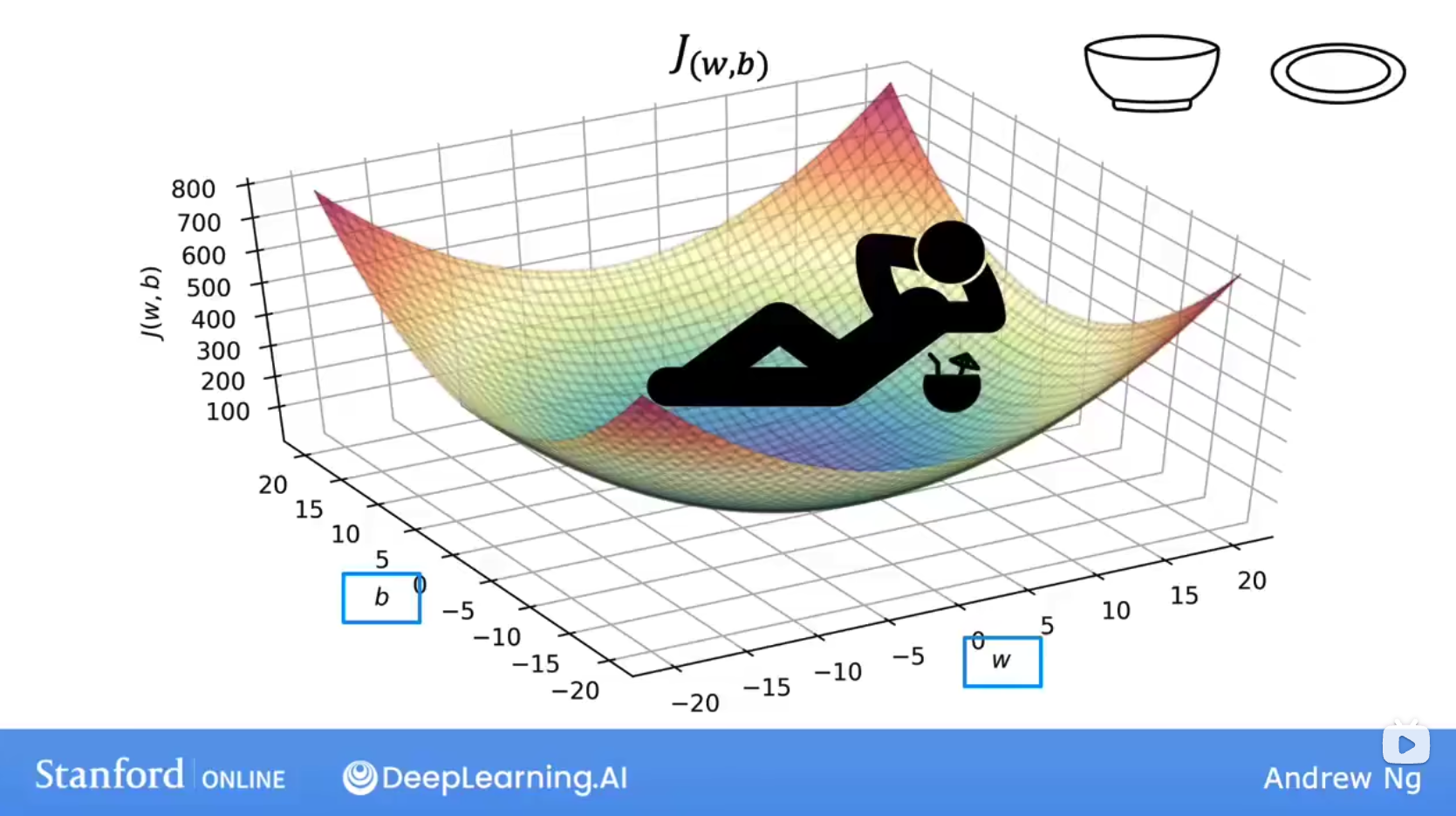
接下来,让我们更加直观的来了解cost func,当我们引入w, b双参时,它的cost func J(w, b)如下,这取决于你的数据集和执行的cost func,但其实dataset占据主导。
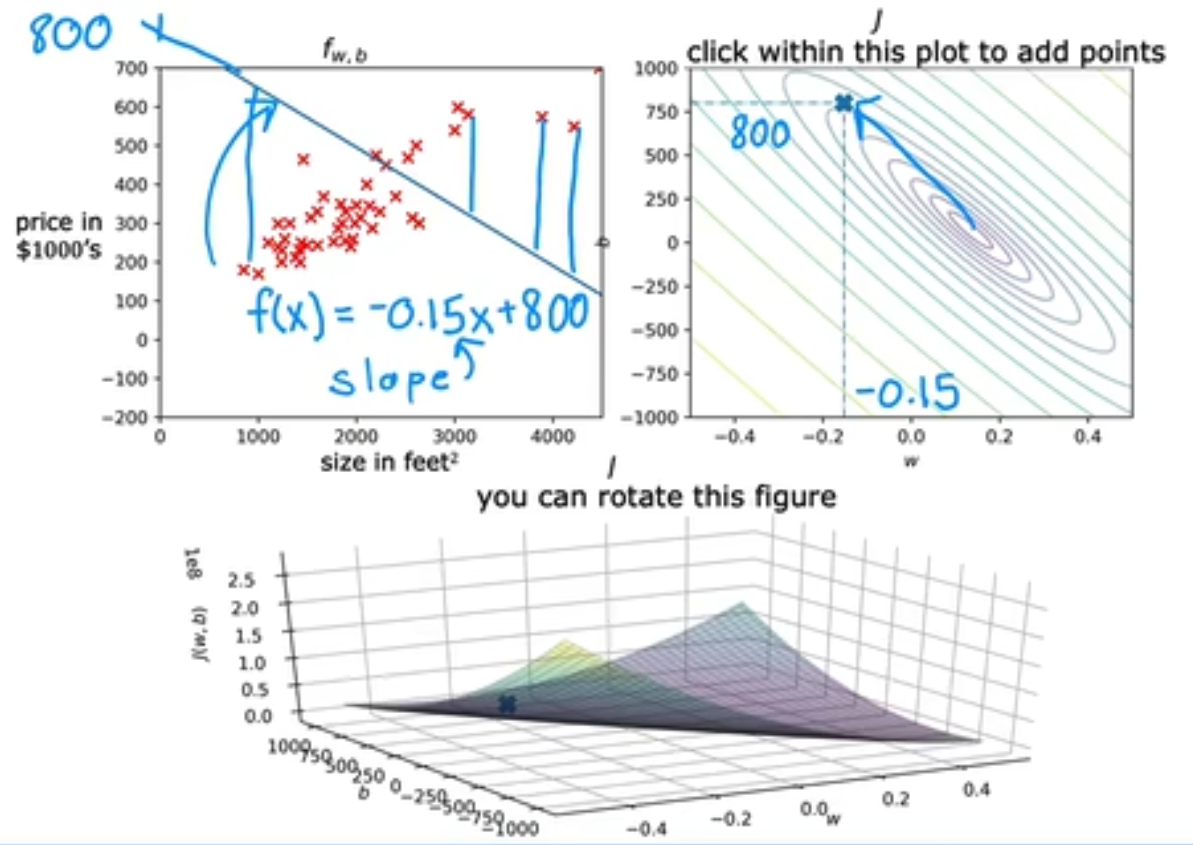
为了同时更新损失值J(w, b),weight,以及bias之间的关系,我们将使用等高线来可视化结果,例如当(w, b)的选取同(-0.15, 800)时,它离中心点相差很远,拟合效果不好。
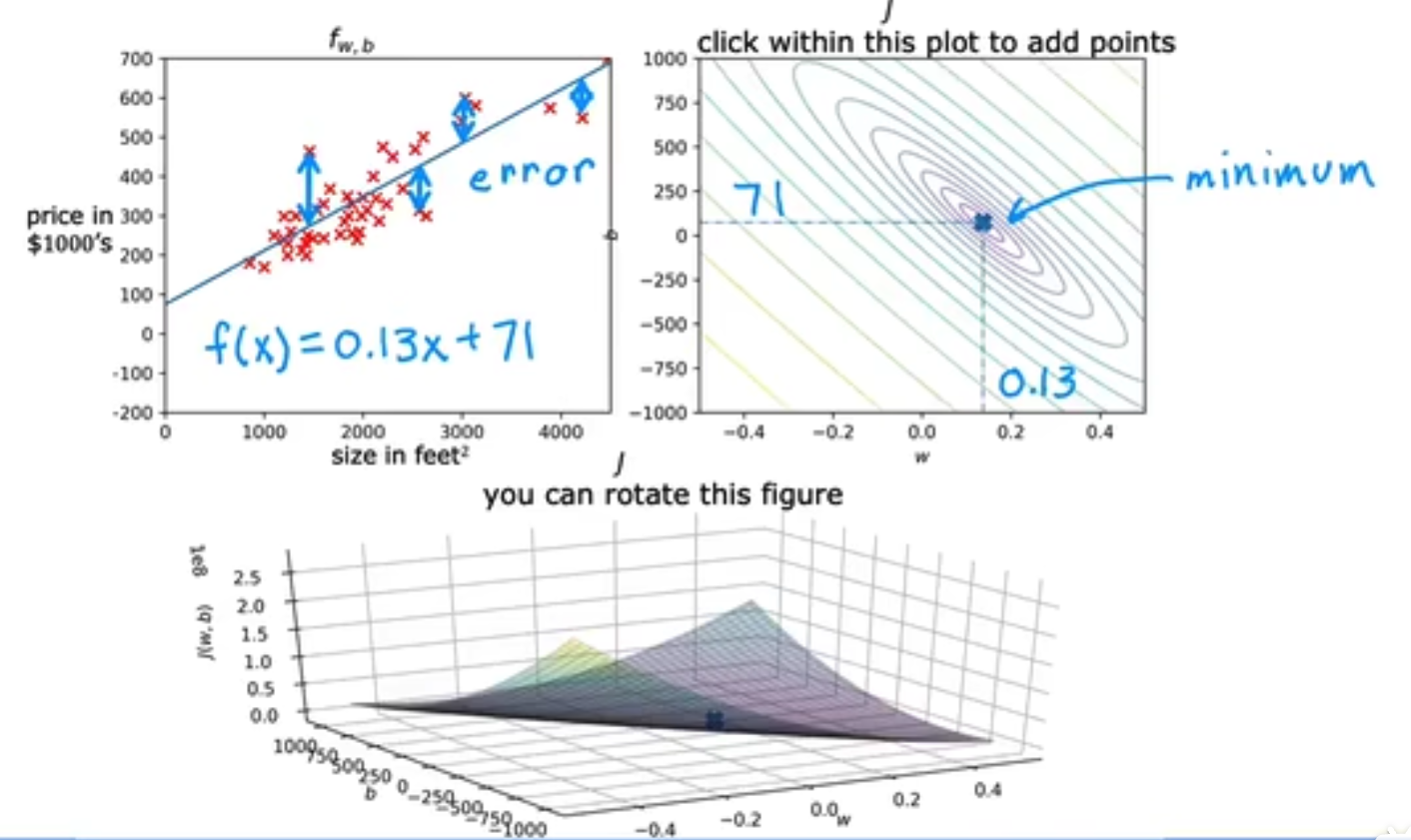
当(w, b)==(0, 360)时,

需要注意到的是,当在同一等高线时,即意味着损失函数的值相等,但其实就算相等也是不同的(w, b)值,这对我们的教训是**cost可能相等,但就算相等,也是对应了不同的w,b值 **








![[已解决]Springboot项目启动时端口被占用](https://img-blog.csdnimg.cn/c7e90a70dfff48fabd1871be5b602ac2.png)



