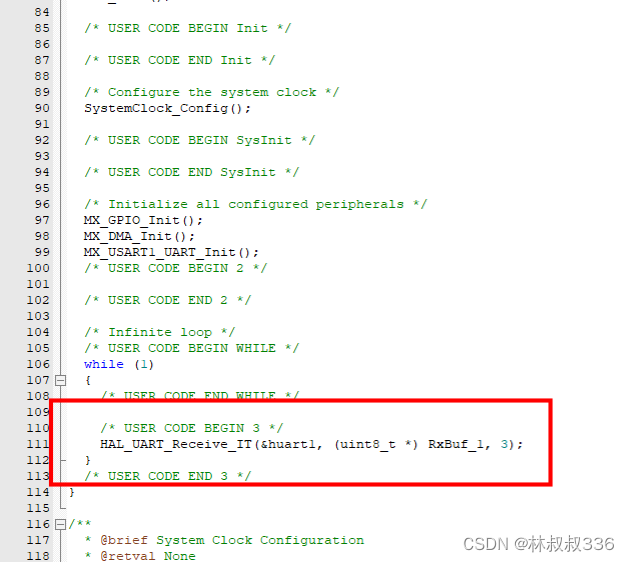
我们在上一个章节中学习了损失函数，我们的最终目的是要求得损失函数最小化的weight和bias，那么如何做到这一点呢，我们引入梯度下降算法，

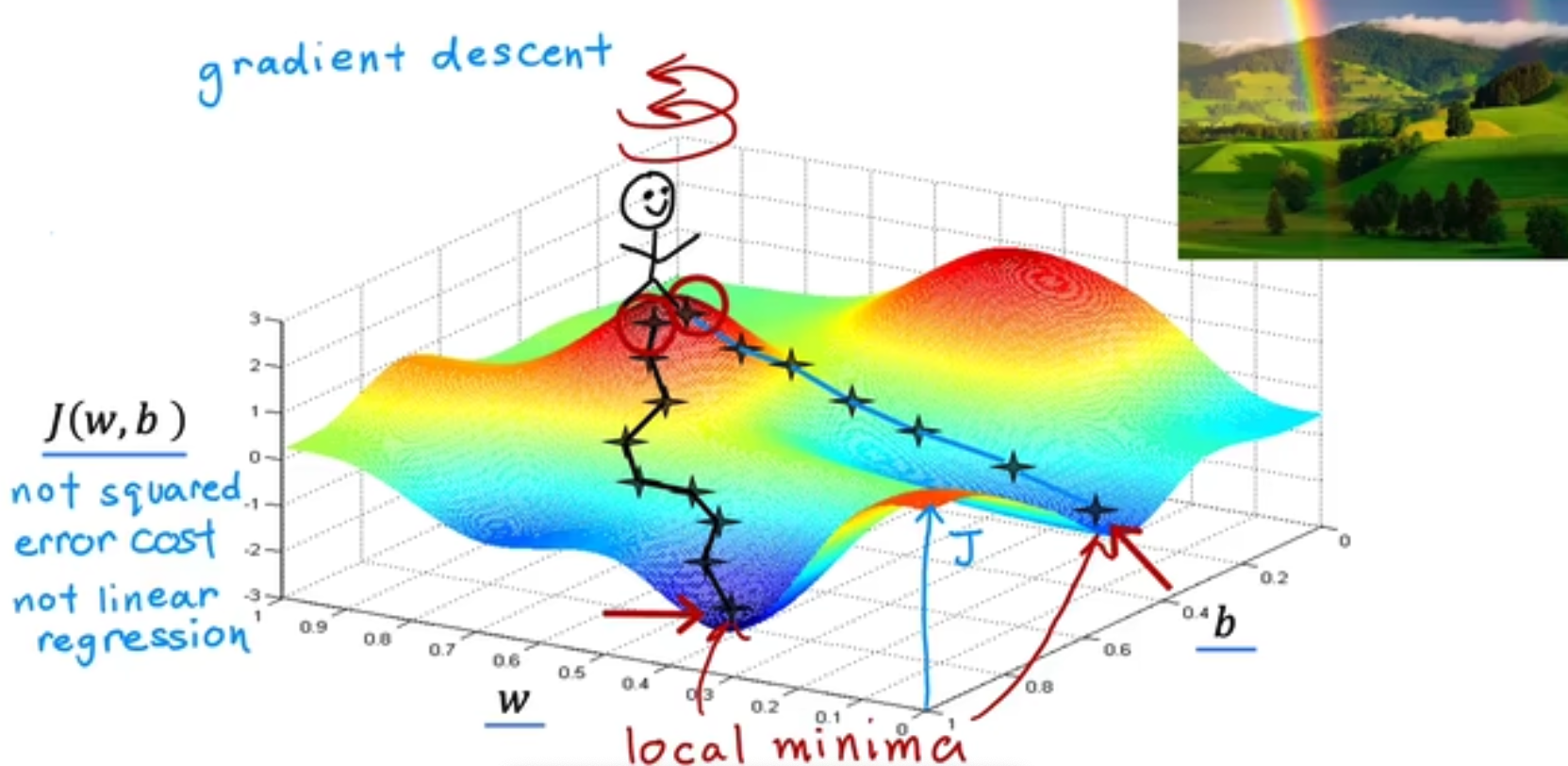
请注意，对于Linear Regression + MSE，你得到的J(w, b)和w, b的图必然是一个如大碗状的凸函数，而策略Gradient Descent只是决定你该如何下降到这个最低点。但是对于别的模型，你的损失函数图可能会存在多个局部最优点，你会去往哪个最低点，这往往取决于你的起始点（权重初始化）和baby-step大小（learning rate），如下，

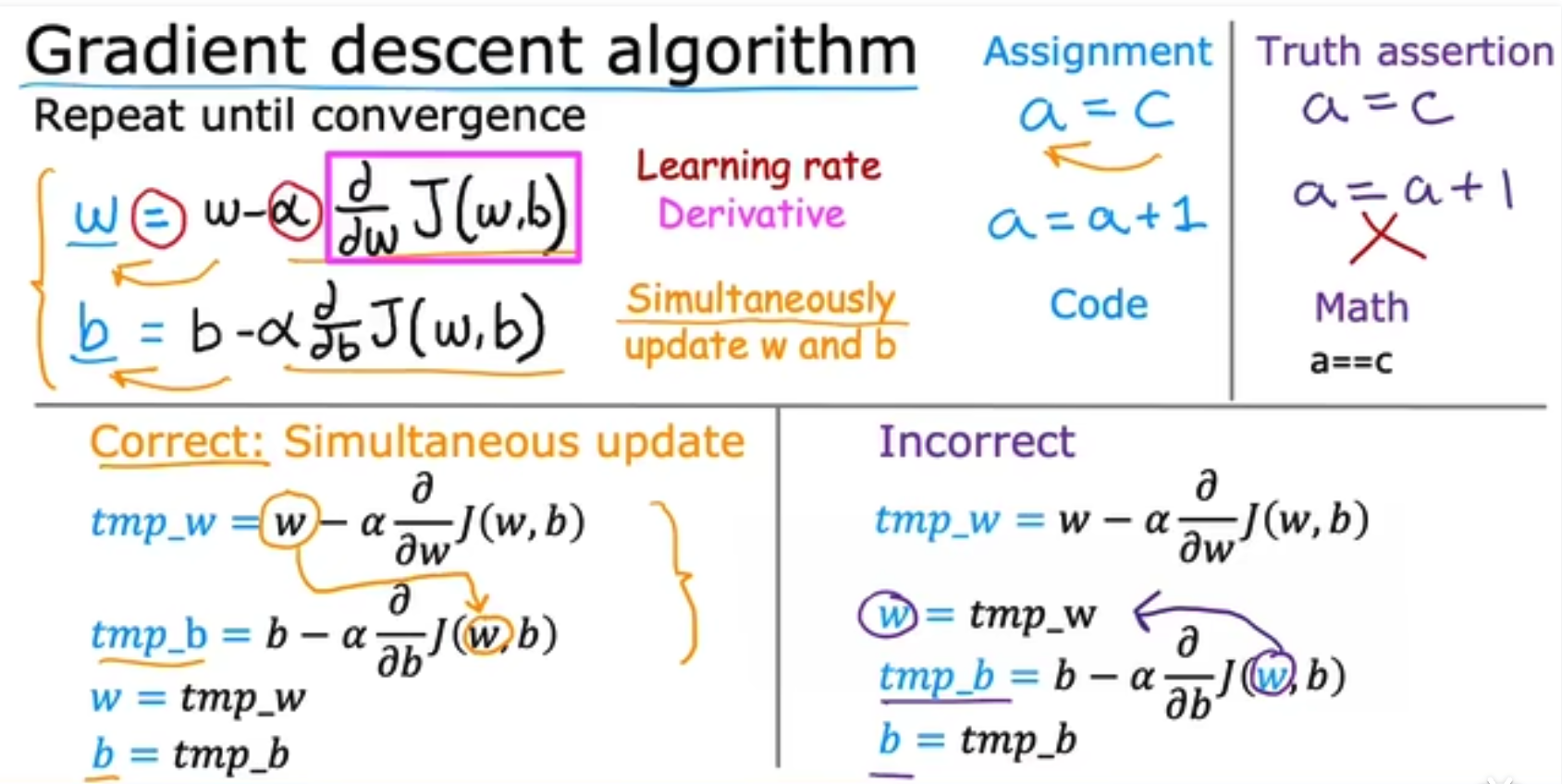
我们将上面的下降过程通过数学表达式的方式来呈现，我们的结果如下，偏微分部分决定了下降方向，alpha决定了步子的大小。需要注意到是，我们的W和b是同步更新的，即在计算b时我们使用的是未更新的W。

为了对GD中的偏导数有一个更直观的理解，我们同样将bias=0，然后观察weight在GD中的变化，我们发现初始点不论是在最低点的左侧或者右侧，GD算法都很好地做到了他应该做的事情：将J(W)下降到最小。

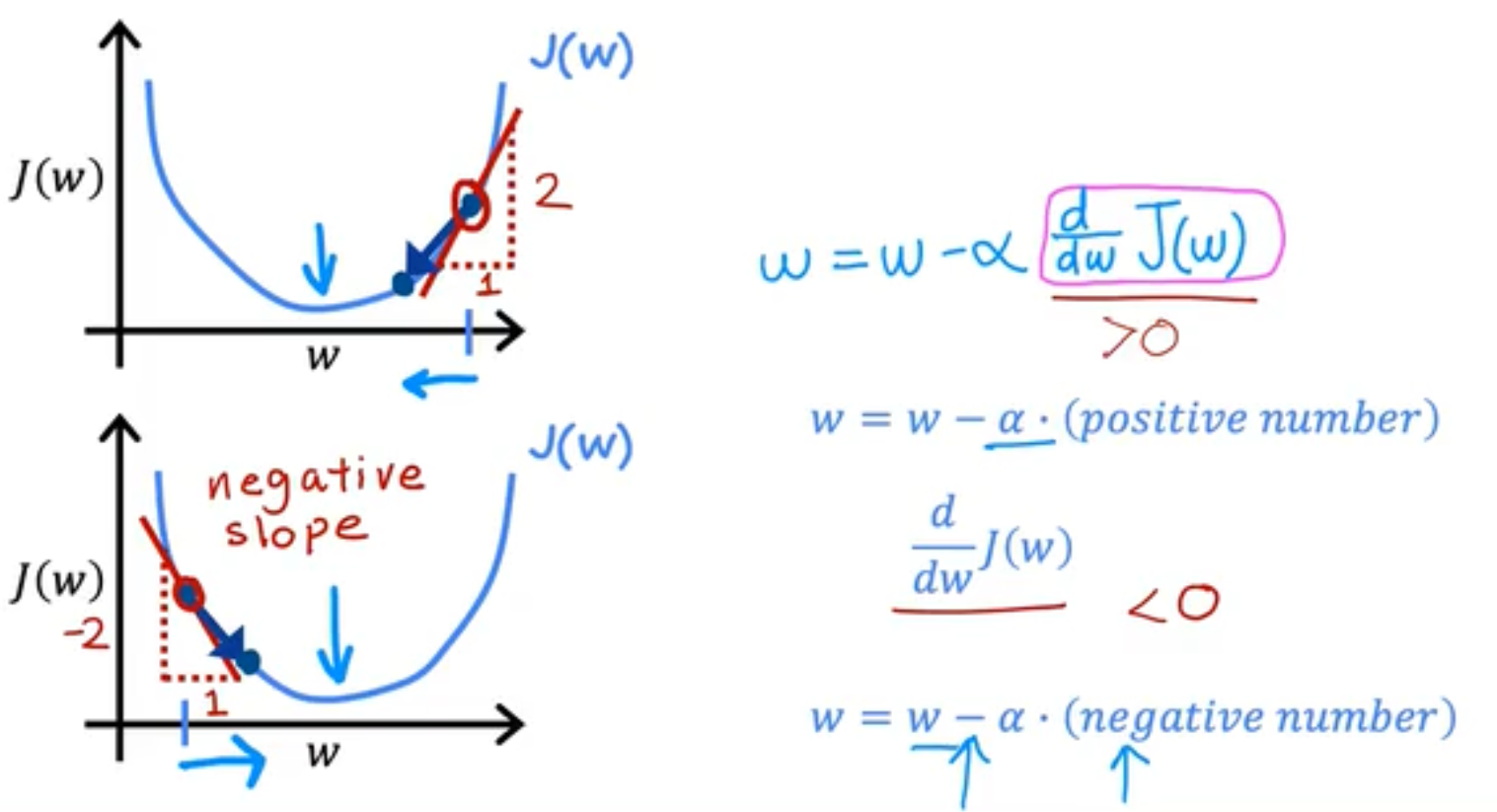
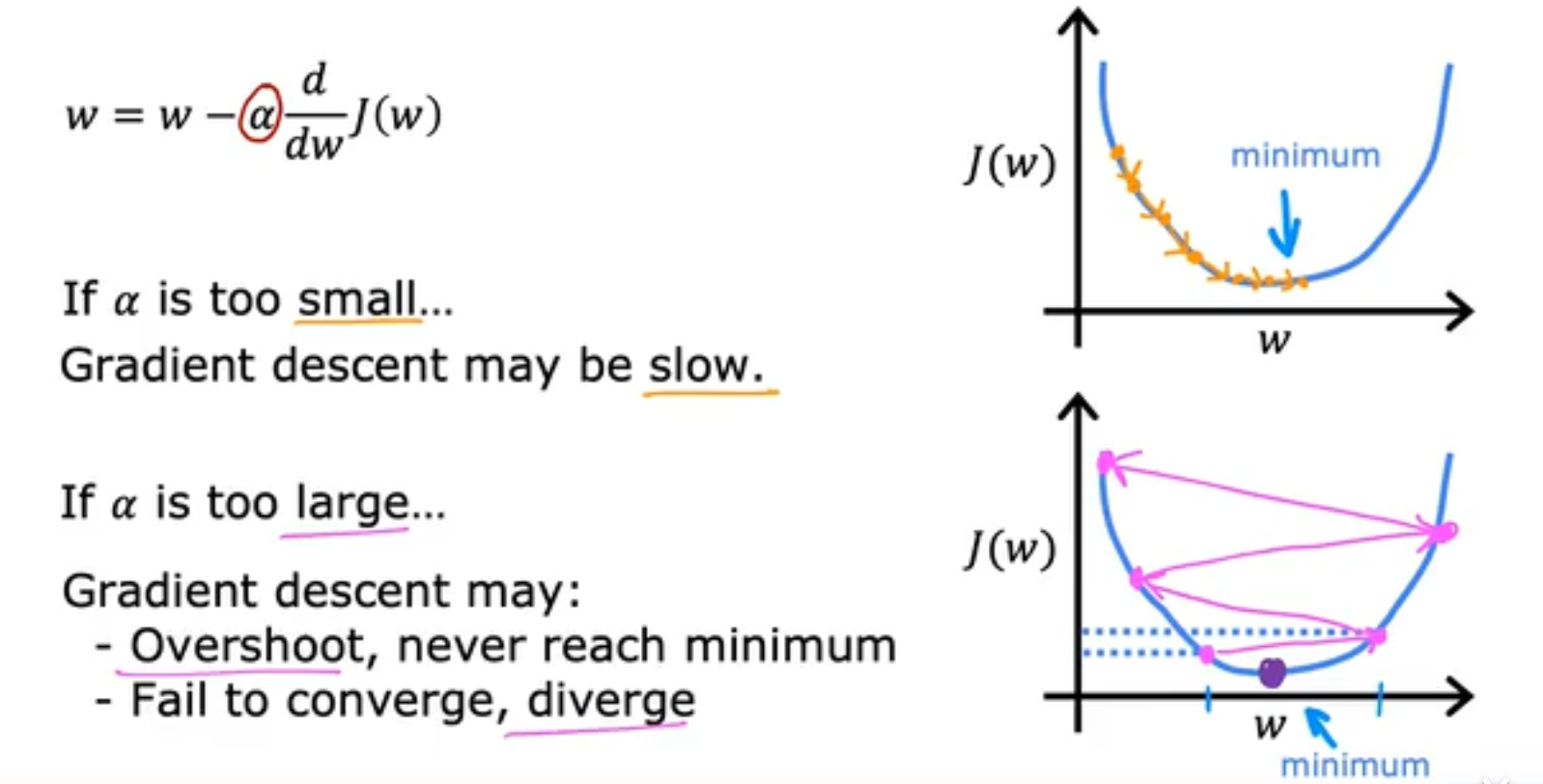
接下来我们将重点探讨一下Learning Rate学习率带来的变化。如果Learing rate选取的太小，那么收敛地会很慢；如果Learning rate选取的太大，那么可能会fail to converge无法收敛，

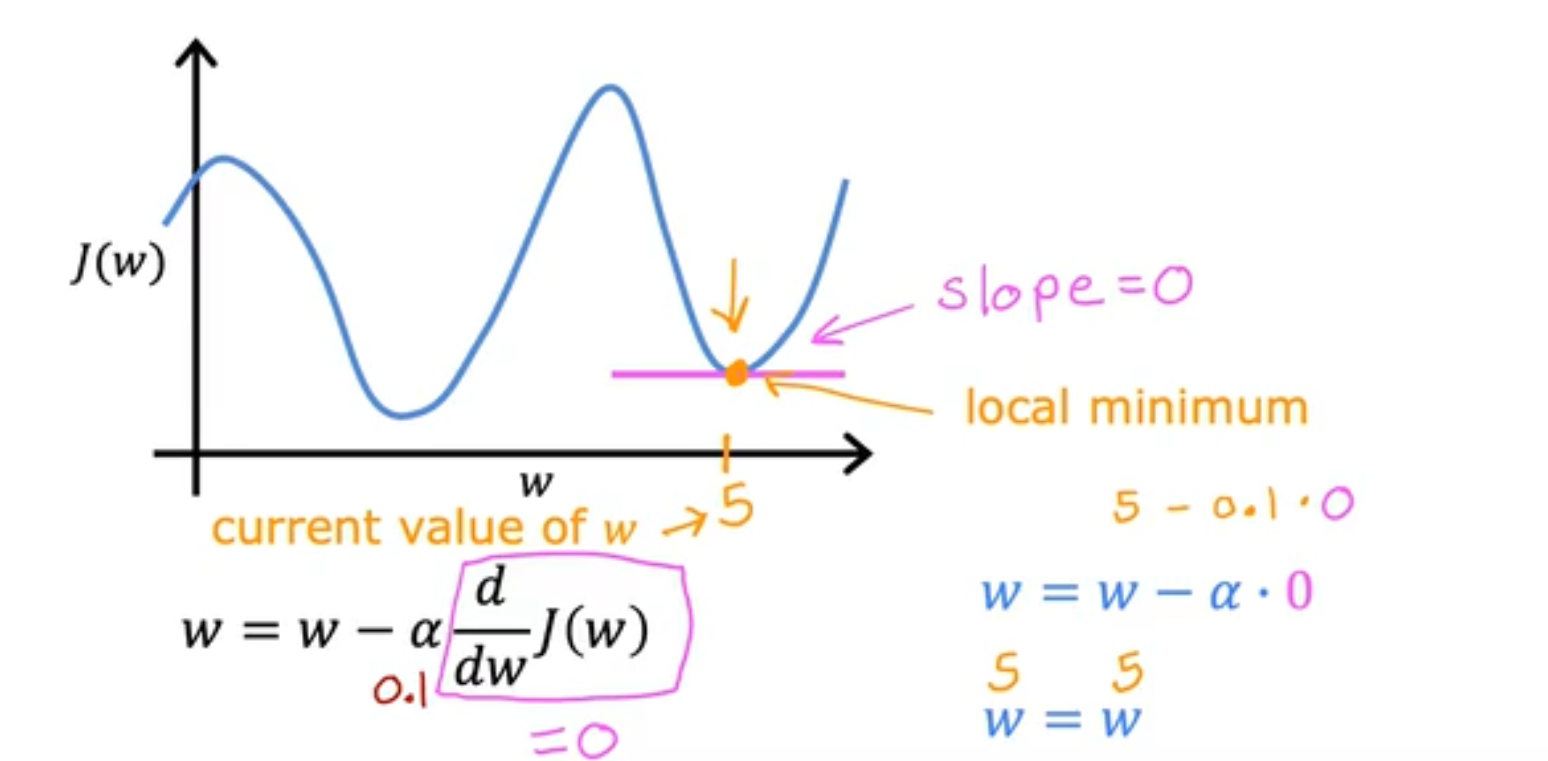
而局部最优解的存在更是破坏性的，这会使得你的导数在局部最优解时无法进行移动，始终保持在局部最优解。

接下来我们将会把上面学习到的知识全部结合起来，即我们使用Linear R的model，使用MSE的策略，使用Grandient D的算法。

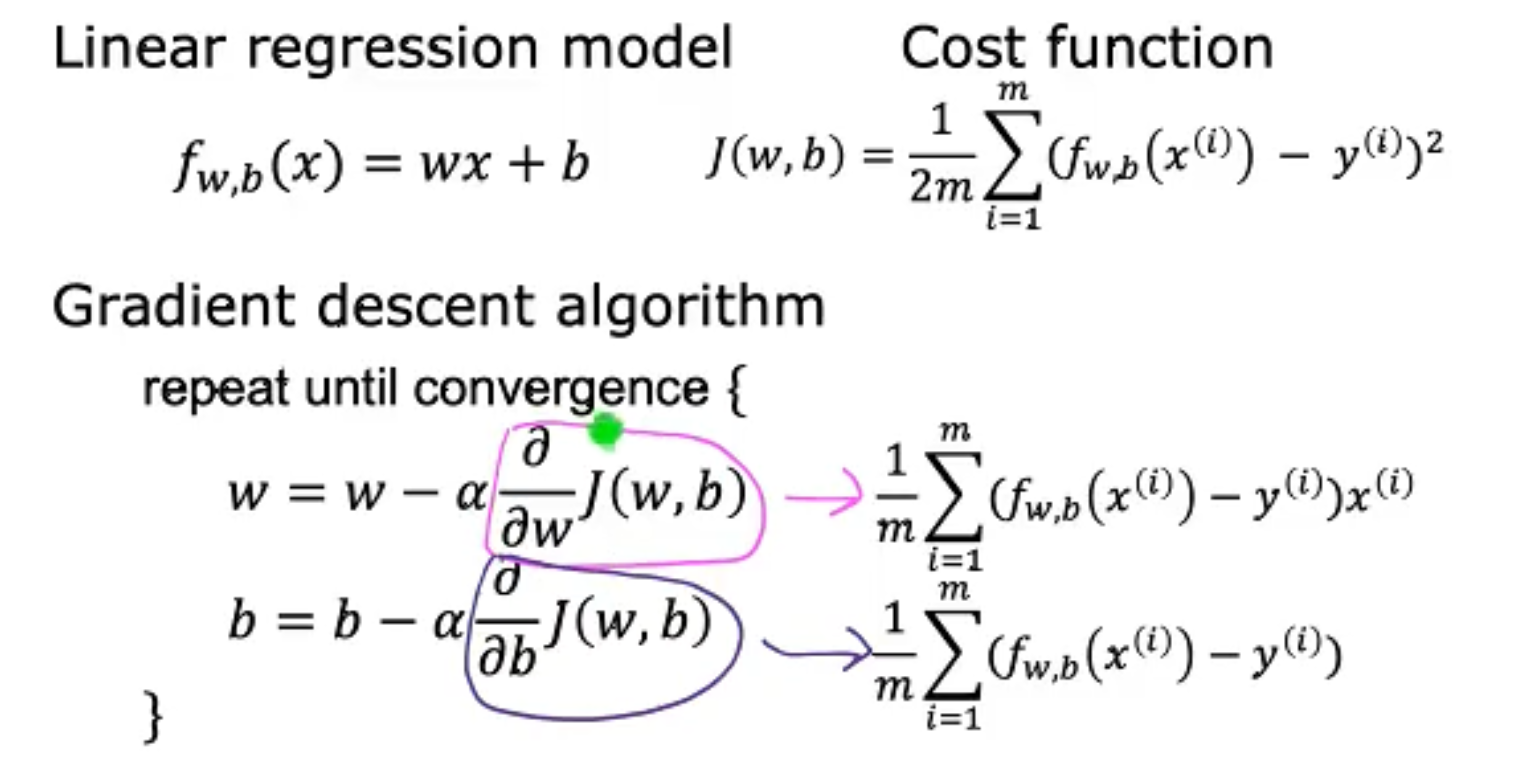
在Gradient D中我们需要求取偏导，对于w和b的偏微分的求取过程如下，

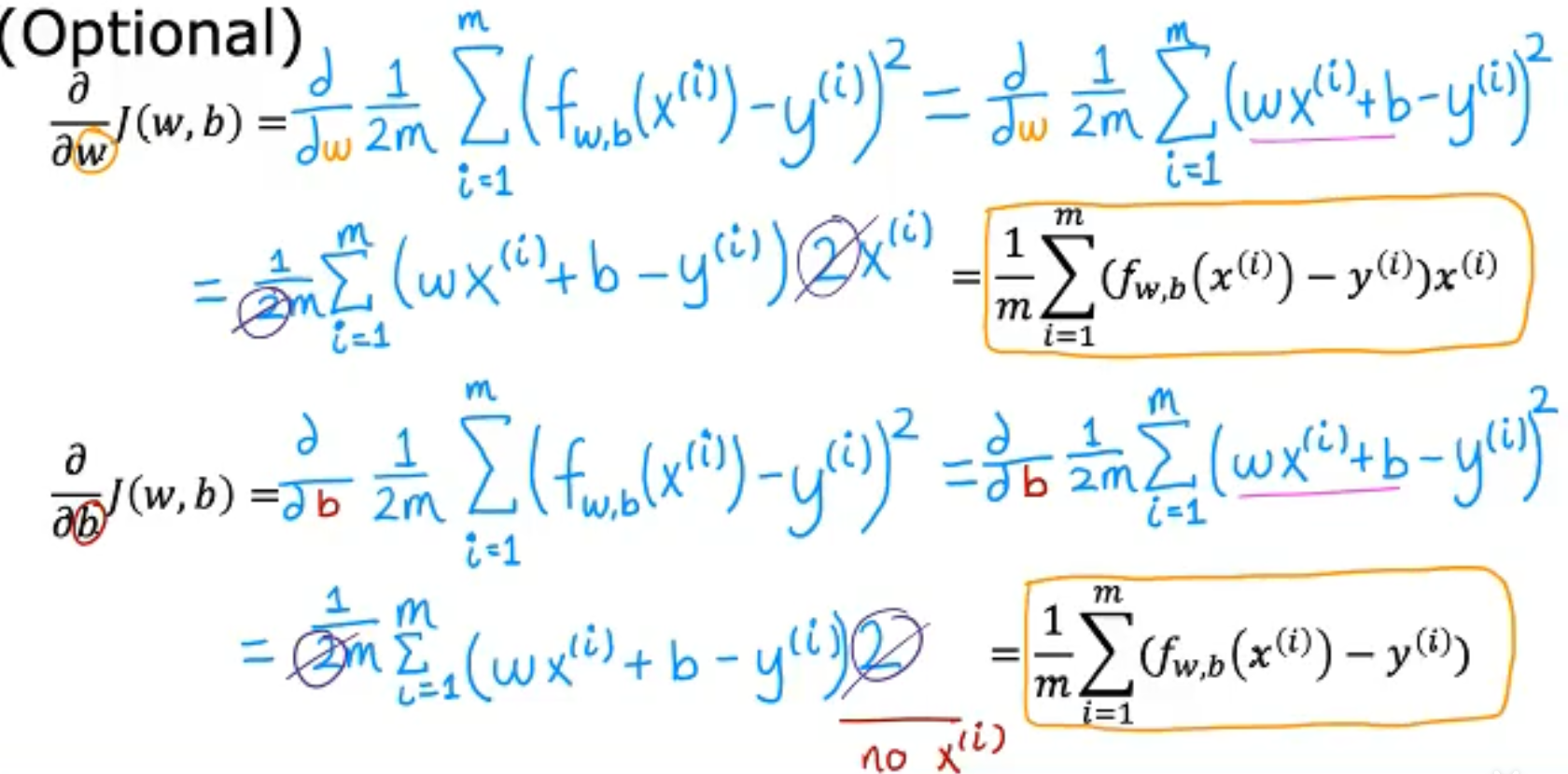
当我们采用Linear R作为模型，而使用MSE作为策略时，我们的J函数永远都是Convex func，如下，

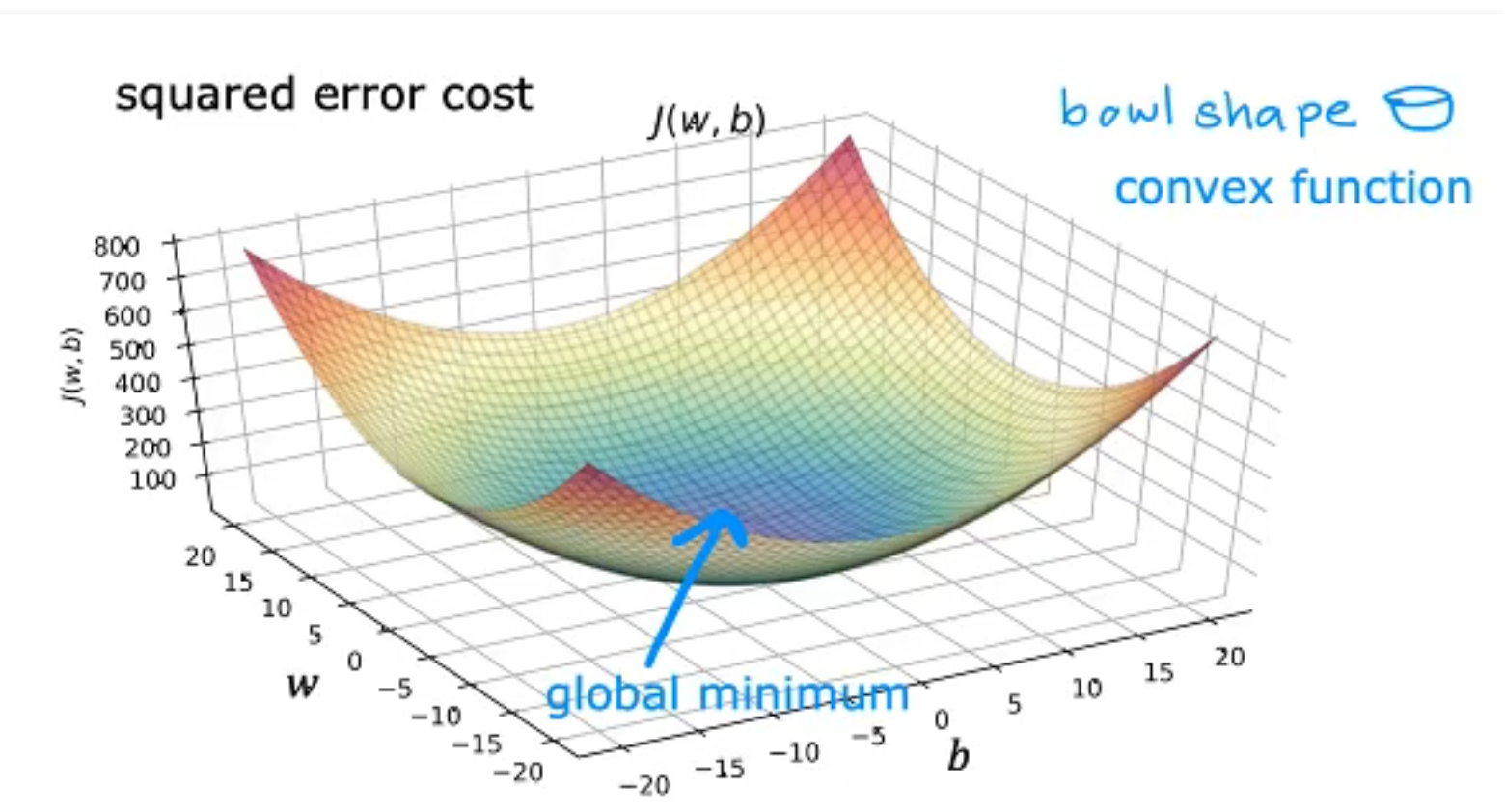
而整个梯度下降法的拟合过程如下所示，

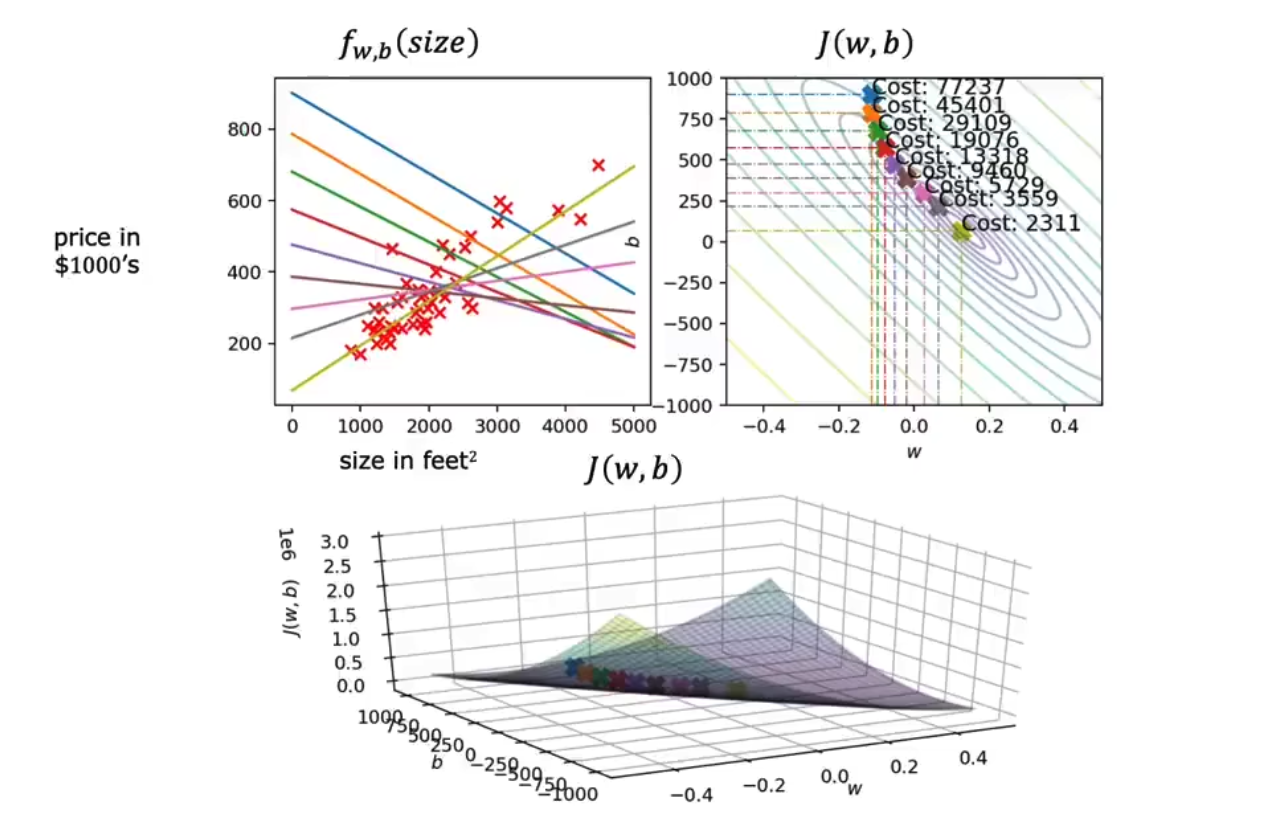
但是往往我们并不会选取全部的数据进行训练，我们会使用一个Batch的数据进行训练，于是有了BGD或者mini-BGD，如下，