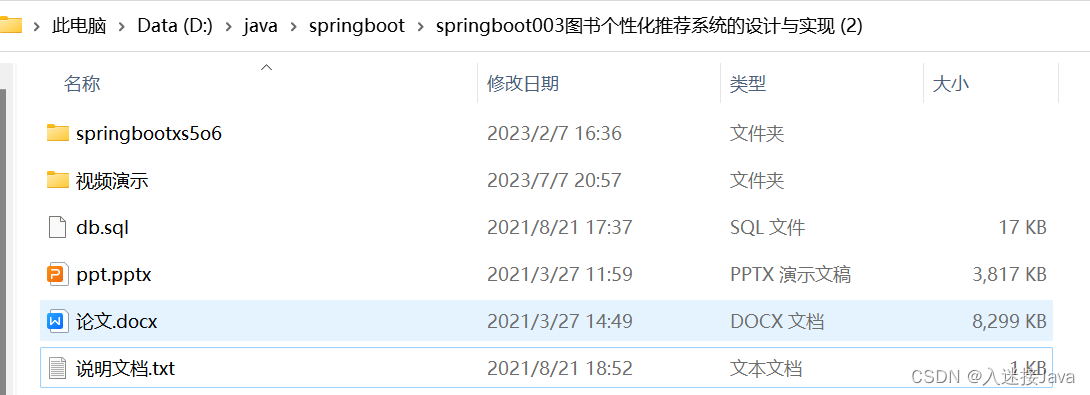
插值法在较少的数据模型的基础上模拟产生新的靠谱数值,可以用来预测。
利用已知的点建立合适的插值函数 f(x) ,未知点 x_i 由插值函数 f(x) 可以求出函数值 f(x_i) ,用求得的 (x_i,f(x_i))近似代替未知点。
基本概念:
y=f(x)在[a,b]上有定义 xi∈[a,b]是有yi与其对应,P(xi)=yi(i=0,1,2……n)
插值函数:P(x)
插值节点:x0,x1,……,xn
插值区间[a,b]
插值法:求插值函数P(x)
插值方法
多项式插值:P(x)为次数不超过n的代数多项式
分段插值:P(x)为分段多项式
三角插值:P(x)为三角多项式(一般用到傅里叶变换)
插值法原理
有n+1个点(x_i,y_i) (i=0,1,2…n)存在唯一多项式:
L_n(x)=a_0 + a_i*x + a_2*x^2 + … + a_n*x^n
使L_n(x_j)=y_j(j=0,1,2…n)
拉格朗日插值法
计算一系列插值基函数:
![]()
利用基函数构造拉格朗日插值多项式:
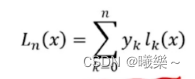
Runge现象
高次插值会产生龙格现象:在两端处波动极大,产生明显震荡。不用高次插值!
分段插值
分段线性插值:函数分段,相近的两个点构成一条线。
分段二次插值:随机选择一点x,找与它相近的三个节点构造二次多项式,进行二次插值。分段抛物线代替y=f(x)。
牛顿插值法
计算过程具有继承性,每次插值只与前n项的值有关,但也存在龙格现象。

![]()
拉格朗日插值和牛顿插值的缺点:龙格现象、不能全面的反映被插值函数的性态(导数不对应)。
埃尔米特(Hermite)插值
函数与被插值函数在所有节点处有相同的函数值,一个或全部节点上插值多项式与被插函数有相同的低阶、高阶导数值(保证插值函数平滑)。

分段三次埃尔米特插值!
MATLAB内置的插值函数pchip
x = -pi:pi; %x横坐标范围(-pi到pi,步长为1)
y = sin(x);%y函数
new_x = -pi:0.1:pi;%新的横坐标new_x(-pi到pi,步长为0.1)
p = pchip(x,y,new_x);%p插值
画图
创建画布:figure(1);
% 在同一个脚本文件里面,要想画多个图,需要给每个图编号,否则只会显示最后一个图
plot(x, y, 'o', new_x, p, 'r--')
plot(x1,y1,x2,y2)
修饰:
线方式: - 实线 :点线 -. 虚点线 - - 波折线
点方式: . 圆点 +加号 * 星号 x形 o小圆
颜色: y黄; r红; g绿; b蓝; w白; k黑; m紫; c青
图标:
LEGEND(string1,string2,string3, …)
分别将字符串1、字符串2、字符串3……标注到图中,每个字符串对应的图标为画图时的图标(修饰)。
‘Location’用来指定标注显示的位置
plot(x,y)%至少输入横坐标和纵坐标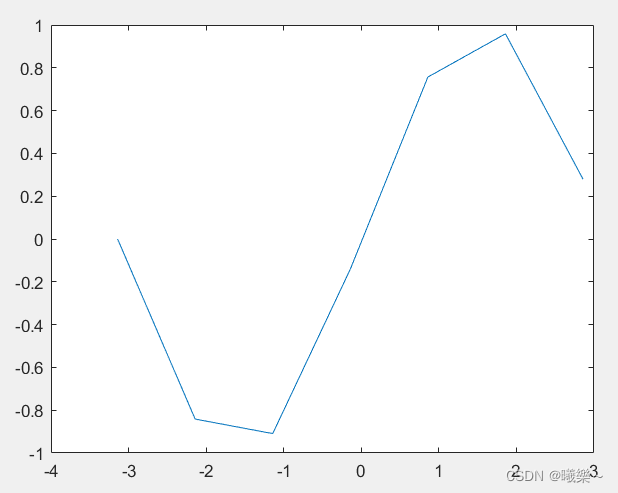
plot(x, y, 'o', new_x, p, 'r--')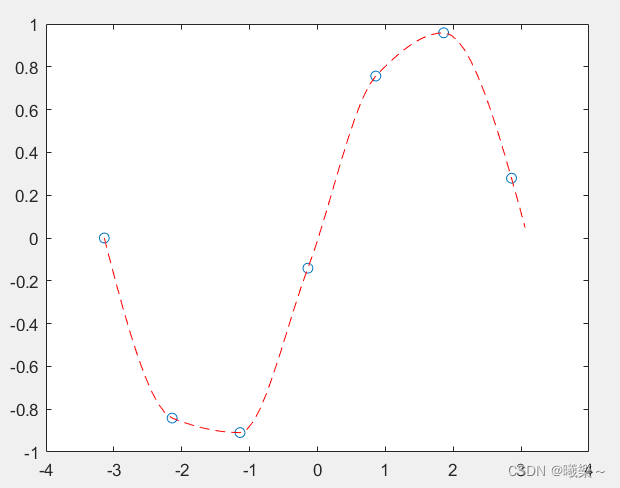
三次样条插值!
二阶连续可微。在每个子区间是三次多项式。最精准
MATLAB内置函数p=spline(x,y,new_x)
与pchip用法一样
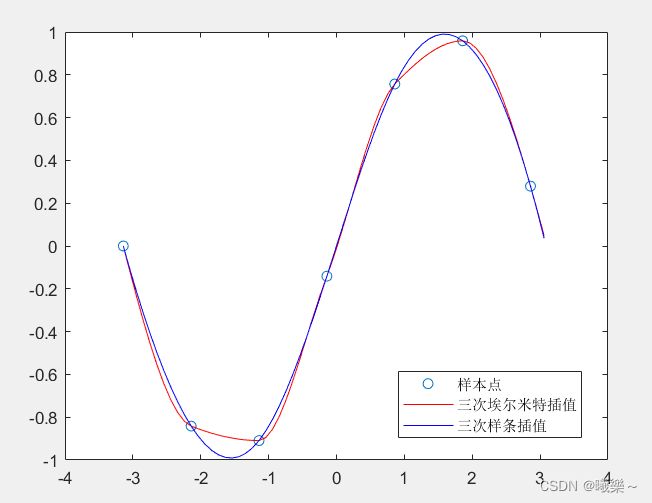
两种插值对比图:
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast') %标注显示在东南方向
%