目录

一、基本概念

Vec是什么？

Vec的特点

(1)动态大小：

(2)可变性：

(3)泛型：

二、基础用法

1. 创建

(1) Vec::new()方法

(2) Vec::from()方法

(3) vec! 宏

2. 基础用法

三、Vec的简单实现及其宏模拟

四、leetcode 实战

1. 长度最小的子数组 Minimum-size-subarray-sum

2. 最大子数组和  Maximum Subarray

3. 螺旋矩阵 Spiral Matrix

---

Rust中的Vec是一种动态数组，它可以在运行时自动调整大小。Vec是Rust标准库的一部分，提供了一种高效、安全的方式来处理大量数据。基于堆内存申请的连续动态数据类型，其索引、压入(push)、弹出(pop) 操作的时间复杂度为 O(1) 。

一、基本概念

Vec是什么？

Vec，是“vector”的缩写。一种动态数组，它可以在运行时自动调整大小。Vec的底层实现是基于数组的，因此它的性能非常高。Vec可以存储任何类型的数据，包括整数、浮点数、字符串等。

Vec其实是一个智能指针，用于在堆上分配内存的动态数组。它提供了一些方法来操作数组，如添加、删除和访问元素。与C或Python中的数组不同，Vec会自动处理内存分配和释放，从而避免了常见的内存泄漏和悬挂指针错误。

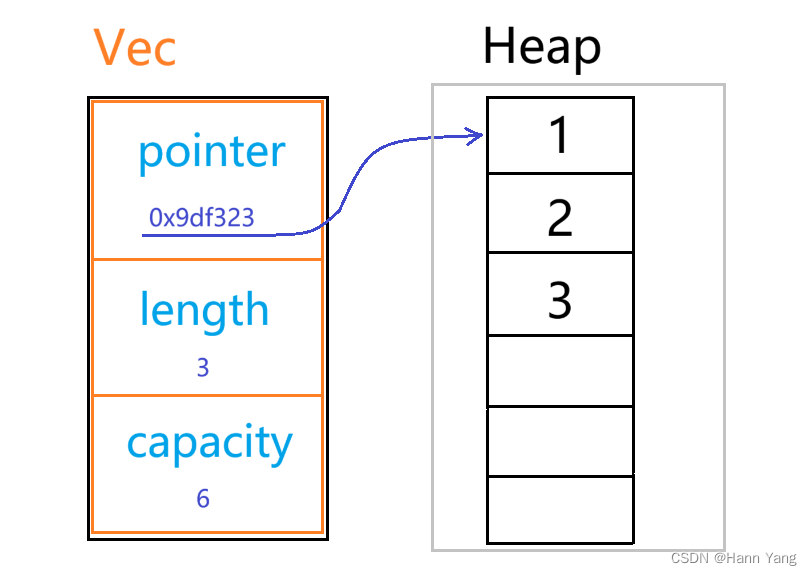
Vec的本质就是一个三元组，指针、长度、容量，在rust标准库中的定义如下：

pub struct Vec<T, A: Allocator = Global> {
    buf: RawVec<T, A>,
    len: usize,
}
impl<T> Vec<T> {
    #[inline]
    pub const fn new() -> Self {
        Vec { buf: RawVec::NEW, len: 0 }
    }
//...略...
}

Vec的核心功能之一是动态增长和收缩。当向Vec中添加元素时，如果堆上的内存不足，Vec会自动分配更多的内存来容纳元素。这个过程称为“扩容”。同样，当从Vec中删除元素时，如果堆上的内存过多，Vec会自动收缩以释放内存。这个过程称为“缩容”。这种自动内存管理机制使得使用Vec变得非常方便，同时也避免了手动管理内存的错误。

除了基本的添加、删除和访问元素操作之外，Vec还提供了许多其他功能。例如，它们可以按索引访问元素，可以使用迭代器遍历元素，并且支持多种方法（如push()、pop()、insert()和remove()）来修改Vec的内容。Vec还提供了一些有用的静态方法（如capacity()、len()和is_empty()），可以用来获取Vec的属性。

虽然Vec是一个非常强大的数据结构，但它们也有一些限制。例如，Vec在堆上分配内存，这意味着访问元素的速度可能会比在栈上分配内存的数组慢。此外，由于Vec是智能指针，因此它们的大小不是固定的，这可能会导致一些编程错误。例如，如果尝试将Vec赋值给一个固定大小的数组或另一个Vec，则会发生编译时错误。

Vec的特点

(1)动态大小：

Vec可以根据需要自动调整大小，无需预先分配内存。当元素数量发生变化时，Vec会自动重新分配内存并复制元素。

(2)可变性：

Vec是可变的，这意味着我们可以在不创建新Vec的情况下修改现有元素。这使得我们在处理大量数据时更加灵活。

(3)泛型：

Vec是泛型的，这意味着我们可以使用相同的方法来处理不同类型的数据。例如，我们可以使用vec![1, 2, 3]创建一个包含整数的Vec,使用vec!["a", "b", "c"]创建一个包含字符串的Vec。

动态数组是一种基于堆内存申请的连续动态数据类型，拥有 O(1) 时间复杂度的索引、压入（push）、弹出（pop)。 

二、基础用法

1. 创建

(1) Vec::new()方法

只创建一个空列表时，必须注明类型（否则通不过编译）。如下例的正确用法：

fn main() {
    let vec: Vec<i32> = Vec::new();
    println!("{:?}", vec);
}

输出：

[] 

注：print!、println!输出Vec时需要使用格式符 "{:?}" 。

但如果下一步要添加元素，比如使用push(x)方法，就非必须注明类型，默认就是 i32 类型：

示例： 

fn main() {
    let mut vec = Vec::new();
    vec.push(1);
    vec.push(2);
    vec.push(3);
    println!("{:?}", vec);
}

输出：

[1, 2, 3]

(2) Vec::from()方法

    let vec = Vec::from([1,2,3]);

(3) vec! 宏

    let vec = vec![1,2,3];

用法示例及判断是否相等：

fn main() {
    let vec1 = Vec::from([1,2,3]);
    println!("{:?}", vec1);
    let vec2 = vec![1,2,3];
    println!("{:?}", vec2);
    assert_eq!(vec1, vec2);
    assert_eq!(vec1, [1,2,3]);
    assert_eq!(vec2, [1,2,3]);
    println!("{}", vec1 == vec2);
}

输出：

[1, 2, 3]
[1, 2, 3]
true

vec! 宏 的另外用法： 

创建 len 个相同元素 n 的Vec，如：vec![n; len]。

示例：

fn main() {
    let vec = vec![0; 5];
    assert_eq!(vec, [0, 0, 0, 0, 0]);
    println!("{:?}", vec);
    let vec = vec![1; 3];
    assert_eq!(vec, [1, 1, 1]);
    println!("{:?}", vec);
    let vec = vec![1; 0];
}

以下是vec![1; 3]的等效方法，但速度较慢：

​fn main() {
    let mut vec = Vec::with_capacity(3);
    vec.resize(3, 1);
    assert_eq!(vec, [1, 1, 1]);
}

以上3种创建方法中，使用第3种方法的vec!宏来创建Vec相对比较方便。

二维Vec的创建和遍历

fn main() {
    // 创建一个2x3的二维向量
    let matrix: Vec<Vec<i32>> = vec![
        vec![1, 2, 3], 
        vec![4, 5, 6]
    ];
    
    // 遍历二维向量
    for row in &matrix {
        for &num in row {
            print!("{} ", num);
        }
        println!();
    }

    // 创建一个3x5的二维向量，所有元素都为 1
    let (m, n) = (3, 5);
    let number = 1;
    let matrix = vec![vec![number; n]; m];
    for row in &matrix {
        for &num in row {
            print!("{} ", num);
        }
        println!();
    }
}

输出：

1 2 3 
4 5 6 
1 1 1 1 1 
1 1 1 1 1 
1 1 1 1 1 

---

2. 基础用法

Vec内置了非常丰富的内置方法，以下方法收集自网络，有重复暂时没空余时间去好好整理。

new(): 创建一个空的 Vec。
with_capacity(capacity: usize): 创建一个具有指定容量的空 Vec。
capacity() -> usize: 返回 Vec 的当前容量。
reserve(new_cap: usize): 为 Vec 分配额外的空间。
reserve_exact(new_cap: usize): 为 Vec 分配精确的额外空间。
shrink_to_fit(): 缩小 Vec 的容量以匹配其当前大小。
len() -> usize: 返回 Vec 的当前长度。
is_empty() -> bool: 检查 Vec 是否为空。
push(value: T): 将一个值添加到 Vec 的末尾。
pop() -> Option<T>: 删除并返回 Vec 的最后一个元素。
insert(index: usize, element: T): 在指定位置插入一个元素。
remove(index: usize) -> T: 删除并返回指定位置的元素。
swap(index1: usize, index2: usize): 交换指定位置上的两个元素。
truncate(len: usize): 将 Vec 截断为指定长度。
clear(): 删除 Vec 中的所有元素。
iter() -> Iter<T>: 返回一个迭代器，它允许按顺序遍历 Vec 中的元素。
iter_mut() -> IterMut<T>: 返回一个可变迭代器，它允许按顺序遍历 Vec 中的元素并进行修改。
into_iter() -> IntoIter<T>: 返回一个迭代器，它允许按顺序遍历 Vec 中的元素并转移所有权。
split_off(at: usize) -> Vec<T>: 从指定位置将 Vec 拆分为两个独立的 Vec。
append(&mut self, other: &mut Vec<T>): 将另一个 Vec 的所有元素附加到当前 Vec 的末尾。

swap(index1: usize, index2: usize): 交换指定位置的两个元素。
get(index: usize) -> Option<&T>: 获取指定位置的元素的引用。
get_mut(index: usize) -> Option<&mut T>: 获取指定位置的元素的可变引用。
first() -> Option<&T>: 获取 Vec 的第一个元素的引用。
first_mut() -> Option<&mut T>: 获取 Vec 的第一个元素的可变引用。
last() -> Option<&T>: 获取 Vec 的最后一个元素的引用。
last_mut() -> Option<&mut T>: 获取 Vec 的最后一个元素的可变引用。
split_at(index: usize) -> (&[T], &[T]): 将 Vec 分成两个部分，从指定位置进行分割。
split_at_mut(index: usize) -> (&mut [T], &mut [T]): 将 Vec 分成两个部分，从指定位置进行分割，返回可变引用。
as_slice() -> &[T]: 将 Vec 转换为切片，返回不可变引用。
as_mut_slice() -> &mut [T]: 将 Vec 转换为切片，返回可变引用。
iter() -> Iter<'_, T>: 返回一个迭代器，用于遍历 Vec 中的元素。
iter_mut() -> IterMut<'_, T>: 返回一个迭代器，用于遍历 Vec 中的元素，并返回可变引用。
into_iter() -> IntoIter<T>: 返回一个迭代器，用于遍历 Vec 中的元素，Vec 在迭代过程中将被移动。
clone_from(other: &Vec<T>): 从另一个 Vec 复制元素到当前 Vec。
truncate(len: usize): 删除 Vec 的尾部元素，直到长度为指定值。
clear(): 删除 Vec 中的所有元素。

as_slice() -> &[T]: 将 Vec 转换为不可变的切片。
as_mut_slice() -> &mut [T]: 将 Vec 转换为可变的切片。
split_first() -> Option<(&T, &[T])>: 返回 Vec 的第一个元素和其余部分的元组。
split_first_mut() -> Option<(&mut T, &mut [T])>: 返回 Vec 的第一个元素和其余部分的可变引用。
split_last() -> Option<(&T, &[T])>: 返回 Vec 的最后一个元素和其余部分的元组。
split_last_mut() -> Option<(&mut T, &mut [T])>: 返回 Vec 的最后一个元素和其余部分的可变引用。
chunks(chunk_size: usize) -> Chunks<'_, T>: 返回一个迭代器，该迭代器按块大小切分 Vec。
chunks_mut(chunk_size: usize) -> ChunksMut<'_, T>: 返回一个迭代器，该迭代器按块大小切分 Vec，并返回可变引用。
windows(window_size: usize) -> Windows<'_, T>: 返回一个迭代器，该迭代器在 Vec 上滑动，返回指定大小的窗口。
iter() -> Iter<'_, T>: 返回一个不可变引用的迭代器，该迭代器遍历 Vec 中的每个元素。
iter_mut() -> IterMut<'_, T>: 返回一个可变引用的迭代器，该迭代器遍历 Vec 中的每个元素。
into_iter() -> IntoIter<T>: 返回一个拥有所有权的迭代器，该迭代器遍历 Vec 中的每个元素。

chunks_exact(chunk_size: usize) -> ChunksExact<'_, T>: 返回一个迭代器，该迭代器按块大小切分 Vec，每个块都是固定大小的。
chunks_exact_mut(chunk_size: usize) -> ChunksExactMut<'_, T>: 返回一个迭代器，该迭代器按块大小切分 Vec，每个块都是固定大小的，并返回可变引用。
windows(window_size: usize) -> Windows<'_, T>: 返回一个迭代器，该迭代器按指定大小滑动窗口遍历 Vec。
iter() -> Iter<'_, T>: 返回一个不可变的迭代器，遍历 Vec 的元素。
iter_mut() -> IterMut<'_, T>: 返回一个可变的迭代器，遍历 Vec 的元素并返回可变引用。
into_iter() -> IntoIter<T>: 返回一个将 Vec 转换为迭代器的方法。
retain<F>(&mut self, f: F)：在保留满足给定谓词的元素的情况下，删除不满足谓词的所有元素。
dedup(&mut self)：删除连续重复的元素。只保留第一个出现的元素，其他的都被删除。

retain<F>(&mut self, f: F)：在保留满足给定谓词的元素的同时，移除不满足谓词的元素。
truncate(len: usize): 将 Vec 的长度截断为指定长度。
dedup(): 移除 Vec 中相邻的重复元素。
dedup_by_key<F>(&mut self, key: F)：使用指定的键函数，移除 Vec 中相邻的具有相同键的元素。
clone_from(&self, source: &[T]): 从指定的 slice 复制元素到 Vec 中。
extend<I>(&mut self, iter: I)：将迭代器中的元素添加到 Vec 的末尾。
extend_from_slice(slice: &[T]): 将 slice 中的元素添加到 Vec 的末尾。
resize(&mut self, new_len: usize, value: T)：将 Vec 的长度更改为指定长度，并使用指定的值填充新元素。
resize_with<F>(&mut self, new_len: usize, f: F)：将 Vec 的长度更改为指定长度，并使用指定的函数填充新元素。
swap_remove(index: usize) -> T：删除并返回指定位置的元素，并用最后一个元素替换它。
truncate(len: usize): 将 Vec 的长度截断为指定长度。

resize_with<F>(&mut self, new_len: usize, f: F)：将 Vec 的长度更改为指定长度，并使用指定的函数生成新元素。
try_reserve(n: usize) -> Result<(), AllocError>：尝试为至少包含指定数量的元素的 Vec 分配空间。
shrink_to_fit(): 缩小 Vec 的容量以匹配其当前长度。
as_ptr() -> *const T：返回 Vec 的指针。
as_mut_ptr() -> *mut T：返回 Vec 的可变指针。
capacity() -> usize：返回 Vec 的容量。
reserve(&mut self, additional: usize)：为 Vec 分配额外的空间。
reserve_exact(&mut self, additional: usize)：为 Vec 分配确切的额外空间。
set_len(&mut self, len: usize)：设置 Vec 的长度，不检查新长度是否小于或大于容量。
into_boxed_slice(self) -> Box<[T]>：将 Vec 转换为包含所有元素的堆分配数组。
into_raw_parts(self) -> (*mut T, usize, usize)：将 Vec 转换为原始指针，长度和容量的三元组。

into_boxed_slice(self) -> Box<[T]>：将 Vec 转换为包含所有元素的 Box<[T]>。
into_raw_parts(self) -> (*mut T, usize, usize)：将 Vec 转换为其原始指针、长度和容量的元组。
from_raw_parts(ptr: *mut T, len: usize, cap: usize) -> Vec<T>：从原始指针、长度和容量的元组创建 Vec。
from_raw_parts_mut(ptr: *mut T, len: usize, cap: usize) -> Vec<T>：从原始指针、长度和容量的元组创建可变的 Vec。
drain<R>(&mut self, range: R) -> Drain<'_, T>：删除指定范围内的元素，并返回一个迭代器，该迭代器遍历已删除的元素。

splice<R, I>(&mut self, range: R, replace_with: I) -> Splice<'_, R::End, I::IntoIter>：将指定范围内的元素替换为迭代器中的元素，并返回一个迭代器，该迭代器遍历已删除的元素。
retain<F>(&mut self, f: F)：在保留满足给定谓词的元素的同时，移除不满足谓词的元素。
partition<F>(&mut self, f: F) -> (Vec<T>, Vec<T>)：根据给定谓词，将 Vec 中的元素分成两个新 Vec。
sort(&mut self)：对 Vec 中的元素进行排序。
sort_by_key<K, F>(&mut self, key: F)：使用指定的键函数，对 Vec 中的元素进行排序。
sort_by<F>(&mut self, compare: F)：使用指定的比较函数，对 Vec 中的元素进行排序。
sort_unstable(): 对 Vec 中的元素进行不稳定排序。
splice<R, I>(&mut self, range: R, replace_with: I) -> Splice<'_, R::End, I::IntoIter>：将指定范围内的元素替换为迭代器中的元素，并返回一个迭代器，该迭代器遍历已删除的元素。
split_off(&mut self, at: usize) -> Vec<T>：将 Vec 拆分为两个 Vec，从指定位置开始拆分。
swap_remove(&mut self, index: usize) -> T：删除指定索引处的元素并返回它。
swap_remove_item(&mut self, item: &T) -> bool：查找并删除第一个等于给定元素的元素，并返回是否找到该元素。
truncate(&mut self, len: usize)：将 Vec 的长度截断为指定长度。
unwrap()：将包装在 Option 中的 Vec 解包，如果是 None，则 panic。
unwrap_or(default: Vec<T>) -> Vec<T>：将包装在 Option 中的 Vec 解包，如果是 None，则返回提供的默认值。
unwrap_or_default() -> Vec<T>：将包装在 Option 中的 Vec 解包，如果是 None，则返回默认值。

unwrap_or(default: Vec<T>) -> Vec<T>：将包装在 Option 中的 Vec 解包，如果是 None，则返回指定的默认值。
unwrap_or_else<F: FnOnce() -> Vec<T>>(f: F) -> Vec<T>：将包装在 Option 中的 Vec 解包，如果是 None，则调用指定的函数生成默认值。
zip<U>(self, other: U) -> Zip<Self, U::IntoIter>：创建一个迭代器，该迭代器通过将 self 和其他迭代器的元素进行配对来生成元组。
iter() -> Iter<'_, T>：返回一个迭代器，该迭代器遍历 Vec 的元素。
iter_mut() -> IterMut<'_, T>：返回一个可变迭代器，该迭代器遍历 Vec 的元素。
into_iter(self) -> IntoIter<T>：将 Vec 转换为其元素的迭代器。
len() -> usize：返回 Vec 的长度。
is_empty() -> bool：如果 Vec 为空，则返回 true，否则返回 false。
last() -> Option<&T>：返回 Vec 的最后一个元素的引用，如果 Vec 为空，则返回 None。
last_mut() -> Option<&mut T>：返回 Vec 的最后一个元素的可变引用，如果 Vec 为空，则返回 None。
split_first(&self) -> Option<(&T, &[T])>：返回 Vec 的第一个元素的引用和剩余元素的 slice，如果 Vec 为空，则返回 None。
split_first_mut(&mut self) -> Option<(&mut T, &mut [T])>：返回 Vec 的第一个元素的可变引用和剩余元素的可变 slice，如果 Vec 为空，则返回 None。

is_empty() -> bool：如果 Vec 为空，则返回 true，否则返回 false。
as_slice(&self) -> &[T]：将 Vec 转换为其元素的切片。
as_mut_slice(&mut self) -> &mut [T]：将 Vec 转换为其元素的可变切片。
last(&self) -> Option<&T>：返回 Vec 的最后一个元素的引用，如果 Vec 为空，则返回 None。
last_mut(&mut self) -> Option<&mut T>：返回 Vec 的最后一个元素的可变引用，如果 Vec 为空，则返回 None。
first(&self) -> Option<&T>：返回 Vec 的第一个元素的引用，如果 Vec 为空，则返回 None。
first_mut(&mut self) -> Option<&mut T>：返回 Vec 的第一个元素的可变引用，如果 Vec 为空，则返回 None。
binary_search(&self, x: &T) -> Result<usize, usize>：在已排序的 Vec 中搜索指定元素，并返回其索引。
sort(&mut self)：按升序对 Vec 的元素进行排序。
sort_by_key<K, F>(&mut self, f: F)：按升序对 Vec 的元素进行排序，其中排序关键字由指定的函数生成。
sort_by<F>(&mut self, compare: F)：按升序对 Vec 的元素进行排序，其中比较函数由指定的函数生成。

binary_search(&self, x: &T) -> Result<usize, usize>：在已排序的 Vec 中搜索指定元素，并返回它的索引。如果元素不存在，则返回 Err，该 Err 包含元素应该插入的位置的索引。
binary_search_by<F>(&self, f: F) -> Result<usize, usize> where F: FnMut(&T) -> Ordering：在已排序的 Vec 中使用指定的比较函数搜索指定元素，并返回它的索引。如果元素不存在，则返回 Err，该 Err 包含元素应该插入的位置的索引。
binary_search_by_key<K, F>(&self, key: &K, f: F) -> Result<usize, usize> where F: FnMut(&T) -> K, K: Ord：在已排序的 Vec 中使用指定的键函数搜索指定键，并返回它的索引。如果键不存在，则返回 Err，该 Err 包含键应该插入的位置的索引。
sort(&mut self)：对 Vec 中的元素进行排序。
sort_by<F>(&mut self, compare: F)：使用指定的比较函数对 Vec 中的元素进行排序。
sort_by_key<K, F>(&mut self, f: F)：使用指定的键函数对 Vec 中的元素进行排序。
reverse(&mut self)：反转 Vec 中元素的顺序。
split_off(&mut self, at: usize) -> Vec<T>：将 Vec 拆分为两个 Vec，从指定位置开始拆分。

chunks(&self, chunk_size: usize) -> Chunks<'_, T>：返回一个迭代器，该迭代器遍历 Vec 的不重叠的块，每个块包含指定数量的元素。
chunks_mut(&mut self, chunk_size: usize) -> ChunksMut<'_, T>：返回一个可变迭代器，该迭代器遍历 Vec 的不重叠的块，每个块包含指定数量的元素。
windows(&self, window_size: usize) -> Windows<'_, T>：返回一个迭代器，该迭代器遍历 Vec 的连续窗口，每个窗口包含指定数量的元素。
try_fold<B, F, R>(&self, init: B, f: F) -> R where F: FnMut(B, &T) -> Result<B, R>, R: From<B>：对 Vec 中的每个元素执行指定的操作，并返回结果。如果任何操作返回 Err，则停止并返回 Err，否则返回 Ok。
try_for_each<F, R>(&self, f: F) -> R where F: FnMut(&T) -> Result<(), R>, R: From<()>：对 Vec 中的每个元素执行指定的操作，并返回结果。如果任何操作返回 Err，则停止并返回 Err，否则返回 Ok。

try_for_each<F, R>(&self, f: F) -> R where F: FnMut(&T) -> Result<(), R>, R: From<()>：对 Vec 中的每个元素执行指定的操作，并返回结果。如果任何操作返回 Err，则停止并返回 Err，否则返回 Ok。
contains(&self, x: &T) -> bool：如果 Vec 包含指定的元素，则返回 true，否则返回 false。
dedup(&mut self)：删除 Vec 中的重复元素。只保留第一次出现的元素。
dedup_by_key<F>(&mut self, key: F)：删除 Vec 中的重复元素。只保留第一次出现的元素。比较是使用指定的键函数进行的。
retain<F>(&mut self, f: F)：从 Vec 中删除不满足指定条件的所有元素。
split_off(&mut self, at: usize) -> Vec<T>：从 Vec 中分离指定索引之后的所有元素，并返回一个新的 Vec。
truncate(&mut self, len: usize)：将 Vec 的长度截断为指定长度。如果指定长度小于 Vec 的当前长度，则删除多余的元素。

---

三、Vec的简单实现及其宏模拟

trait MyVec {
    type Item;
    fn new() -> Self;
    fn len(&self) -> usize;
    fn push(&mut self, element: Self::Item);
    fn pop(&mut self) -> Option<Self::Item>;
}

impl<T> MyVec for Vec<T> {
    type Item = T;

    fn new() -> Vec<T> {
        Vec::new()
    }

    fn len(&self) -> usize {
        Vec::len(self)
    }

    fn push(&mut self, element: T) {
        Vec::push(self, element)
    }
    
    fn pop(&mut self) -> Option<T> {
        Vec::pop(self)
    }
}

macro_rules! myvec {
    ( $( $x:expr ),* ) => {
        {
            let mut vec = <Vec<_> as MyVec>::new();
            $(
                vec.push($x);
            )*
            vec
        }
    };
}

fn main() {
    let mut v = myvec![1,2,3,4];
    println!("{:?}, size = {}", v, v.len());
    
    if let Some(last) = v.pop() {   // 检查向量是否为空
        println!("弹出的尾部元素: {:?}", last);
        println!("{:?}, size = {}", v, v.len());
    } else {
        println!("Vector is empty");  // 向量为空的情况
    }

    v.push(5);
    println!("{:?}, size = {}", v, v.len());
}

输出：

[1, 2, 3, 4], size = 4
弹出的尾部元素: 4
[1, 2, 3], size = 3
[1, 2, 3, 5], size = 4

---

四、leetcode 实战

1. 长度最小的子数组 Minimum-size-subarray-sum

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

提示：

1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5

代码1：

fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
    let mut i = 0;
    let mut j = 0;
    let mut sum = 0;
    let mut min_len = std::usize::MAX;
    while j < nums.len() {
        sum += nums[j];
        j += 1;
        while sum >= target {
            min_len = min_len.min(j - i);
            sum -= nums[i];
            i += 1;
        }
    }
    if min_len == std::usize::MAX {
        0
    } else {
        min_len as i32
    }
}

fn main() {
    let nums = vec![2, 3, 1, 2, 4, 3];
    println!("{}", min_sub_array_len(7, nums));
    let nums = vec![1, 4, 4];
    println!("{}", min_sub_array_len(4, nums));
}

代码2：

fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
    let mut min_len = i32::MAX;
    let (mut left, mut right) = (0, 0);
    let mut sum = 0;
    while right < nums.len() {
        sum += nums[right];
        while sum >= target {
            min_len = min(min_len, (right - left + 1) as i32);
            sum -= nums[left];
            left += 1;
        }
        right += 1;
    }
    if min_len == i32::MAX {
        return 0;
    }
    min_len
}
    
fn min(a: i32, b: i32) -> i32 {
    if a < b {
        a
    } else {
        b
    }
}

fn main() {
    let nums = vec![2, 3, 1, 2, 4, 3];
    println!("{}", min_sub_array_len(7, nums));
    let nums = vec![1, 4, 4];
    println!("{}", min_sub_array_len(4, nums));
}

2. 最大子数组和  Maximum Subarray

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

代码1： 动态规划

fn max_sub_array(nums: &[i32]) -> i32 {
    let n = nums.len();
    let mut dp = vec![0; n];
    dp[0] = nums[0];
    for i in 1..n {
        dp[i] = std::cmp::max(dp[i-1] + nums[i], nums[i]);
    }
    let mut res = dp[0];
    for i in 1..n {
        res = std::cmp::max(res, dp[i]);
    }
    res
}

fn main() {
    let nums = vec![-2, 1, -3, 4, -1, 2, 1, -5, 4];
    println!("{}", max_sub_array(&nums));
    let nums = vec![1];
    println!("{}", max_sub_array(&nums));
    let nums = vec![5,4,-1,7,8];
    println!("{}", max_sub_array(&nums));
}

代码2： 贪心算法

fn max_sub_array(nums: &[i32]) -> i32 {
    let n = nums.len();
    let (mut cur_sum, mut max_sum) = (0, nums[0]);
    for i in 0..n {
        cur_sum += nums[i];
        if cur_sum > max_sum {
            max_sum = cur_sum;
        }
        if cur_sum < 0 {
            cur_sum = 0;
        }
    }
    max_sum
}

fn main() {
    let nums = vec![-2, 1, -3, 4, -1, 2, 1, -5, 4];
    println!("{}", max_sub_array(&nums));
    let nums = vec![1];
    println!("{}", max_sub_array(&nums));
    let nums = vec![5,4,-1,7,8];
    println!("{}", max_sub_array(&nums));
}

输出：

6
1
23

---

3. 螺旋矩阵 Spiral Matrix

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

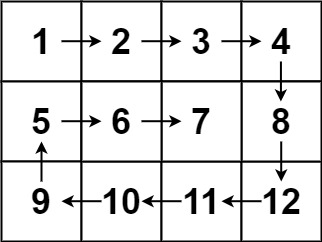
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

代码1：

fn spiral_order(matrix: &[Vec<i32>]) -> Vec<i32> {
    if matrix.is_empty() {
        return vec![];
    }
    let (m, n) = (matrix.len(), matrix[0].len());
    let mut res = vec![0; m * n];
    let (mut top, mut bottom, mut left, mut right) = (0, m - 1, 0, n - 1);
    let mut idx = 0;
    while top <= bottom && left <= right {
        for i in left..=right {
            res[idx] = matrix[top][i];
            idx += 1;
        }
        for i in top + 1..=bottom {
            res[idx] = matrix[i][right];
            idx += 1;
        }
        if top < bottom && left < right {
            for i in (left..right).rev() {
                res[idx] = matrix[bottom][i];
                idx += 1;
            }
            for i in (top + 1..=bottom - 1).rev() {
                res[idx] = matrix[i][left];
                idx += 1;
            }
        }
        top += 1;
        bottom -= 1;
        left += 1;
        right -= 1;
    }
    res
}

fn main() {
    let matrix = vec![
        vec![1, 2, 3],
        vec![4, 5, 6],
        vec![7, 8, 9],
    ];
    println!("{:?}", spiral_order(&matrix));
    let matrix = vec![
        vec![1, 2, 3, 4],
        vec![5, 6, 7, 8],
        vec![9,10,11,12],
    ];
    println!("{:?}", spiral_order(&matrix));
}

代码2： 递归

fn spiral_order(matrix: Vec<Vec<i32>>) -> Vec<i32> {
    fn spiral_helper(top: usize, bottom: usize, left: usize, right: usize, res: &mut Vec<i32>, idx: &mut usize, matrix: &Vec<Vec<i32>>) {
        if top > bottom || left > right {
            return;
        }
        
        // 从左到右遍历上边界
        for i in left..=right {
            res[*idx] = matrix[top][i];
            *idx += 1;
        }
        
        // 从上到下遍历右边界
        for i in (top + 1)..=bottom {
            res[*idx] = matrix[i][right];
            *idx += 1;
        }
        
        if top < bottom && left < right {
            // 从右到左遍历下边界
            for i in (left..right).rev() {
                res[*idx] = matrix[bottom][i];
                *idx += 1;
            }
            
            // 从下到上遍历左边界
            for i in ((top + 1)..bottom).rev() {
                res[*idx] = matrix[i][left];
                *idx += 1;
            }
        }
        
        // 矩形边界变小，递归调用spiral_helper继续遍历
        spiral_helper(top + 1, bottom - 1, left + 1, right - 1, res, idx, matrix);
        
    }
    
    let m = matrix.len();
    let n = matrix[0].len();
    let mut res = vec![0; m * n]; // 用于记录遍历结果
    let mut idx = 0; // 当前结果数组的下标
    
    // 从矩形最外层开始遍历
    spiral_helper(0, m - 1, 0, n - 1, &mut res, &mut idx, &matrix);
    
    res
}

fn main() {
    let matrix = vec![
        vec![1, 2, 3],
        vec![4, 5, 6],
        vec![7, 8, 9],
    ];
    println!("{:?}", spiral_order(matrix));
    
    let matrix = vec![
        vec![1, 2, 3, 4],
        vec![5, 6, 7, 8],
        vec![9,10,11,12],
    ];
    println!("{:?}", spiral_order(matrix));
}

输出：

[1, 2, 3, 6, 9, 8, 7, 4, 5]
[1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7] 

---

完