最大流?费用流？结合二分图？例题

最大流

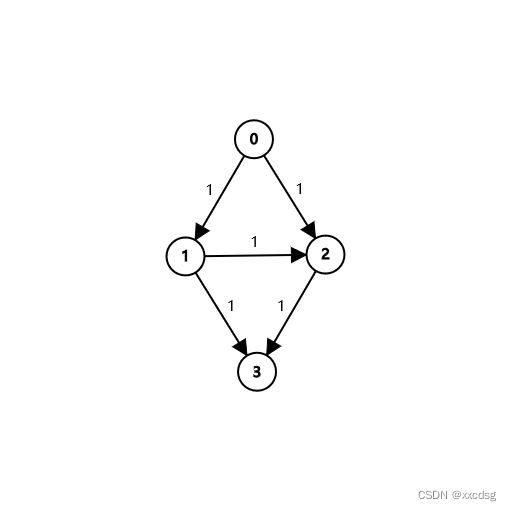
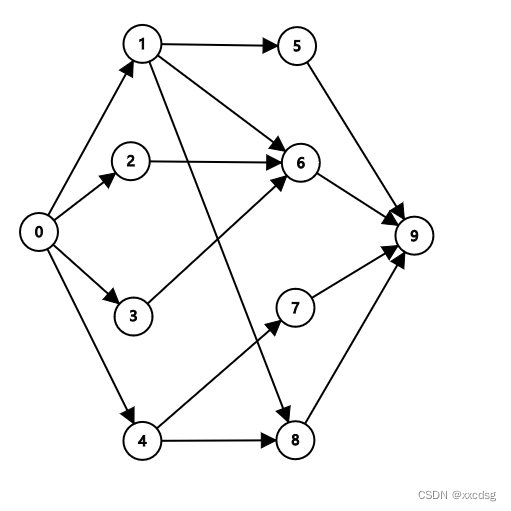
给出起点，终点，与边，边有最大流量限制，问从起点在不超过边的流量限制的情况下最大能从起点流多少流量到终点
反悔思想：如果我们每次找到一条路径就把这条路径上流量最小的边删去直到没有路径连接起点和终点，这就形成了一个阻塞流（不能再给终点增加值的流），虽然最大流是阻塞流，但阻塞流不一定是最大流，下面来个例子

就比如这张图，我们可以很容易看出该图的最大流为2，但如果我们取 $0 - > 1 - > 2 - > 3$ 这条路径，那么得出的阻塞流就为1，也就是说我们取的路径有可能阻塞了其他的路径导致取少
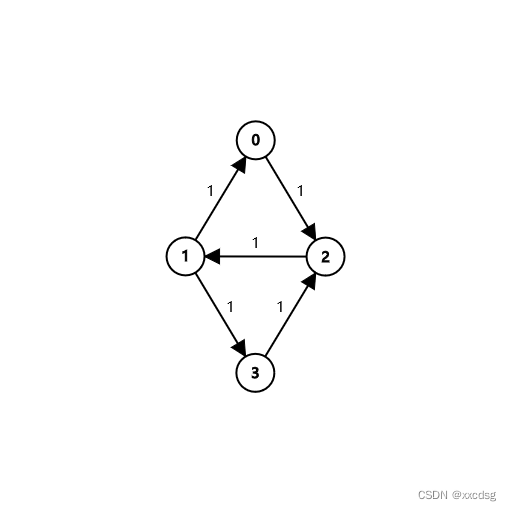
那么该怎么解决呢，我们引入反向边的概念
比如我们像刚刚那么取，但是引入反向边，那么图就变成
我们可以发现该图并没有变成阻塞流，还可以取 $0 - > 2 - > 1 - > 3$ 这条路径，让我们再取

请添加图片描述

现在该图变成了阻塞流，而我们得到的最大流也就是2，因此引入反向边再让它完全变成阻塞流这种做法同理在其他图中也可以得到最大流

建图

struct edge{
	int v,w;
	edge* nex;
	int i;//在回溯时记录边
}ed[MAXM*2];
void add(int u,int v,int w){
	ed[ptop].w = w;
	ed[ptop].v = v;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
	ed[ptop].w = 0;
	ed[ptop].v = u;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];//构造反向边
	ed[ptop].i = ptop;
	ptop++;
}

那么怎么找阻塞流呢？
Ford-Fulkerson算法（就dfs找一条路，复杂度取决于边的权值和，不可取）
Edmonds-Karp算法（找最短路，一般用SPFA找，因为可能有负权边，~~用dijkstra+势函数我不会~~ ）
Dinic算法（每次都用bfs造个分层图，然后反着用dfs把能取的路径全取了，一次能取多条路径）

Edmonds-Karp算法

需要两个部分：SAP找可行最短路径与根据最短路径更新图
SAP

int pre[MAXN*2],use[MAXN];
bool find(){
	memset(use,0,sizeof(use));//初始化
	use[s] = 1;//标记起点
	queue<int> qu;qu.push(s);//起点
	while(!qu.empty()){
		int x = qu.front();
		qu.pop();
		for(edge* p = head[x];p != NULL;p = p -> nex){
			int v = p -> v;
			if(use[v] || p -> val == 0)//没找过并且有边可行
				continue;
			pre[v] = p -> i;//记录这条边
			use[v] = 1;
			if(v == t)//如果是终点就停止
				return 1;
			qu.push(v);
		}
	}
	return 0;//没找到
}

更新

void EK(){
	while(find()){//一直找直到没有
		ll mi = (ll)1 << 50;//记录路径最小的流量
		for(int i = pre[t];i != 0;i = pre[ed[i^1].v]){//非常酷，因为反向边的终点就是原来边的起点，而反向边id就是原来边id^1
			mi = min(mi,ed[i].val);
		}
		for(int i = pre[t];i != 0;i = pre[ed[i^1].v]){//更新图
			ed[i].val -= mi;
			ed[i^1].val += mi;
		}
		ans += mi;
	}
}

然后是万众瞩目的Dinic算法
我们需要三部分（只要是两部分）：bfs建新分层图，dfs更新图，Dinic函数
bfs

int d[MAXN];//记录深度
bool bfs(){//构造levelup图
	queue<int> qu;
	memset(d,-1,sizeof(d));
	d[s] = 0;
	qu.push(s);//放入起点
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		edge* p = head[u];
		while(p != NULL){
			int v = p -> v;
			if(p -> w && d[v] == -1){//存在且还没加入图
				d[v] = d[u] + 1;
				qu.push(v);
			}
			p = p -> nex;
		}
	}
	if(d[t] == -1)//到不了终点
		return 0;
	else
		return 1;
}

ll dfs(int u,ll flow){//用递归来找阻塞流
	if(u == t)//到终点了就返回这个流
		return flow;
	edge* p = head[u];
	ll use = 0;
	while(p != NULL){
		int v = p -> v;
		if(d[v] == d[u] + 1 && p -> w){
			ll tem = dfs(v,min(flow,p -> w));//取最小的流继续
			flow -= tem;//减去用去的流继续
			ed[p -> i].w -= tem;
			ed[(p -> i) ^ 1].w += tem;
			use += tem;
			if(flow == 0)
				break;
		}
		p = p -> nex;
	}
	if(use == 0) d[u] = -1;
	return use;
}

Dinic

ll dinic(){
	ll ans = 0;
	while(bfs()){
		ans += dfs(s,inf);
	}
	return ans;
}

费用流：在最大流中找最小费用

EK本来找路径是最短路，那么我们改成最小费用路即可
【模板】最小费用最大流

#include<bits/stdc++.h>
using namespace std;

const int N = 5e4 + 10,M = 5e5 + 10,INF = 0x7f7f7f7f;
int n,m,s,t,ans1,ans2;

struct edge{
	int v,flow,cost,i;
	edge* nex;
}ed[M];
int ptop = 0;
edge* head[N];
void add(int u,int v,int flow,int cost){
	ed[ptop].v = v;
	ed[ptop].flow = flow;
	ed[ptop].cost = cost;
	ed[ptop].i = ptop;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ptop++;
	ed[ptop].v = u;
	ed[ptop].flow = 0;
	ed[ptop].cost = -cost;
	ed[ptop].i = ptop;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];
	ptop++;
}

int pre[M],newcost[N],Flow[N];
bool vis[N];

inline bool spfa(){
	queue<int> qu;qu.push(s);vis[s] = 1;
	memset(Flow,0,sizeof(Flow));Flow[s] = INF;
	memset(newcost,INF,sizeof(newcost));newcost[s] = 0;
	memset(pre,0,sizeof(pre));
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		vis[u] = 0;
		for(auto* p = head[u];p != NULL;p = p -> nex){
			int v = p -> v;
			if(p -> flow > 0 && newcost[v] > newcost[u] + p -> cost){
				newcost[v] = newcost[u] + p -> cost;
				Flow[v] = min(Flow[u],p -> flow);
				pre[v] = p -> i;
				if(!vis[v]){vis[v] = 1,qu.push(v);}
			}
		}
	}
	return newcost[t] != INF;
}

void EK(){
	while(spfa()){
		ans1 += Flow[t],ans2 += newcost[t]*Flow[t];
		int u = t;
		while(u != s){
			int k = pre[u];
			ed[k].flow -= Flow[t];
			ed[k^1].flow += Flow[t];
			u = ed[k^1].v;
		}
	}
}

int main(){
	cin >> n >> m >> s >> t;
	for(int i = 1;i <= m;i++){
		int u,v,flow,cost;
		cin >> u >> v >> flow >> cost;
		add(u,v,flow,cost);
	}
	EK();
	cout << ans1 << ' ' << ans2 << endl;
}

利用最大流解决二分图最大匹配

请添加图片描述

我们添加一个0起点与9终点，然后让所有边权值为1跑最大流即可

P2756 飞行员配对方案问题

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e3 + 20,MAXE = 5e4 + MAXN;
#define inf 0x3f3f3f3f
struct edge{
	int u,v,w;
	int i;
	edge* nex;
	bool f;//正常边
}ed[MAXE*2];
edge* head[MAXN];
int ptop = 0;
void add(int u,int v){
	ed[ptop].u = u;
	ed[ptop].v = v;
	ed[ptop].w = 1;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
	ed[ptop].v = u;
	ed[ptop].u = v;
	ed[ptop].w = 0;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
}
int d[MAXN];
int s = 0,t;
bool bfs(){
	queue<int> qu;
	qu.push(s);
	memset(d,-1,sizeof(d));
	d[s] = 0;
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		edge* p = head[u];
		while(p != NULL){
			int v = p -> v;
			if(p -> w && d[v] == -1){
				d[v] = d[u] + 1;
				qu.push(v);
			}
			p = p -> nex;
		}
	}
	if(d[t] == -1)
		return 0;
	else
		return 1;
}
int dfs(int u,int flow){
	edge* p = head[u];
	if(u == t)
		return flow;
	int use = 0;
	while(p != NULL){
		int v = p -> v;
		if(d[v] == d[u] + 1 && p -> w){
			int tem = dfs(v,min(flow,p -> w));
			use += tem;
			flow -= tem;
			ed[p -> i].w -= tem;
			ed[(p -> i)^1].w += tem;
			if(flow == 0)
				break;
		}
		p = p -> nex;
	}
	if(use == 0)
		d[u] = -1;
	return use;
}
int dinic(){
	int ans = 0;
	while(bfs()){
		ans += dfs(s,inf);
	}
	return ans;
}
int main()
{
	int n,m;cin >> m >> n;
	n -= m;
	for(int i = 1;i <= m;i++)//原点
		add(s,i);
	t = n + m + 1;
	for(int i = 1 + m;i < t;i++)//终点
		add(i,t);
	int u,v;
	while(cin >> u >> v)
	{
		if(u == -1)
			break;
		add(u,v);
		ed[ptop - 2].f = 1;
	}
	cout << dinic() << endl;
	for(int i = 1;i <= ptop;i++){
		if(ed[i].w == 0 && ed[i].f)
			cout << ed[i].u << ' ' << ed[i].v << endl;
	}
}

最大流中让最大边流量最小

二分限制边大小跑dinic，如果与无限制相同说明可行，继续限制

P3305 [SDOI2013] 费用流(假费用流题)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
const int MAXN = 201,MAXM = 5e3 + 10;
const double eps = 1e-8;
struct edge{
	int v;
	double w,_w;
	edge* nex;
	int i;
}ed[MAXM*2];
edge* head[MAXN];
int ptop = 0;
void add(int u,int v,double w){
	ed[ptop].w = w;
	ed[ptop]._w = w;
	ed[ptop].v = v;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
	ed[ptop].w = 0;
	ed[ptop]._w = 0;
	ed[ptop].v = u;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];//构造反向边
	ed[ptop].i = ptop;
	ptop++;
}
int n,m,s,t;
int d[MAXN];//记录深度
bool bfs(){//构造levelup图
	queue<int> qu;
	memset(d,-1,sizeof(d));
	d[s] = 0;
	qu.push(s);//放入起点
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		edge* p = head[u];
		while(p != NULL){
			int v = p -> v;
			if((p -> w > eps) && d[v] == -1){//存在且还没加入图
				d[v] = d[u] + 1;
				qu.push(v);
			}
			p = p -> nex;
		}
	}
	if(d[t] == -1)//到不了终点
		return 0;
	else
		return 1;
}
double dfs(int u,double flow){
	if(u == t)
		return flow;
	edge* p = head[u];
	double use = 0;
	while(p != NULL){
		int v = p -> v;
		if(d[v] == d[u] + 1 && p -> w){
			double tem = dfs(v,min(flow,p -> w));
			flow -= tem;
			ed[p -> i].w -= tem;
			ed[(p -> i) ^ 1].w += tem;
			use += tem;
			if(flow == 0)
				break;
		}
		p = p -> nex;
	}
	if(fabs(use) < eps) d[u] = -1;
	return use;
}
double dinic(){
	double ans = 0;
	bool f = bfs();
	while(f){
		ans += dfs(s,inf);
		f = bfs();
	}
	return ans;
}
double lim;
void init(){
	for(int i = 0;i <= ptop;i++)
		ed[i].w = min(ed[i]._w,lim);
}
double p;
int main()
{
	cin >> n >> m >> p;
	s = 1,t = n;
	for(int i = 1;i <= m;i++){
		int u,v,w;cin >> u >> v >> w;
		add(u,v,w);
	}
	double st = dinic();
	double l = 0,r = 5e4;
	double ans = 0;
	while((r - l) > eps){
		lim = (l + r) / 2;
		init();
		double no = dinic();
		if(fabs(no - st) < eps){
			ans = lim * p;
			r = lim;
		}else{
			l = lim;
		}
	}
	printf("%d\n%.4lf",(int)st,ans);
}

二分限制的二部图最大流(瞎起名是吧 )

P3324 [SDOI2015] 星际战争

题意：N个机器人与M个激光武器，给出每个激光武器每秒的伤害，机器人的血量，每个激光武器能攻击到的机器人，问打爆所有机器人需要的最小时间

思路：对于特定的时间，激光武器能给出的输出总量不同，将它看作起点到激光武器的流量，在特定时间对应的流量能够使得到终点的流量保持最大值那么说明该时间能够将所有机器人打爆，否则不能，然后二分即可

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 201,MAXM = 5e3 + 10;
const double eps = 1e-8,inf = 1e9 + 10;
struct edge{
	int v;
	double w,_w;
	edge* nex;
	int i;
}ed[MAXM*2];
edge* head[MAXN];
int ptop = 0;
void add(int u,int v,double w){
	ed[ptop].w = w;
	ed[ptop]._w = w;
	ed[ptop].v = v;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
	ed[ptop].w = 0;
	ed[ptop]._w = 0;
	ed[ptop].v = u;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];//构造反向边
	ed[ptop].i = ptop;
	ptop++;
}
int n,m,s,t;
int d[MAXN];//记录深度
bool bfs(){//构造levelup图
	queue<int> qu;
	memset(d,-1,sizeof(d));
	d[s] = 0;
	qu.push(s);//放入起点
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		edge* p = head[u];
		while(p != NULL){
			int v = p -> v;
			if((p -> w > eps) && d[v] == -1){//存在且还没加入图
				d[v] = d[u] + 1;
				qu.push(v);
			}
			p = p -> nex;
		}
	}
	if(d[t] == -1)//到不了终点
		return 0;
	else
		return 1;
}
double dfs(int u,double flow){
	if(u == t)
		return flow;
	edge* p = head[u];
	double use = 0;
	while(p != NULL){
		int v = p -> v;
		if(d[v] == d[u] + 1 && p -> w){
			double tem = dfs(v,min(flow,p -> w));
			flow -= tem;
			ed[p -> i].w -= tem;
			ed[(p -> i) ^ 1].w += tem;
			use += tem;
			if(flow == 0)
				break;
		}
		p = p -> nex;
	}
	if(fabs(use) < eps) d[u] = -1;
	return use;
}
double dinic(){
	double ans = 0;
	bool f = bfs();
	while(f){
		ans += dfs(s,inf);
		f = bfs();
	}
	return ans;
}
double tim,a[MAXN],b[MAXN];
void init(){
	for(int i = 0;i <= 2*n - 2;i += 2){
		ed[i].w = tim * a[(i + 2) / 2];
		ed[i^1].w = 0;
	}
	for(int i = 2*n;i <= ptop;i++){
		ed[i].w = ed[i]._w;
	}
}
int main()
{
	cin >> n >> m;
	swap(n,m);
	for(int i = 1;i <= m;i++)
		cin >> b[i];
	for(int i = 1;i <= n;i++)
		cin >> a[i];
	s = 0,t = n + m + 1;
	for(int i = 1;i <= n;i++){
		//cin >> a[i];
		add(s,i,inf);
	}
	for(int i = 1;i <= m;i++){
		//cin >> b[i];
		add(i + n,t,b[i]);
	}
	for(int i = 1;i <= n;i++)
	for(int j = 1;j <= m;j++){
		int op;cin >> op;
		if(op)
			add(i,j + n,inf);
	}
	double all = dinic();
	double l = 0,r = 5e4;
	while(fabs(r - l) > eps){
		tim = (l + r) / 2;
		init();
		if(fabs(dinic() - all) < eps){
			r = tim;
		}else
			l = tim;
	}
	printf("%.4lf",l);
}

最大流板子题

【模板】网络最大流

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
const int MAXN = 201,MAXM = 5e3 + 10;
struct edge{
	int v;
	ll w;
	edge* nex;
	int i;
}ed[MAXM*2];
edge* head[MAXN];
int ptop = 0;
void add(int u,int v,ll w){
	ed[ptop].w = w;
	ed[ptop].v = v;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ed[ptop].i = ptop;
	ptop++;
	ed[ptop].w = 0;
	ed[ptop].v = u;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];//构造反向边
	ed[ptop].i = ptop;
	ptop++;
}
int n,m,s,t;
int d[MAXN];//记录深度
bool bfs(){//构造levelup图
	queue<int> qu;
	memset(d,-1,sizeof(d));
	d[s] = 0;
	qu.push(s);//放入起点
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		edge* p = head[u];
		while(p != NULL){
			int v = p -> v;
			if(p -> w && d[v] == -1){//存在且还没加入图
				d[v] = d[u] + 1;
				qu.push(v);
			}
			p = p -> nex;
		}
	}
	if(d[t] == -1)//到不了终点
		return 0;
	else
		return 1;
}
ll dfs(int u,ll flow){
	if(u == t)
		return flow;
	edge* p = head[u];
	ll use = 0;
	while(p != NULL){
		int v = p -> v;
		if(d[v] == d[u] + 1 && p -> w){
			ll tem = dfs(v,min(flow,p -> w));
			flow -= tem;
			ed[p -> i].w -= tem;
			ed[(p -> i) ^ 1].w += tem;
			use += tem;
			if(flow == 0)
				break;
		}
		p = p -> nex;
	}
	if(use == 0) d[u] = -1;
	return use;
}
ll dinic(){
	ll ans = 0;
	while(bfs()){
		ans += dfs(s,inf);
	}
	return ans;
}
int main()
{
	cin >> n >> m >> s >> t;
	for(int i = 1;i <= m;i++){
		int u,v,w;cin >> u >> v >> w;
		add(u,v,w);
	}
	cout << dinic();
}

费用流板子题

【模板】最小费用最大流

#include<bits/stdc++.h>
using namespace std;

const int N = 5e4 + 10,M = 5e5 + 10,INF = 0x7f7f7f7f;
int n,m,s,t,ans1,ans2;

struct edge{
	int v,flow,cost,i;
	edge* nex;
}ed[M];
int ptop = 0;
edge* head[N];
void add(int u,int v,int flow,int cost){
	ed[ptop].v = v;
	ed[ptop].flow = flow;
	ed[ptop].cost = cost;
	ed[ptop].i = ptop;
	ed[ptop].nex = head[u];
	head[u] = &ed[ptop];
	ptop++;
	ed[ptop].v = u;
	ed[ptop].flow = 0;
	ed[ptop].cost = -cost;
	ed[ptop].i = ptop;
	ed[ptop].nex = head[v];
	head[v] = &ed[ptop];
	ptop++;
}

int pre[M],newcost[N],Flow[N];
bool vis[N];

inline bool spfa(){
	queue<int> qu;qu.push(s);vis[s] = 1;
	memset(Flow,0,sizeof(Flow));Flow[s] = INF;
	memset(newcost,INF,sizeof(newcost));newcost[s] = 0;
	memset(pre,0,sizeof(pre));
	while(!qu.empty()){
		int u = qu.front();
		qu.pop();
		vis[u] = 0;
		for(auto* p = head[u];p != NULL;p = p -> nex){
			int v = p -> v;
			if(p -> flow > 0 && newcost[v] > newcost[u] + p -> cost){
				newcost[v] = newcost[u] + p -> cost;
				Flow[v] = min(Flow[u],p -> flow);
				pre[v] = p -> i;
				if(!vis[v]){vis[v] = 1,qu.push(v);}
			}
		}
	}
	return newcost[t] != INF;
}

void EK(){
	while(spfa()){
		ans1 += Flow[t],ans2 += newcost[t]*Flow[t];
		int u = t;
		while(u != s){
			int k = pre[u];
			ed[k].flow -= Flow[t];
			ed[k^1].flow += Flow[t];
			u = ed[k^1].v;
		}
	}
}

int main(){
	cin >> n >> m >> s >> t;
	for(int i = 1;i <= m;i++){
		int u,v,flow,cost;
		cin >> u >> v >> flow >> cost;
		add(u,v,flow,cost);
	}
	EK();
	cout << ans1 << ' ' << ans2 << endl;
}