今天和大家分享一个令人着迷的数学谜题——冰雹猜想。这个谜题曾在1976年引起轰动，当时《华盛顿邮报》以头版头条刊登了一篇关于它的报道。让我们一起探索这个数学游戏的奥秘。

        70年代中期，美国一所名牌大学的校园内兴起了一种数学游戏，这个游戏看似简单，却让人们沉迷其中。游戏规则很简单：任意写出一个（非零）自然数N，并按照以下规律进行变换。

• 如果N是奇数，则将其变为3N+1；
• 如果N是偶数，则将其变为N/2。

        看似普通的游戏规则，却引发了数学界的轰动。不仅学生们疯狂地玩弄这个游戏，连教师、研究员和数学大拿们也纷纷加入进来。他们发现，无论初始数字是多少，最终都会陷入自然数序列4-2-1的循环中。

        这个现象被称为冰雹猜想或角谷猜想，因为无论数字如何变化，最终都会像冰雹一样坠入这个循环谷底。这个简单的数学游戏如同一个数学黑洞，牢牢吸引着所有的自然数。

        人们将冰雹猜想的路径比喻成一棵参天大树。树根是由数字4、2和1组成的循环枝，而树枝和叶子则构成了一个奥妙的通路，覆盖了所有的自然数。这个问题看似简单，却至今没有任何数学手段和超级计算机能够证明它。冰雹猜想的魅力在于其不可预测性。数字N的转化过程变幻莫测，有些平缓温和，有些剧烈沉浮。无论初始值存在多大的误差，最后都会自行修复，直到坠入循环谷底。

        冰雹猜想与著名的蝴蝶效应截然相反。蝴蝶效应认为初始值的微小变化可能会导致结果的巨大不同，而冰雹猜想则说明无论初始值如何，最终都会收敛到相同的循环序列。

        接下来跟我一起使用所学习的C语言知识，编程实现冰雹猜想的算法，体验这个神奇猜想吧。

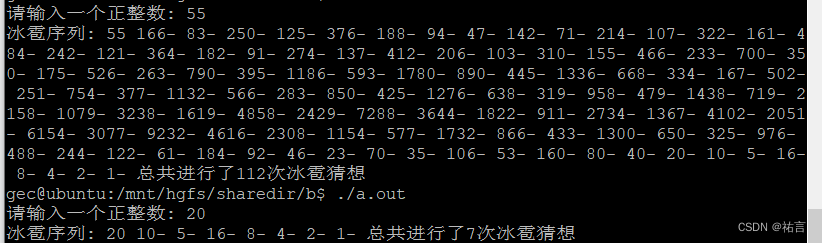
         那么究竟是如何的代码才可以实现这样的一个数学游戏呢，接下来跟我一起学习一下：

#include <stdio.h>

void hailstone(int n) {
	int cnt = 0;
    printf("%d ", n);  // 打印当前数字

    while (n != 1) {
        if (n % 2 == 0) {
            n = n / 2;  // 偶数情况
        } else {
            n = 3 * n + 1;  // 奇数情况
        }
        printf("%d- ", n);  // 打印变换后的数字
		cnt++;
    }
	printf("总共进行了%d次冰雹猜想\n", cnt);
}

int main() {
    
	int n;
    printf("请输入一个正整数: ");
    scanf("%d", &n);

    printf("冰雹序列: ");
    hailstone(n);
	
    return 0;
}

        不难看出这段代码实现了冰雹猜想的算法，它根据用户输入的正整数，计算并打印出该数字的冰雹序列。程序通过迭代的方式，根据数字的奇偶性进行变换，直到最终收敛到4-2-1的循环序列。代码还统计了进行冰雹猜想的总次数，并在最后输出。

        通过运行这段代码，可以亲自体验冰雹猜想的神奇之处，体验编程中的数学，让学习编程不是那么枯燥乏味！

今天的分享就到这里啦~