二叉树的最大深度

先来看题目描述

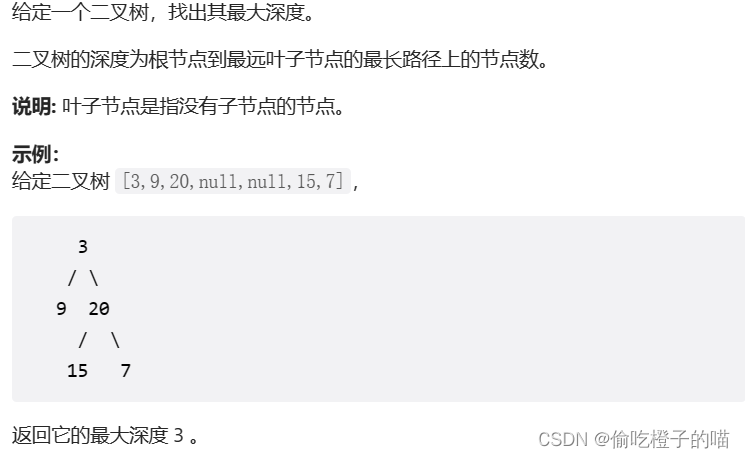
思路分析

题目想让我们求一颗二叉树的最大深度，我们就分别从左子树和右子树往下找，并每次都返回左子树和右子树中的较大值。因为父节点也算一层，所以还要在算出的最大值的基础上再加1.

代码实现

代码如下

int maxDepth(struct TreeNode* root){
    if(root==NULL)
    return 0;
    return fmax(maxDepth(root->left),maxDepth(root->right))+1;

}

相同的树

题目如下

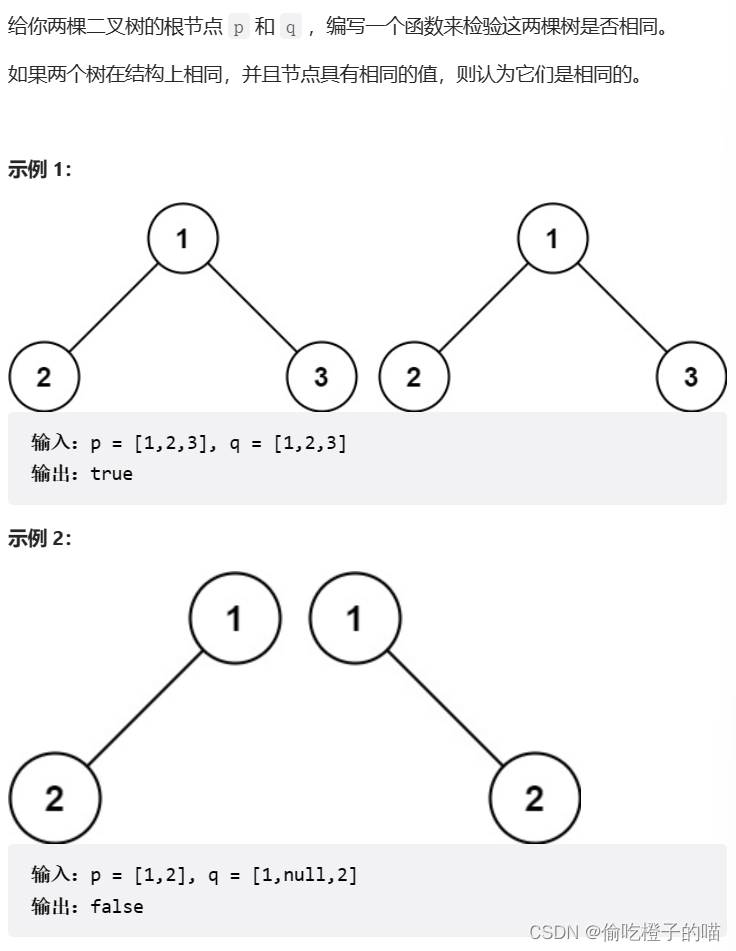
思路分析

大致思路就是左子树和左子树比较，右子树和右子树比较，如果都为空，说明走完了，则返回true。只要两个不相等或一个为空一个不为空（要单独拿出来，防止访问空指针），就返回false。

代码实现

代码如下

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p!=NULL&&q==NULL)
    return false;
    if(p==NULL&&q!=NULL)
    return false;
    if(p==NULL&&q==NULL)
    return true;
    if(p->val!=q->val)
    return false;

    return isSameTree(p->left,q->left)
    &&     isSameTree(p->right,q->right);
}

单值二叉树

题目如下

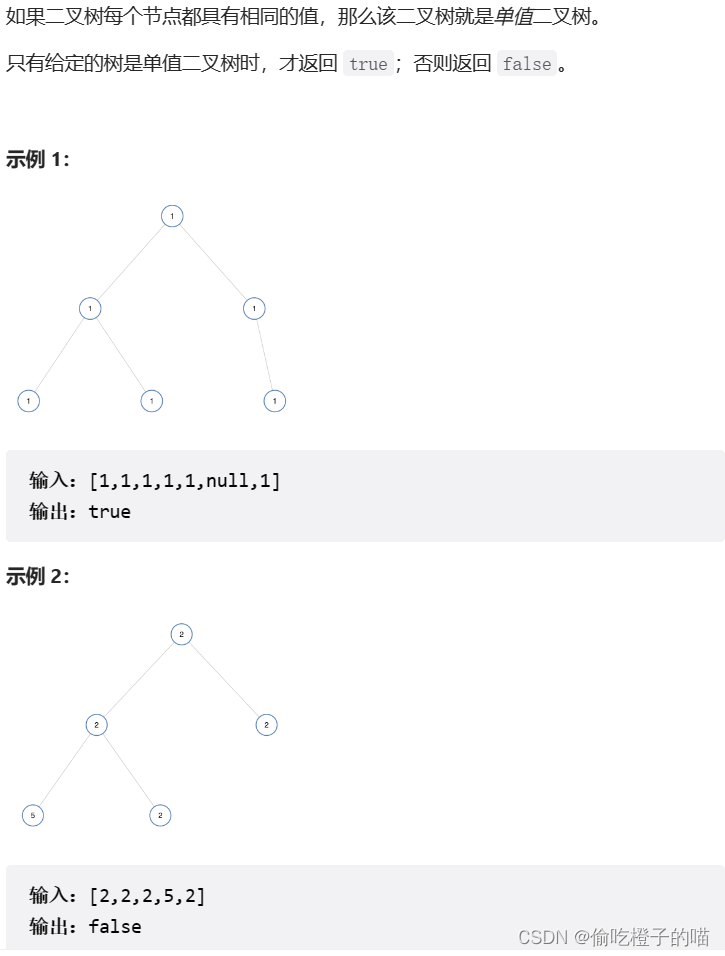
思路分析

这道题我们惯性思维可能都会先想到左右孩子相比较看是否相等，但这样其与父节点的关系就切断了，我们还要保证其与父节点也相等才对。所以正确思路是每次比较左孩子与父节点，右孩子与父节点是否相等。（注意先判断有没有左右孩子，以防访问空指针）。

代码实现

代码如下

bool isUnivalTree(struct TreeNode* root){
    if(root==NULL)
    return true;


    if(root->left!=NULL&&root->left->val!=root->val)
    {
        return false;
    }
    if(root->right!=NULL&&root->right->val!=root->val)
    {
        return false;
    }
    return isUnivalTree(root->left)
    &&     isUnivalTree(root->right);

}

二叉树的前序遍历

先来看题目描述（注意答案是放在一个数组中的）

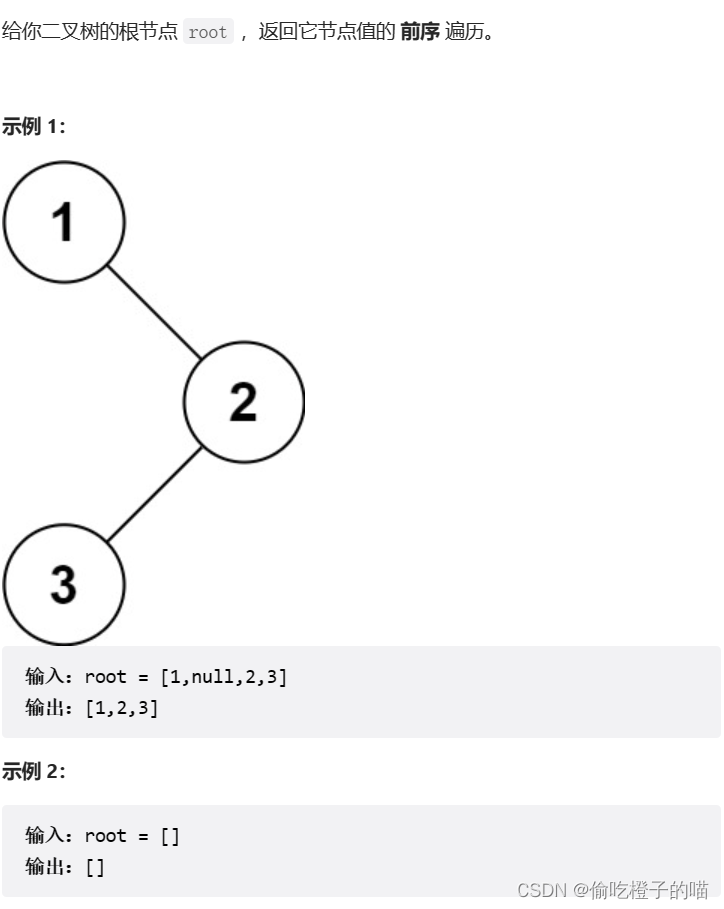
思路分析

这道题的重点在于我们要有返回值，而返回值就是数组长度，即二叉树的节点个数，难点在于要将节点的值放入一个动态开辟的数组当中去，这里访问数组下标就有别于普通访问了，求节点个数没有什么难度，这里就不细讲了，我们把代码主要分为三个主体：计算大小的函数，开辟数组并返回的主函数和将节点的值放入数组的函数，因为我们要对数组在另一个函数里访问，所以在访问下标是要传下标的地址，

代码实现

代码实现如下

int TreeSize(struct TreeNode* root)
{
    if(root==NULL)
    return 0;

    return TreeSize(root->left)+TreeSize(root->right)+1;
}

void _preorder(struct TreeNode* root,int* p,int* pi)
{
    if(root==NULL)
    return NULL;

    p[(*pi)++]=root->val;
    _preorder(root->left,p,pi);
    _preorder(root->right,p,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize=TreeSize(root);
    int* p=(int*)malloc(sizeof(int)*(*returnSize));
    
    int i=0;
    _preorder(root,p,&i);
    return p;
}

翻转二叉树

先来看题目描述

思路分析

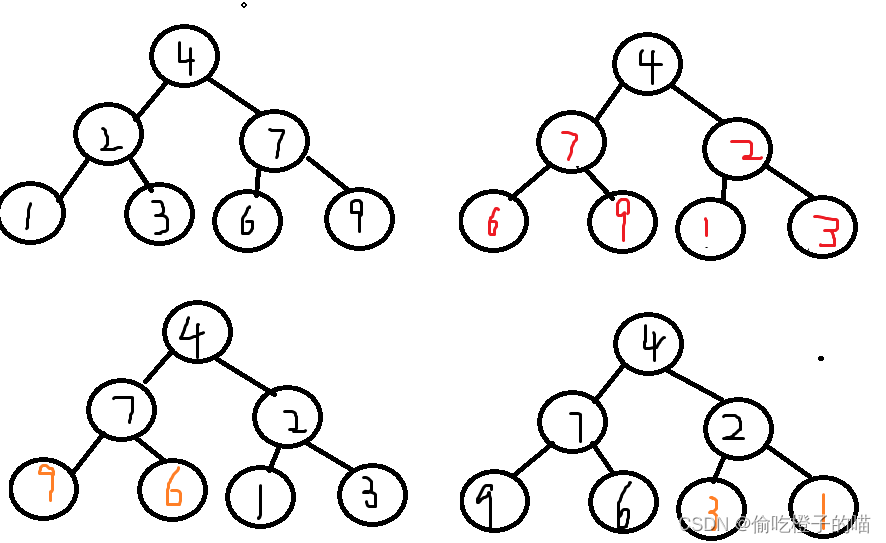
大致思路就是先交换左右孩子，然后递归左子树，然后右子树，这样就能实现翻转二叉树了，图解如上。

代码实现

代码实现如下

struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL)
    return NULL;

    struct TreeNode* temp=root->left;
    root->left=root->right;
    root->right=temp;

    invertTree(root->left);
    invertTree(root->right);
    return root;

}

对称二叉树

先来看题目描述

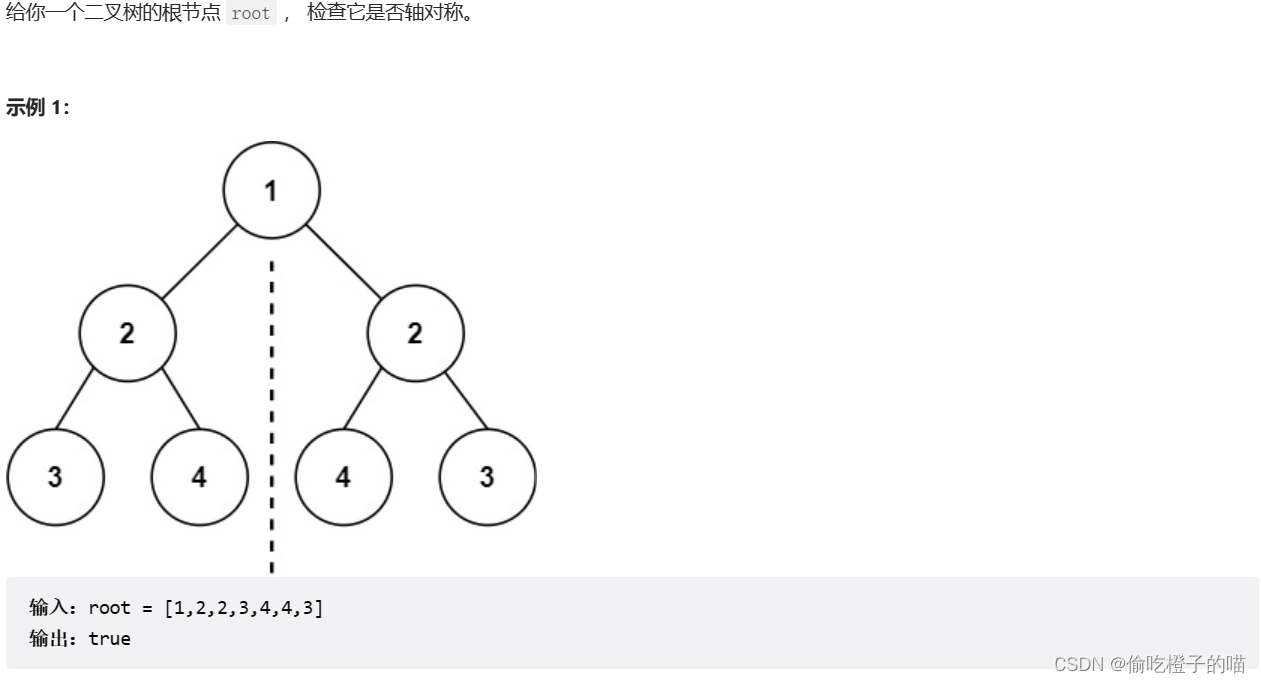
思路分析

因为我们要探究的是是否为轴对称，所以我们首先第一步要将其分成左右两个子树，后续的递归操作我们再在另一个函数中去实现，注意比较对象是左子树的左孩子，右子树的右孩子还有判断条件。

代码实现

代码实现如下

 bool _isSymmetric(struct TreeNode* leftroot,struct TreeNode* rightroot)
 {
     if(leftroot==NULL&&rightroot==NULL)
     return true;
     if(leftroot==NULL&&rightroot!=NULL)
     return false;
     if(leftroot!=NULL&&rightroot==NULL)
     return false;
     if(leftroot->val!=rightroot->val)
     return false;

     return _isSymmetric(leftroot->left,rightroot->right)
     &&     _isSymmetric(leftroot->right,rightroot->left);


 }
bool isSymmetric(struct TreeNode* root){
    if(root==NULL)
    return true;

    struct TreeNode* leftroot=root->left;
    struct TreeNode* rightroot=root->right;
    return _isSymmetric(leftroot,rightroot);

}

另一棵树的子树

题目描述如下

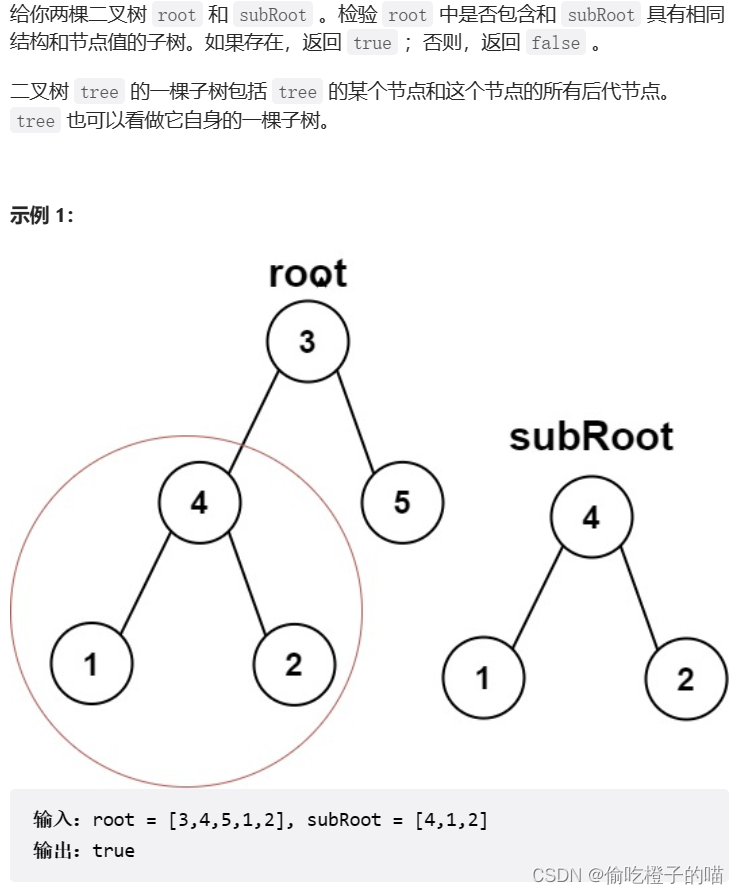
思路分析

这道题的主体思路是遍历root的所有节点，并每次与subroot进行匹配，这个操作在另一个函数中实现，逐个比较subroot和当前作为根节点的root.除了要注意比较函数中的中止递归的条件，还要注意主函数中，如果root为空了，说明遍历完了还没有找到匹配的子树，则返回false。

代码实现

代码如下

bool compare(struct TreeNode* root, struct TreeNode* subRoot){
    if(root==NULL && subRoot==NULL){
        return true;
    }
    if(root==NULL||subRoot==NULL){
        return false;
    }
    if(root->val!=subRoot->val){
        return false;
    }
        return compare(root->left,subRoot->left)&& compare(root->right,subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root==NULL){
        return false;
    }
    return compare(root,subRoot)||isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}