一、LSTM反向传播介绍
LSTM的反向传播过程相对复杂,主要因为其对应的控制门较多,而对于每一个控制门我们都需要求导,所以工作量较大。
首先我们根据LSTM结构图分析一下每个控制门的求导过程。在讲解反向传播之前,先了解一些要用到的参数意义。
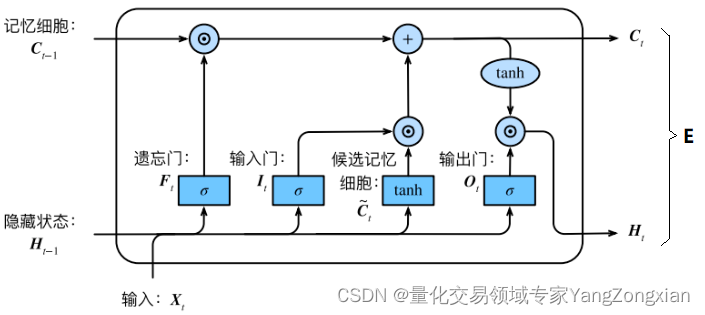
一般来说LSTM在层后会接一个全连接层FNN,全连接层后面再接一个损失函数Loss,所以这里我将全连接层反向传回给LSTM层的总误差称之为。
从上图LSTM的结构可以观察出,回传的总误差其实会由两个分支进入LSTM内部,分别是
和
。因此从宏观上看,每个LSTM单元误差传播的起始点为
和
,终点为
和
,在起始点和终点之间分别夹杂着4个控制门
,上述的这些元素,其实就是LSTM整个反向传播求导过程要涉及的全部内容。
下面我们详细介绍每个元素在求导中的处理方法。
二、反向传播过程符号定义和说明
2.1.符号意义说明
LSTM单元中误差反向传播的过程大体分为两种情况:一种是反向传播的误差来源只包含一条链,比如控制门
;另一种是反向传播的误差来源包含
和
两条传播链,比如控制门
以及
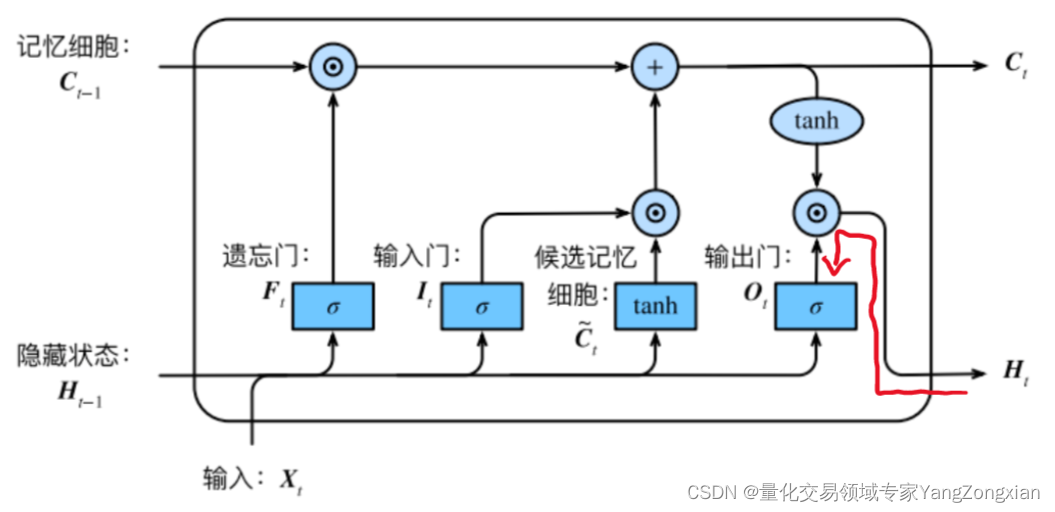
。如下图所示的遗忘门
,其反向传播的误差就是来自于红色和绿色两条传播链,计算时两条链都要计算。
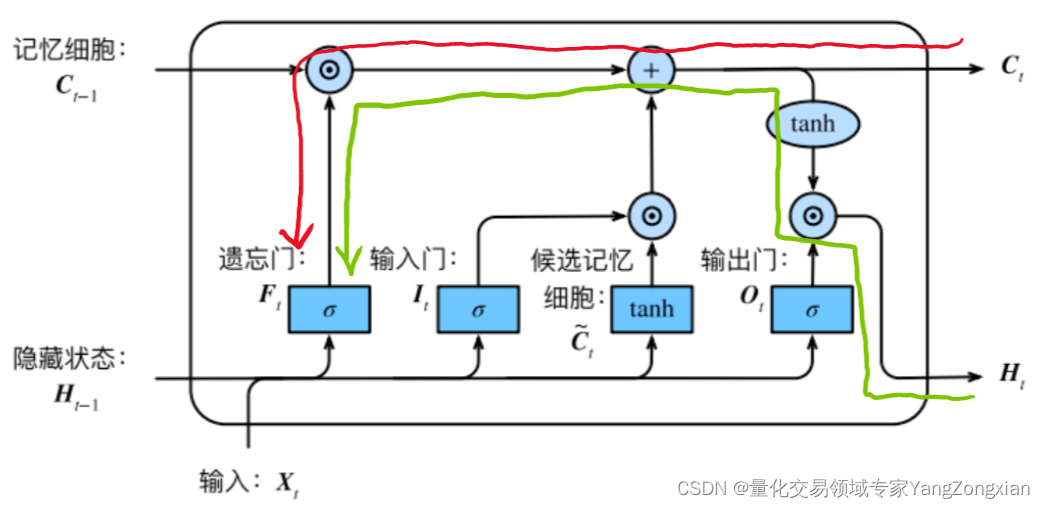
下面我们分别列举各个元素的反向传播路径:
的误差来自于
和
两条传播链,传播路径为:
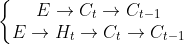
的误差来自于四条传播链,分别对应下面
四个控制门:
(1)控制门
的误差由
传来,传播路径为:
(2)控制门
的误差由
和
传来,传播路径为:
(3)控制门
的误差由
和
传来,传播路径为:
(4)控制门
的误差由
和
传来,传播路径为:
列举一下每个元素求偏导过程中的符号定义
- LSTM单元反向传播的起点
和
的误差,是由上一层传递来的,这里表示为
和
,是已知常量。
- LSTM单元中的
是由
和
计算而来,所以求导过程中存在
到
的偏导数
,以及
到
的偏导数
。
分别由
计算而来,所以求导过程中存在
分别到
的偏导数
,
,
。
- LSTM单元中从控制门
到
存在偏导数
,
,
,
。从
和
到
的偏导数则为
和
。
- 最后在求偏导的过程中还会用到一些前向传播的数值,如
,
,
,
等,这些参数在计算前向传播过程中都可以加以保留。
- 在理清上述这些反向传播中存在的关系后,下面我们就可以完成整个LSTM单元的反向传播计算了。
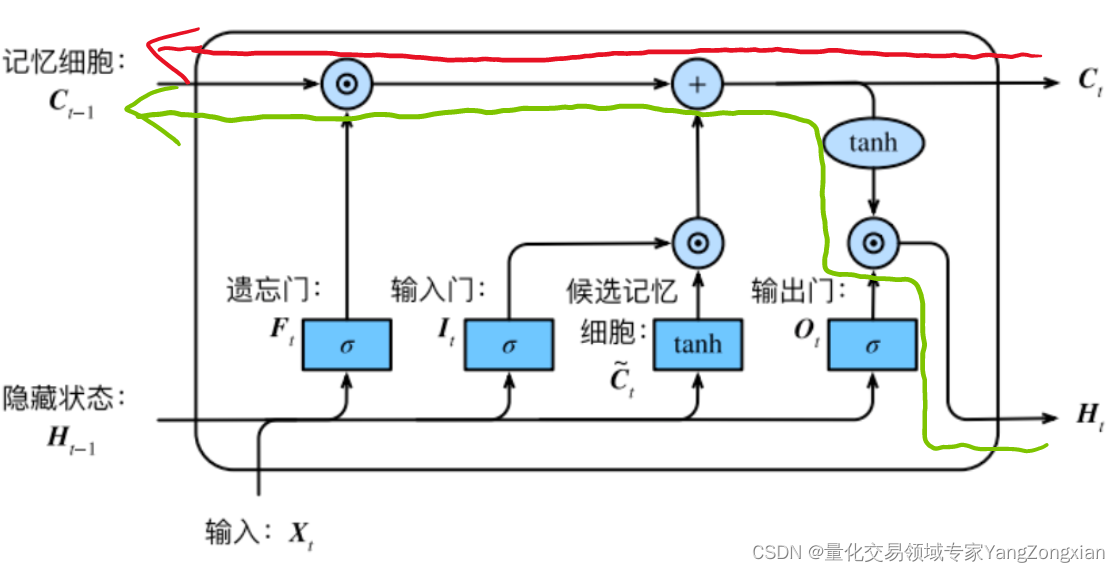
LSTM计算顺序如下图所示:
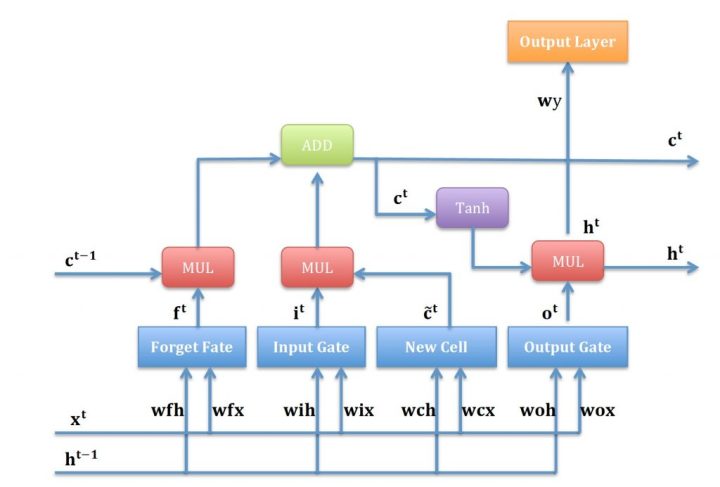
介绍完这些符号定义后,下面就可以开始LSTM的反向传播计算了。
2.2.重要细节——特殊的传播链Ct
是一条比较特殊的传播链,在前向传播时,每个sample都中包含n个Timestep,在第一个Timestep计算时,
的初始值是零矩阵,在后续的Timestep计算时
会进行不断累计和向后传递。在当前LSTM层计算完成后,向下个LSTM层传递时,只向后传递输出的状态
,作为下个LSTM层的输入Xh,而当前层的
值不再向下个LSTM层传递。
所以同理,在反向传播时,下一层的会反向传播到上一层作为误差输入,但
不会回传,所以每一层LSTM按照时间步倒序计算反向传播过程中,计算第一个Timestep时
的初始值也是零矩阵,并且在后续时间步中进行累计和传递。
这一规则十分重要,在这里单独强调,后续内容不再重复说明。
三、LSTM反向传播流程解析
上一节我们说过,从反向传播链终点的角度出发,有两种类型的传播链,即 链和
链 。而细分
的传播链其实又有两种类型,即包含
的和不包含
的。所以反向传播链大体上可分为三类,下面来讲解这三种流程。
3.1.第一类偏导: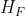 ,
,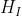 ,
,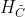

3.1.1.遗忘门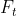 求导过程
求导过程
两条完整求导路径表达式如下
3.1.1.1.绿色路径到
的偏导
3.1.1.2.红色路径到
的偏导
3.1.1.3.遗忘门到
的偏导
3.1.1.4.两条路径表达式合并
3.1.2.输入门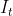 求导过程
求导过程
原理同上,这里直接写
3.1.2.1.到
的偏导
3.1.2.2.到
的偏导
3.1.2.3.输入门到
的偏导
3.1.2.4.两条路径表达式合并
3.1.3.候选记忆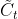 求导过程
求导过程
原理同上,这里直接写
3.1.3.1.到
的偏导
3.1.3.2.到
的偏导
3.1.3.3.候选记忆到
的偏导
3.1.3.4.两条路径表达式合并
3.2.第二类偏导: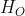
完成表达式如下
3.2.1.红色路径到
偏导
3.2.2.到
偏导
3.2.3.表达式合并
3.3.第三类偏导: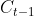
两条完整求导路径表达式如下
3.3.1.红色路径到
的偏导
3.3.2.绿色路径到
的偏导
3.3.3.两条路径表达式合并
3.4.合并
四个控制门计算完成后,最终合并起来,表达式如下:
四、权重的反向传播
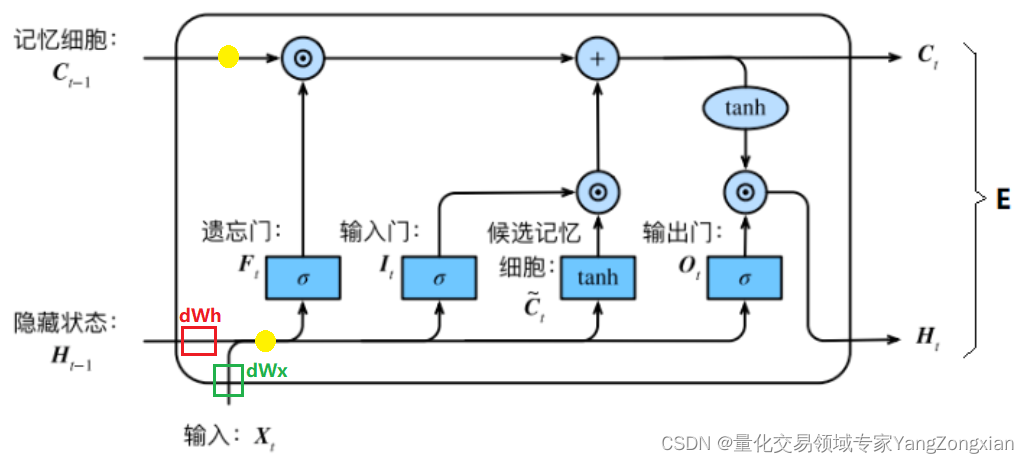
在上述第三节的求导过程结束后,此时误差就传递到了上图中的两个黄色圆圈部分,显然还差一步反向传播就完成了。最后一步就是将误差从黄色的圆圈部分分别传递到,
,
。对于
和
来说,要计算两个权重矩阵
和
,而对于
来说,不必求矩阵,直接向后传递即可。
在前向传播时计算流程如下:
由上式可得,反向传播的表达式可以表达如下:
最后还剩一个偏置项,我们将上一节得出的
直接降维即可得到
,具体的程序实现方法会在下一篇文章中更直观的介绍。
五、总结
上面就是一个完整的LSTM单元反向传播流程,至此本文已经对LSTM的反向传播理论基础进行了比较清楚的讲解。结合上一篇LSTM网络前向传播原理讲解,相信大家对LSTM的基本原理有了一个比较清晰的认识了。
但这仅仅是单一的LSTM模型前向传播和反向传播原理,不足以构成一个完整的模型。但是有了上述基础,下篇文章中我们就可以1:1实现一个包含输入,隐藏层,输出,损失函数的完整的神经网络模型了。
文章正在写作中……
参考文献:
循环神经网络RNN&LSTM推导及实现 - 知乎
LSTM的推导与实现 - liujshi - 博客园











![[附源码]JAVA毕业设计微博网站(系统+LW)](https://img-blog.csdnimg.cn/9ab152d6f2344451b071fb45539fa62a.png)
