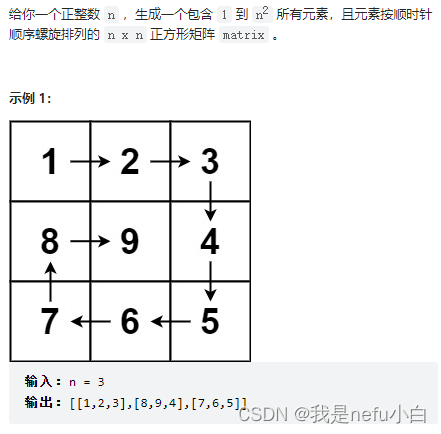
最近周赛有两个差不多的题目,都是关于图的,之前也没有怎么练过关于图的题目,来记录一下。
T1
力扣T320周赛:T3:到达首都的最少油耗
class Solution {
//结果
long result ;
public long minimumFuelCost(int[][] roads, int seats) {
//存储和每个节点有连接的节点
Map<Integer,List<Integer>> map = new HashMap<>();
for(int[] road : roads){
map.computeIfAbsent(road[0],t -> new ArrayList<>()).add(road[1]);
map.computeIfAbsent(road[1],t -> new ArrayList<>()).add(road[0]);
}
//找路径
for(int i : map.getOrDefault(0,new ArrayList<>())){
//从from=0开始找,找到所有与0连接的路,i为其中一个和0直接连接的路的开始
minimumFuelCost(i,0,map,seats);
}
return result;
}
int minimumFuelCost(int n ,int from ,Map<Integer,List<Integer>> map,int seats){
//不论到哪,油耗为1
int count = 1;
for(int i : map.get(n)){
//如果当前节点和出发节点一致,那么油耗为0,否则根据该节点继续往下找,直到找到这条路结束
count += i == from ? 0 : minimumFuelCost(i,n,map,seats);
}
result += (count + seats -1)/seats;
return count;
}
}
该题解的思路主要是:先将每个节点和他连接的记录起来,我们拿其中一个示例来说:
示例2:
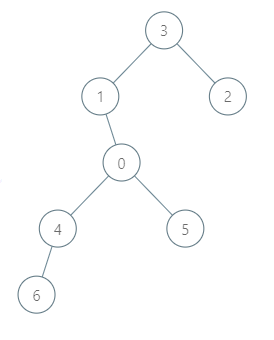
输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出:7
解释:
- 代表 2 到达城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 5 直接到达首都,消耗 1 升汽油。
- 代表 6 到达城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。
最少消耗 7 升汽油。。
经过map记录之后的结果为:
节点 -> 连接的其他节点
k=0,v=[1, 4, 5]
k=1,v=[3, 0]
k=2,v=[3]
k=3,v=[1, 2]
k=4,v=[0, 6]
k=5,v=[0]
k=6,v=[4]
我们对from=0的节点开始遍历,然后找到1,接着找到与1连接的3,然后找到与3连接的2,计算路经需要油耗,其他的类推,大致上整体是这么个过程。
但是我们不难发现,我们把座位拿掉之后,实际上就是找与该节点连接的子树的路径长,但是有座位限制,实际上就是几个节点一起出发一起去下一站,一起之后看做一个节点耗费一份油。
T2
OK这个题目看完了,我们再看一个类似的题目:
力扣T320周赛:T3:两个城市间路径的最小分数
这个题和上一提非常相似,但是没又上一题那么复杂,我们直接看代码
public int minScore(int n, int[][] roads) {
HashMap<Integer, List<int[]>> map = new HashMap<>();
for (int[] road : roads) {
map.computeIfAbsent(road[0], t -> new ArrayList<>()).add(new int[] { road[1], road[2] });
map.computeIfAbsent(road[1], t -> new ArrayList<>()).add(new int[] { road[0], road[2] });
}
return minScore(1, map);
}
private int minScore(int n, HashMap<Integer, List<int[]>> map) {
int min = Integer.MAX_VALUE;
for (int[] next : map.replace(n, List.of())) {
min = Math.min(min, Math.min(next[1], minScore(next[0], map)));
}
return min;
}
}
这个题不多解释,跟上个题目类似。
总结
关于图的题目,基本上的思路就是,首先构造图的相连关系,给的数组表达的不清楚,我们需要清楚的知道,和a相连的都有谁,和b相连的都有谁…等待,如果有路径长度就在后面跟路径长度。
所以步骤就是:
- 先确定连通图
//int[][] roads
//构造连通图,如果有路径key就用就用List<int[]>,int[0]为长连通状况,int[1]为路径长
Map<Integer,List<Integer>> map = new HashMap<>();
for(int[] road : roads){
map.computeIfAbsent(road[0],t -> new ArrayList<>()).add(road[1]);
map.computeIfAbsent(road[1],t -> new ArrayList<>()).add(road[0]);
}
当连通之后,我们需要知道是从哪走,要到哪去,递归肯定避免不了的,关键是怎么递归。
- 确定开始路线
- T1
public long minimumFuelCost(int[][] roads, int seats) {
....
//第一题,题目要求都要到达0,所以就以0为起点找路径
for(int i : map.getOrDefault(0,new ArrayList<>())){
//从from=0开始找,找到所有与0连接的路,i为其中一个和0直接连接的路的开始
minimumFuelCost(i,0,map,seats);
}
return result;
}
int minimumFuelCost(int n ,int from ,Map<Integer,List<Integer>> map,int seats){
........
}
- T2:
public int minScore(int n, int[][] roads) {
........
//都要从1开始,找到最后一个节点,开头和结尾是固定,为了方便我们选择从头开始
return minScore(1, map);
}
private int minScore(int n, HashMap<Integer, List<int[]>> map) {
........
}
我们根据题意确定不同的起点,然后再根据题意往下继续找,就可以得到我们需要的解了。




![[附源码]JAVA毕业设计微博网站(系统+LW)](https://img-blog.csdnimg.cn/9ab152d6f2344451b071fb45539fa62a.png)