摘要

剑指 Offer 53 - II. 0～n-1中缺失的数字

一、二分法

1.1 二分法分析

排序数组中的搜索问题，首先想到 二分法 解决。
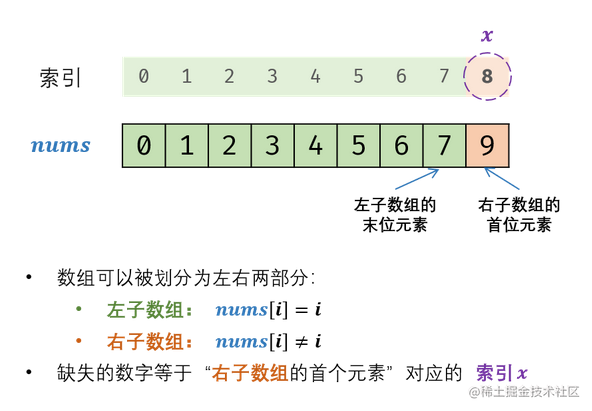
根据题意，数组可以按照以下规则划分为两部分。

• 左子数组： nums[i]=i；
• 右子数组： nums[i]≠i；

缺失的数字等于 “右子数组的首位元素” 对应的索引；因此考虑使用二分法查找 “右子数组的首位元素”。

算法解析：

• 初始化： 左边界 i=0i=0 ，右边界 j=len(nums)−1j=len(nums)−1 ；代表闭区间 [i,j]。
• 循环二分： 当 i≤ji≤j 时循环 （即当闭区间 [i,j] 为空时跳出） ；
  • 计算中点 m=(i+j)>> 1，其中 为向下取整除法；
  • 若 nums[m]=m ，则 “右子数组的首位元素” 一定在闭区间 [m+1,j] 中，因此执行 i=m+1；
  • 若 nums[m]≠m ，则 “左子数组的末位元素” 一定在闭区间 [i,m−1] 中，因此执行 j=m−1j=m−1；
• 返回值：跳出时，变量i和j分别指向 “右子数组的首位元素” 和 “左子数组的末位元素” 。因此返回 i 即可。

1.2 复杂度分析

• 时间复杂度 O(logN)： 二分法为对数级别复杂度。
• 空间复杂度 O(1)：几个变量使用常数大小的额外空间。

1.3 code 示例

public int missingNumber(int[] nums) {
    int i = 0;
    int j = nums.length - 1;
    while (i <= j) {
        int m = (i + j) >> 1;
        if (nums[m] == m) {
            i = m + 1;
        } else {
            j = m - 1;
        }
    }
    return i;
}

二、其他方法

2.1 哈希集合分析

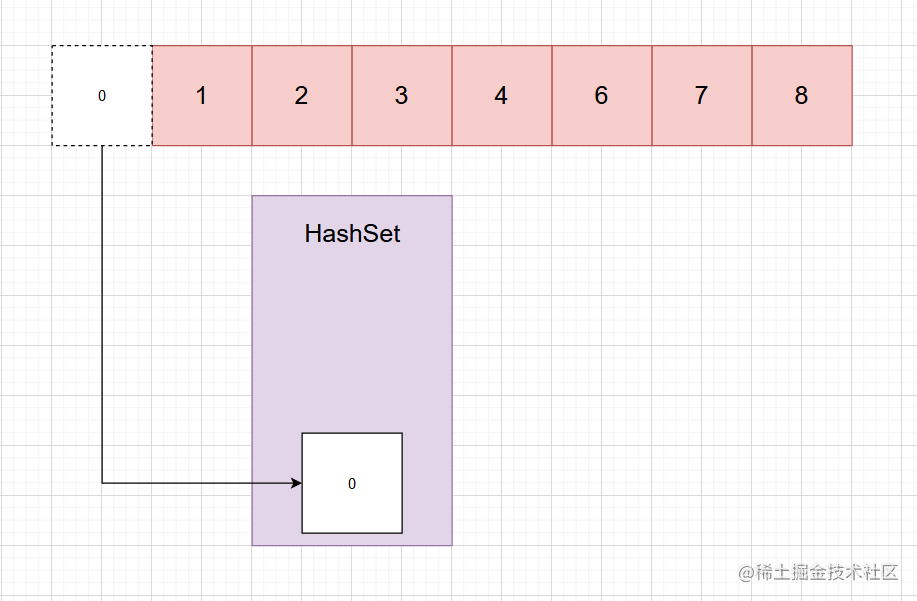
最直观的方法是使用哈希集合。

首先遍历数组 nums，将数组中的每个元素加入哈希集合，然后依次检查从 0到 n−1的每个整数是否在哈希集合中，不在哈希集合中的数字即为缺失的数字。由于哈希集合的每次添加元素和查找元素的时间复杂度都是 O(1)，因此总时间复杂度是 O(n)。

2.2 复杂度分析

• 时间复杂度：O(n)，其中 n是数组 nums的长度加 1。遍历数组 nums 将元素加入哈希集合的时间复杂度是 O(n)，遍历从 0 到 n−1 的每个整数并判断是否在哈希集合中的时间复杂度也是 O(n)。

• 空间复杂度：O(n)，其中 n 是数组 nums的长度加 1。哈希集合中需要存储 n−1个整数

2.3 code 示例

class Solution {
    public int missingNumber(int[] nums) {
        Set<Integer> set = new HashSet<Integer>();
        int n = nums.length + 1;
        for (int i = 0; i < n - 1; i++) {
            set.add(nums[i]);
        }
        int missing = -1;
        for (int i = 0; i <= n - 1; i++) {
            if (!set.contains(i)) {
                missing = i;
                break;
            }
        }
        return missing;
    }
}

使用直接遍历方式来查找缺失的数字。

class Solution {
    public int missingNumber(int[] nums) {
        int n = nums.length + 1;
        for (int i = 0; i < n - 1; i++) {
            if (nums[i] != i) {
                return i;
            }
        }
        return n - 1;
    }
}

博文参考