题目
考虑被控对象
G
(
s
)
=
3
s
+
4
s
4
+
5
s
3
+
10
s
2
+
6
s
+
4
G(s)=\frac{3 s+4}{s^{4}+5 s^{3}+10 s^{2}+6 s+4}
G(s)=s4+5s3+10s2+6s+43s+4
和特征模型
y
(
k
)
=
ϕ
T
(
k
−
1
)
θ
(
k
)
y(k)=\boldsymbol{\phi}^{\mathrm{T}}(k-1)\boldsymbol{\theta}(k)
y(k)=ϕT(k−1)θ(k)
其中
ϕ
(
k
−
1
)
=
[
y
(
k
−
1
)
y
(
k
−
2
)
u
(
k
−
1
)
]
T
θ
(
k
)
=
[
f
1
(
k
)
f
2
(
k
)
g
0
(
k
)
]
T
\begin{aligned} \phi(k-1) =& [\begin{matrix} y(k-1) & y(k-2) & u(k-1) \end{matrix}]^{\mathrm{T}} \\ \theta(k) =& [\begin{matrix} f_{1}(k) & f_{2}(k) & g_{0}(k) \end{matrix}]^{\mathrm{T}} \end{aligned}
ϕ(k−1)=θ(k)=[y(k−1)y(k−2)u(k−1)]T[f1(k)f2(k)g0(k)]T
控制输入
u
u
u 取如下四种形式:
- 阶跃信号 u ( k ) = 10 u(k)=10 u(k)=10;
- 经 “平滑” 的阶跃信号 u ( k ) = 0.97 u ( k − 1 ) + 0.3 u(k)=0.97u(k-1)+0.3 u(k)=0.97u(k−1)+0.3;
- 周期为 1 1 1 的正弦信号 u ( k ) = 10 cos ( 2 π k T ) u(k)=10\cos(2\pi kT) u(k)=10cos(2πkT);
- 周期为 1 1 1 的方波信号 u ( k ) = 10 sign ( cos ( 2 π k T ) ) u(k)=10\operatorname{sign}(\cos(2\pi kT)) u(k)=10sign(cos(2πkT))。
采样周期取 Δ t = 0.05 \Delta t=0.05 Δt=0.05。
仿真
下面的所有仿真都使用 simucpp。
原系统阶跃响应结果
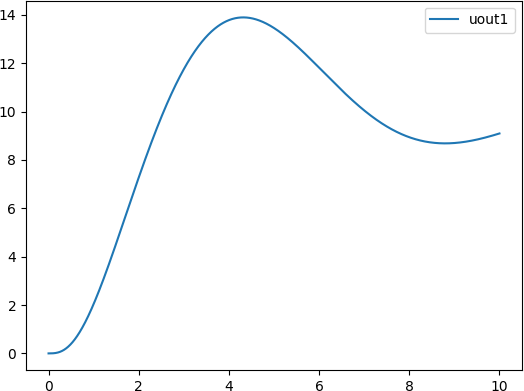
原系统阶跃响应程序
# include "simucpp.hpp"
using namespace simucpp;
using namespace zhnmat;
using namespace std;
int main() {
Simulator sim1;
FUInput(uin1, &sim1);
FUOutput(uout1, &sim1);
auto *tf1 = new TransferFcn(&sim1, vecdble{3, 4}, vecdble{1, 5, 10, 6, 4});
sim1.connectU(uin1, tf1, 0);
sim1.connectU(tf1, 0, uout1);
uin1->Set_Function([](double t){return 10;});
sim1.Initialize();
sim1.Simulate(10);
sim1.Plot();
return 0;
}
- 阶跃信号
u
(
k
)
=
10
u(k)=10
u(k)=10
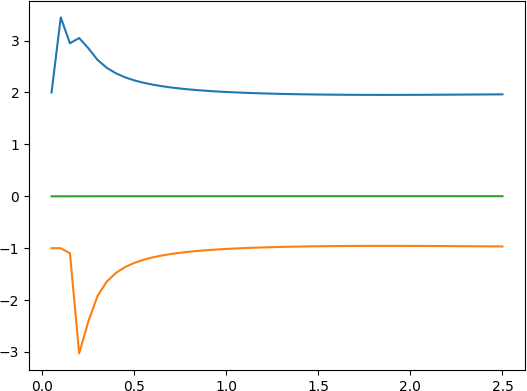
- 经 “平滑” 的阶跃信号
u
(
k
)
=
0.97
u
(
k
−
1
)
+
0.3
u(k)=0.97u(k-1)+0.3
u(k)=0.97u(k−1)+0.3
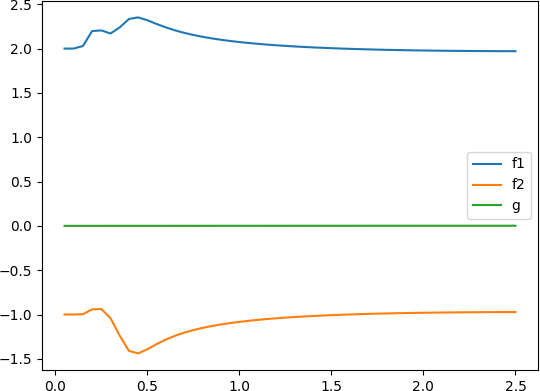
- 周期为
1
1
1 的正弦信号
u
(
k
)
=
10
cos
(
2
π
k
T
)
u(k)=10\cos(2\pi kT)
u(k)=10cos(2πkT)
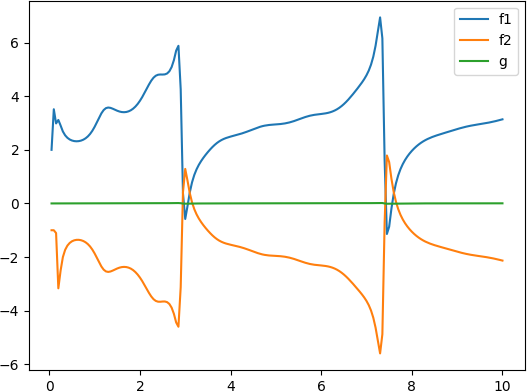
- 周期为
1
1
1 的方波信号
u
(
k
)
=
10
sign
(
cos
(
2
π
k
T
)
)
u(k)=10\operatorname{sign}(\cos(2\pi kT))
u(k)=10sign(cos(2πkT))
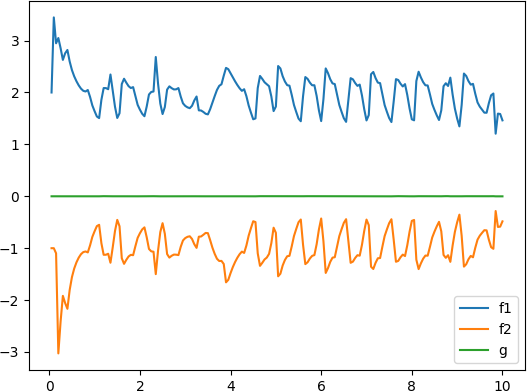
全部代码
/**************************************************************
特征模型仿真例1:参数辨识
simucpp版本:2.1.12
**************************************************************/
#include <cmath>
#include "simucpp.hpp"
#include "matplotlibcpp.h"
namespace plt = matplotlibcpp;
using namespace simucpp;
using namespace zhnmat;
using namespace std;
constexpr double LIMIT(double x, double min, double max) {
return x<=min ? min : (x>=max ? max : x);}
constexpr double SIGN(double x) {
return x<0 ? -1 : (x>0 ? 1 : 0);}
class ParamIdentifier {
public:
ParamIdentifier(double sigma=0) {
_P = eye(3) * 1e6;
_theta = Mat(vecdble{2, -1, 0});
_lambda = 0.5;
};
Mat Update(double u, double y) {
Mat x(vecdble{_yk1, _yk2, u});
Mat K = 1/(_lambda + (x.T()*_P*x).at(0, 0)) * _P * x;
_P = (eye(3) - K*x.T()) * _P / _lambda;
_theta += K * (y - (x.T()*_theta).at(0, 0));
_yk2 = _yk1; _yk1 = y;
return _theta;
}
Mat _P; // P矩阵
Mat _theta; // 特征模型参数(f1, f2, g)
double _lambda; // 遗忘因子
double _yk1=0, _yk2=0; // y(k-1)
};
int main() {
Simulator sim1;
FUConstant(uin1, &sim1);
FUOutput(uout1, &sim1);
auto *tf1 = new TransferFcn(&sim1, vecdble{3, 4}, vecdble{1, 5, 10, 6, 4});
ParamIdentifier idf;
sim1.connectU(uin1, tf1, 0);
sim1.connectU(tf1, 0, uout1);
sim1.Initialize();
Mat theta(3, 1);
vecdble plott, plotf1, plotf2, plotg;
double outValue = 0;
for (uint32_t i = 0; i < 50; i++) { // 周期0.05仿真50次为2.5秒
// outValue = 10;
outValue = 0.97*outValue + 0.3;
// outValue = 10*cos(0.1*i*M_PI);
// outValue = 10*SIGN(cos(0.1*i*M_PI));
uin1->Set_OutValue(outValue);
for (uint32_t j = 0; j < 50; j++) // 步长0.001秒仿真50次为T=0.05秒
sim1.Simulate_OneStep();
theta = idf.Update(uin1->Get_OutValue(), uout1->Get_OutValue());
plott.push_back(0.05*(i+1));
plotf1.push_back(theta.at(0, 0));
plotf2.push_back(theta.at(1, 0));
plotg.push_back(theta.at(2, 0));
}
plt::named_plot("f1", plott, plotf1);
plt::named_plot("f2", plott, plotf2);
plt::named_plot("g", plott, plotg);
plt::legend();
plt::show();
// sim1.Plot();
return 0;
}