Nova是INV的一种实现方案，所谓IVC是指Prover可以向Verifier证明 $z_i=F^{(i)}(z_0)$ 。

最朴素的做法是直接进行i次迭代，每次迭代都进行一次zkSnark，但这样做有三个问题：

• Prover所需内存大小为 $\Omega (i\ast \mid F\mid )$
• 生成的proof不是incrementally updatable的
• Verify时间跟$i$有关

Nova 的整体思路是将原始的 R1CS 问题转化为一种更加灵活且支持Folding形式的relaxed R1CS，并在此基础上，进一步构造了 committed relaxed R1CS，committed relaxed R1CS主要保护了witness的机密性，然后基于 committed relaxed R1CS构建了IVC方案。

Folding Scheme是Nova构造IVC的核心，通过前面R1CS和relaxed R1CS两篇博文的讲解，相信大家对如何构造一个Folding Scheme已经有了初步了解。接下来本文将介绍如何通过Folding Scheme去构造IVC，主要包括两部分：

• 简单回顾Folding Scheme
• IVC讲解

1. Folding Scheme

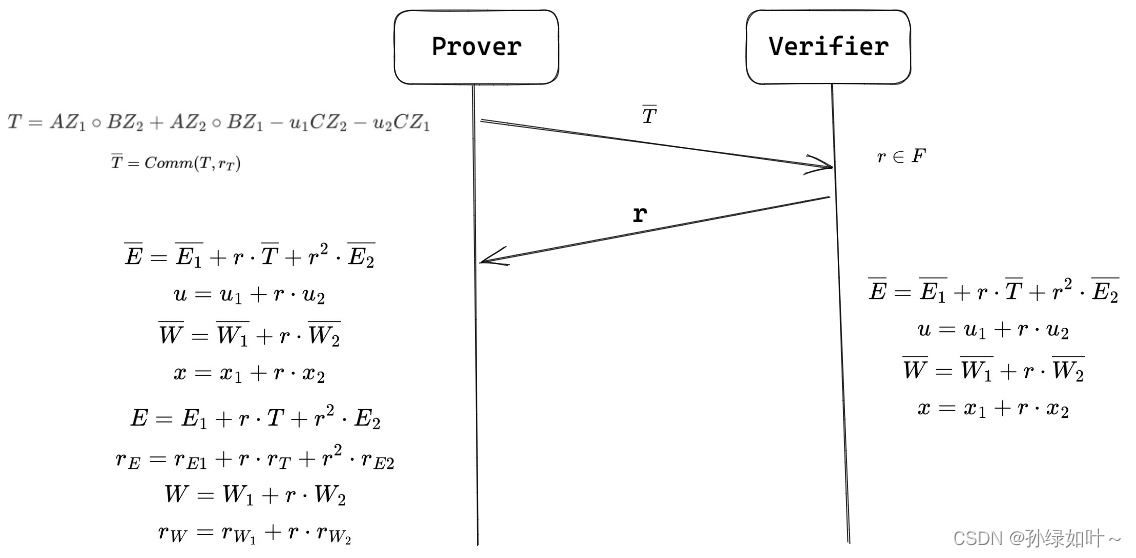
上述过程可通过Fiat-Shamir Transform变为非交互，全称是non-interactive folding scheme(NIFS).

NIFS由(G,K,P,V)四个算法构成：

2. IVC

首先通过引入augmented function F’描述一个简单的IVC过程。令$U_i、u_i$为两个committed relaxed R1CS instances，其中$U_i$代表前$i-1$次F’正确执行的输出(running)，$u_i$代表前$i$次F’正确执行的输出(incremental)。

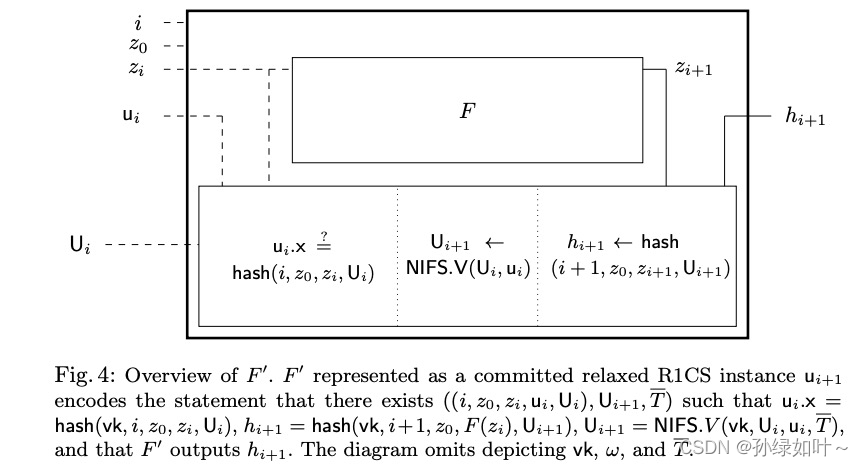
F’主要干两件事：

1. 执行incremental computation，也就是调用F输出$z_{i+1}$
2. 调用NIFS的verifier折叠输出$U_{i+1}$

需要注意的是F’并没有直接输出$U_{i+1}$,而是输出了$h_{i+1}$，因为$U_{i+1}$包含在$u_{i+1}.$x中，则在下一步折叠$u_{i+1}.$x和$U_{i+1}.$x时会卡住，因此这里以定长的哈希结果作为输出。

然后IVC Prover计算一个新的instance $u_{i+1}$,用来证明第$i+1$次F’执行的正确性，即证明了以上两点。

令$(u_{\perp },w\perp )$是一对平凡的instance-witness对，其中E、W和x是相应的令向量，$r_E=0、r_w=0$，$\overline{E}、\overline{W}$分别是E、W对应的承诺。

在第$i+1$次迭代中，IVC Prover调用F’计算$((U_{i+1},W_{i+1}),(u_{i+1},w_{i+1}))$，则相应的IVC proof ${\pi }_{i+1}=((U_{i+1},W_{i+1}),(u_{i+1},w_{i+1}))$。F’具体的定义如下：

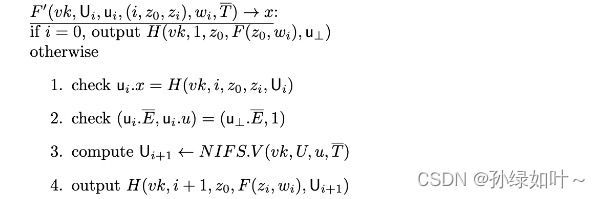
由于F’是能够在多项式时间内计算的，可以用一个committed relaxed R1CS 结构来表示F’执行：
$$(u_{i+1},w_{i+1})\leftarrow trace(F^{\prime },(v{k}_i,U_i,u_i,(i,z_0,z_i),w_i,\overline{T}))$$
现在，我们给出IVC的完整定义：

使用zkSnark压缩IVC proof

上述完整的介绍了IVC过程，但还有一个问题没解决，即Prover如何去证明一个IVC proof是有效的？

很明显Prover可以使用zkSnark来证明，但如果采用 zk­SNARK 构造证明的话，需要证明诸如向量的承诺等于特定的值等复杂问题，所以Nova使用Spartan变种来压缩Nova IVC proof，这里只介绍如何使用zkSnark去证明IVC proof是有效的，细节如下：

参考：
Nova: Recursive Zero-Knowledge Arguments from Folding Schemes