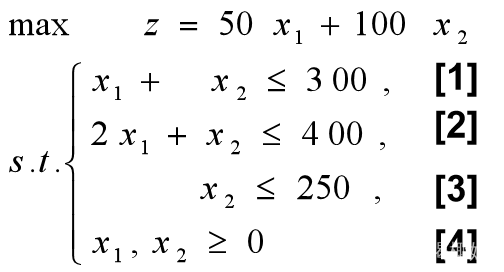一、线性规划的可行解

 若x1,x2满足条件[1]-[4],则称向量为线性规划问题的一个可行解。

 例如

 其中x(1),x(2)为可行解，而x(3),x(4)不是可行解。

二、线性规划的可行域

所有可行解构成的集合称为该线性规划的可行域。

三、线性规划的最优解

使目标函数最大或最小的可行解

四、 可行解、可行域、最优解的几何意义

可以用图解法求解两个决策变量的线性规划问题。

举例：

例1

 Q2对应的点就是线性规划问题的唯一最优解：x*=[x1*=3.5,x2*=1.5]T。

 例2 

 可以看出，Q2Q3上的点全是最优解。

即问题有无穷多最优解。

例3

 可以看出，在可行域内，当可行解变化时，目标函数可以无限增大。即问题为无界解。

 例4

 可以看出，该问题两个约束矛盾，无可行解。

综上所述，对于线性规划问题，其结果不外乎下面几种情况：

1. 有最优解：唯一最优解或无穷多最优解，且最优解一定在可行域某顶点达到；
2. 无界解；
3. 无可行解。

在实际的线性规划模型的计算中，如果遇到3情况，说明漏掉了重要的约束；如果遇到4情况，说明问题有约束冲突，检查约束条件，一般采取如下策略：要么留下主要约束，去掉与之矛盾的次要约束；要么承认矛盾的合理性，采用多目标规划。