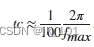数学建模常用模型（五）：多元回归模型

由于客观事物内部规律的复杂性及人们认识程度的限制，无法分析实际对象内在的因果关系，建立合乎机理规律的数学模型。所以在遇到有些无法用机理分析建立数学模型的时候，通常采取搜集大量数据的办法，基于对数据的统计分析去建立模型，其中用途最为广泛的一类随即模型就是统计回归模型。
回归模型确定的变量之间是相关关系，在大量的观察下，会表现出一定的规律性，可以借助函数关系式来表达，这种函数就称为回归函数或回归方程。
这是我自己总结的一些代码和资料（本文中的代码以及参考书籍等），放在github上供大家参考：https://github.com/HuaandQi/Mathematical-modeling.git

1.用回归模型解题的步骤

一：确定回归模型属于那种基本类型，然后通过计算得到回归方程的表达式；
①根据试验数据画出散点图；
②确定经验公式的函数类型；
③通过最小二乘法得到正规方程组；
④求解方程组，得到回归方程的表达式。

二：是对回归模型进行显著性检验。yunx
①相关系数检验，检验线性相关程度的大小；
②F检验法（这两种检验方法可以任意选）；
③残差分析；
④对于多元回归分析还要进行因素的主次排序；
如果检验结果表示此模型的显著性很差，那么应当另选回归模型了。

2.模型的转化

非线性的回归模型可以通过线性变换转变为线性的方程来进行求解;
函数关系式：可以通过线性变换：转化为一元线性方程组来求解，对于多元的也可以进行类似的转换。

3. 程序实例

3.1多元线性回归模型

一元线性回归是一个主要影响因素作为自变量来解释因变量的变化，但是在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。

import pandas as pd
import numpy as np
import statsmodels.api as sm# 实现了类似于二元中的统计模型，比如ols普通最小二乘法
import statsmodels.stats.api as sms#实现了统计工具，比如t检验、F检验...
import statsmodels.formula.api as smf
import scipy

np.random.seed(991)# 随机数种子

# np.random.normal(loc=0.0, scale=1.0, size=None)
# loc：float  此概率分布的均值（对应着整个分布的中心)，loc=0说明这一个以Y轴为对称轴的正态分布，
# scale：float 此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
# size：int or tuple of ints  输出的shape，默认为None，只输出一个值
# 数据生成
x1 = np.random.normal(0,0.4,100)# 生成符合正态分布的随机数(均值为0,标准差0.4,所生成随机数的个数为100)
x2 = np.random.normal(0,0.6,100)
x3 = np.random.normal(0,0.2,100)
eps = np.random.normal(0,0.05,100)# 生成噪声数据，保证后面模拟所生成的因变量的数据比较接近实际的环境

X = np.c_[x1,x2,x3]# 调用c_函数来生成自变量的数据的矩阵，按照列进行生成的；100×3的矩阵
beta = [0.1,0.2,0.7]# 生成模拟数据时候的系数的值
y = np.dot(X,beta) + eps# 点积+噪声(dot是表示乘)
X_model = sm.add_constant(X)# add_constant给矩阵加上一列常量1，便于估计多元线性回归模型的截距，也是便于后面进行参数估计时的计算
model = sm.OLS(y,X_model)# 调用OLS普通最小二乘法来求解
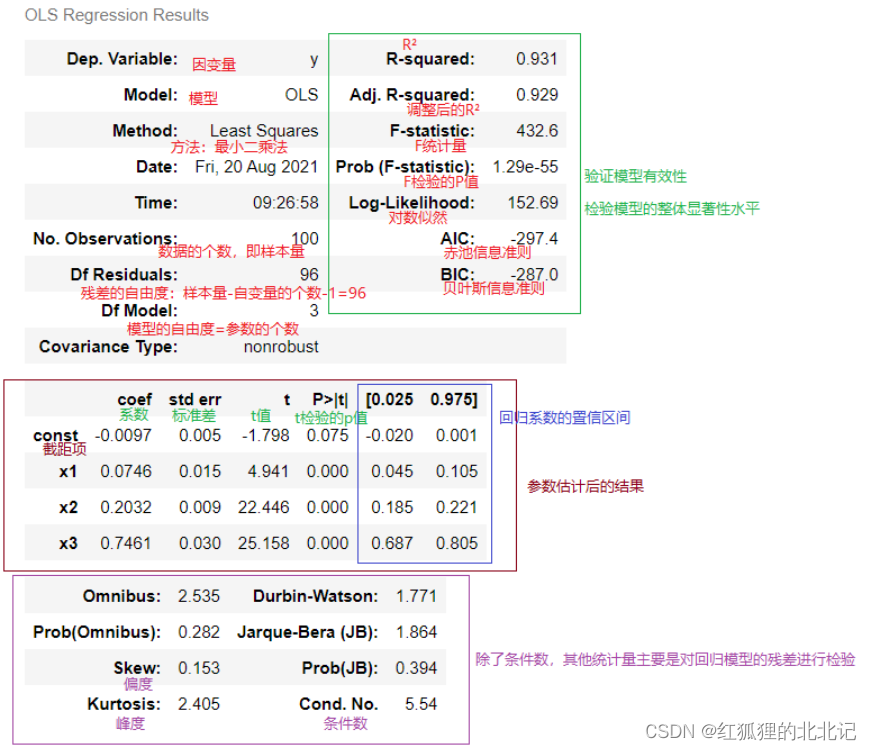
# 下面是进行参数估计，参数估计的主要目的是估计出回归系数，根据参数估计结果来计算统计量，
# 这些统计量主要的目的就是对我们模型的有效性或是显著性水平来进行验证。
results = model.fit()# fit拟合
results.summary()# summary方法主要是为了显示拟合的结果

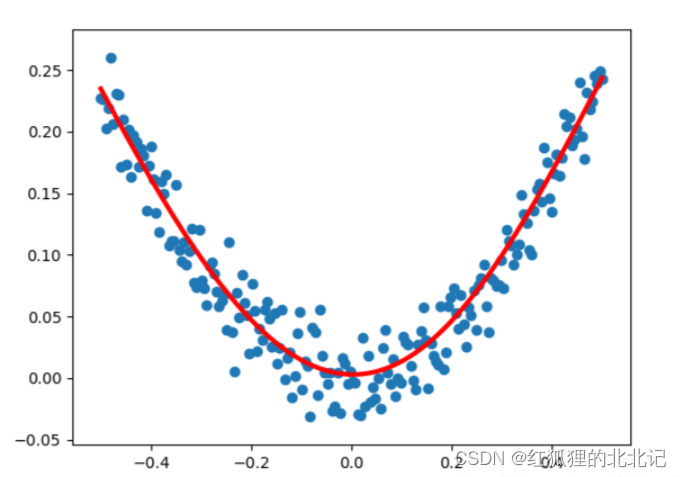
3.2非线性回归模型

非线性回归是线性回归的延伸，线性就是每个变量的指数都是 1，而非线性就是至少有一个变量的指数不是 1。生活中，很多现象之间的关系往往不是线性关系。选择合适的曲线类型不是一件轻而易举的工作，主要依靠专业知识和经验。

import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras

#建立随机数作为数据集
x_data = np.linspace(-0.5,0.5,200)  #从-0.5到0.5取均匀的200个数
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data)+noise

#使用keras的Sequential函数建立一个顺序模型
model = keras.Sequential()
#在模型中添加全连接层和激活函数
model.add(keras.layers.Dense(units=10,input_dim=1))
model.add(keras.layers.Activation('tanh'))
model.add(keras.layers.Dense(units=1))
model.add(keras.layers.Activation('tanh'))
 
#定义优化算法
sgd = keras.optimizers.SGD(learning_rate=0.3)
#优化方法：sgd（随机梯度下降算法）
#损失函数：mse（均方误差）
model.compile(optimizer=sgd,loss='mse')

for step in range(3001):
    #每次训练一个批次
    cost = model.train_on_batch(x_data,y_data)
    #每500个batch打印一次cost
    if step % 500 == 0:
        print('cost:',cost)

#x_data输入到网络中，得到预测值y_pred
y_pred = model.predict(x_data)
 
#显示随机点的结果
plt.scatter(x_data,y_data)
 
#显示预测点的结果
plt.plot(x_data,y_pred,'r-',lw=3)
plt.show()