©PaperWeekly 原创 · 作者 | 苏剑林
单位 | 追一科技
研究方向 | NLP、神经网络
在这篇文章中,我们将探讨一个被称为“梯度流(Gradient Flow)”的概念。简单来说,梯度流是将我们在用梯度下降法中寻找最小值的过程中的各个点连接起来,形成一条随(虚拟的)时间变化的轨迹,这条轨迹便被称作“梯度流”。在文章的后半部分,我们将重点讨论如何将梯度流的概念扩展到概率空间,从而形成“Wasserstein 梯度流”,为我们理解连续性方程、Fokker-Planck 方程等内容提供一个新的视角。

梯度下降
假设我们想搜索光滑函数 的最小值,常见的方案是梯度下降(Gradient Descent),即按照如下格式进行迭代:
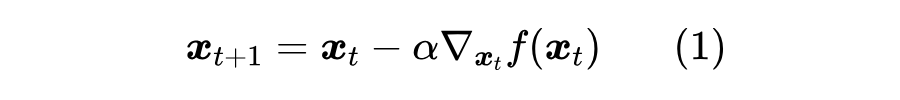
如果 关于 是凸的,那么梯度下降通常能够找到最小值点;相反,则通常只能收敛到一个“驻点”——即梯度为 0 的点,比较理想的情况下能收敛到一个极小值(局部最小值)点。这里没有对极小值和最小值做严格区分,因为在深度学习中,即便是收敛到一个极小值点也是很难得的了。
如果将 记为 ,将 记为,那么考虑 的极限,那么式(1)将变为一个 ODE:
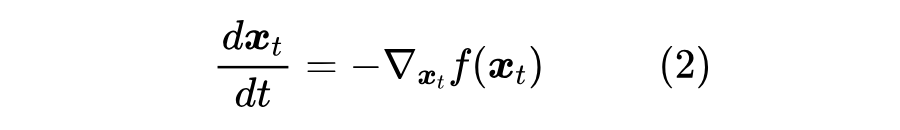
求解这个 ODE 所得到的轨迹 ,我们就称为“梯度流(Gradient Flow)”,也就是说,梯度流是梯度下降在寻找最小值过程中的轨迹。在式(2)成立前提下,我们还有:
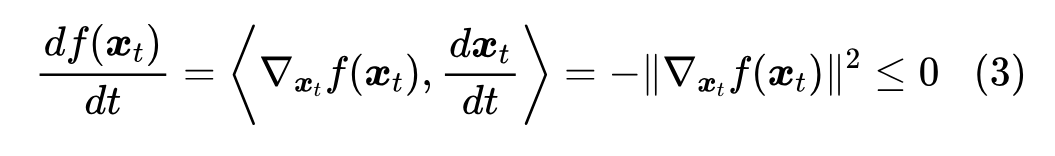
这就意味着,只要 ,那么当学习率足够小时,梯度下降总能往让 变小的方向前进。
更多相关讨论,可以参考之前的优化算法系列,如《从动力学角度看优化算法:从SGD到动量加速》、《从动力学角度看优化算法:一个更整体的视角》等。

最速方向
为什么要用梯度下降?一个主流的说法是“梯度的负方向是局部下降最快的方向”,直接搜这句话就可以搜到很多内容。这个说法不能说错,但有点不严谨,因为没说明前提条件——“最快”的“最”必然涉及到定量比较,只有先确定比较的指标,才能确定“最”的结果。
如果只关心下降最快的方向的话,梯度下降的目标应该是:
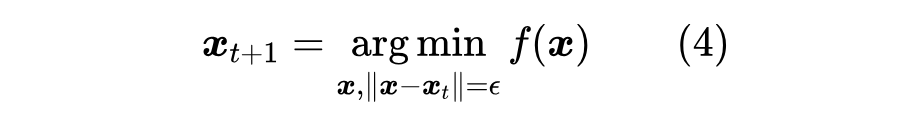
假设一阶近似够用,那么有
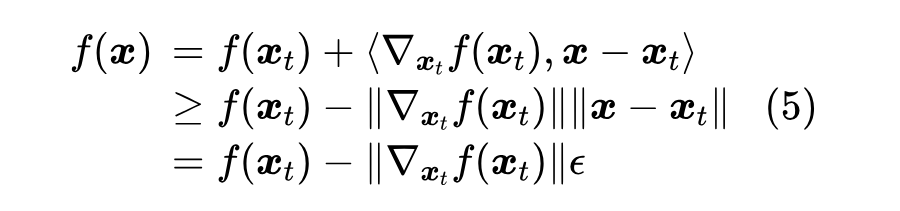
等号成立的条件是
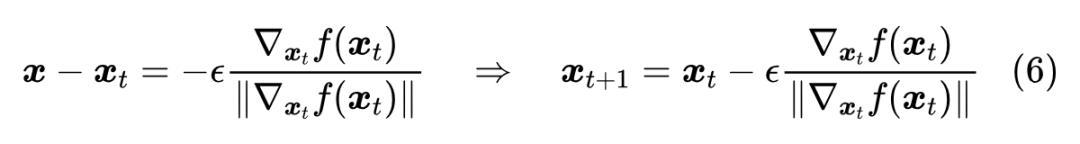
可以看到,更新方向正好是梯度的负方向,所以说它是局部下降最快的方向。然而,别忘了这是在约束条件 下得到的,其中 是欧氏空间的模长,如果换一个模长的定义,或者干脆换一个约束条件,那么结果就不一样了。所以,严谨来说应该是“在欧氏空间中,梯度的负方向是局部下降最快的方向”。

优化视角
式(4)是一个带约束优化,推广和求解起来都会比较麻烦。此外,式(4)的求解结果是式(6),也不是原始的梯度下降(1)。事实上,可以证明式(1)对应的优化目标是
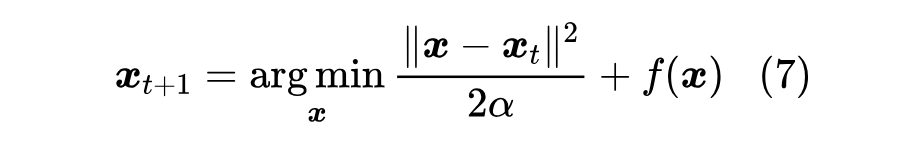
也就是说,将约束当成惩罚项加入到优化目标,这样就不用考虑求解约束,也容易推广。当 足够小时,第一项占主导,因此 需要足够小时第一项才会变得足够小,即最优点应该是很接近 的,于是我们可以在 处将 展开,得到
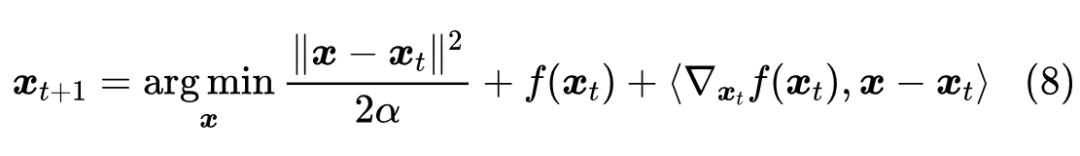
此时只是一个二次函数最小值问题,求解结果正是式(1)。
很明显,除了模长平方外,我们还可以考虑别的正则项,从而形成不同的梯度下降方案。比如,自然梯度下降(Natural Gradient Descent)使用的是 KL 散度作为正则项:
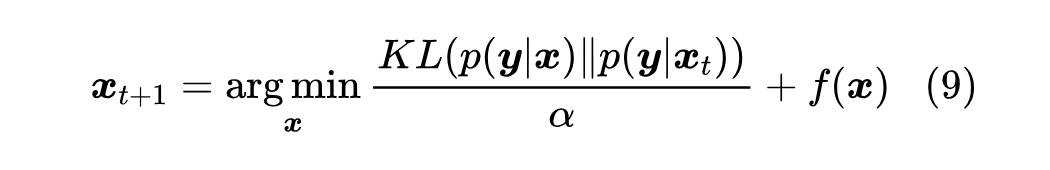
其中 是某个与 相关的概率分布。为了求解上式,同样在 处进行展开, 同样展开到一阶,但是 KL 散度比较特殊,它展开到一阶还是零(参考这里),所以至少要展开到二阶,总的结果是
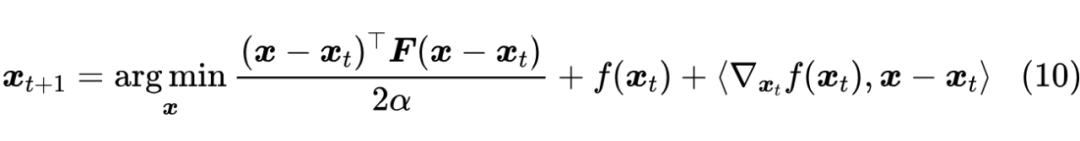
这里的 是 Fisher 信息矩阵 [1],计算细节就不展开了,过程也可以参考这里。现在上式本质上也是二次函数的最小值问题,结果为
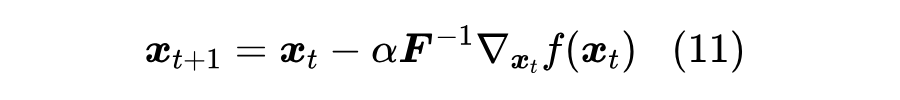
这就是所谓的“自然梯度下降”。

泛函入门
式(7)不仅可以将正则项一般化,还可以将求解目标一般化,比如推广到泛函。
“泛函”看起来让人“犯寒”,但事实上对于本站的老读者来说应该接触多次了。简单来说,普通多元函数就是输入一个向量,输出一个标量,泛函则是输入一个函数,输出一个标量,比如定积分运算:
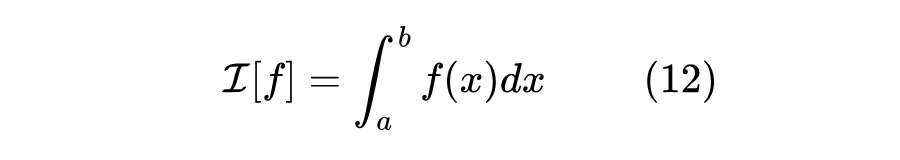
对于任意一个函数 , 的计算结果就是一个标量,所以 就是一个泛函。又比如前面提到的 KL 散度,它定义为
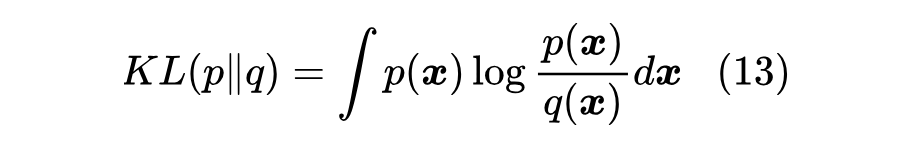
这里积分默认为全空间积分,如果固定 ,那么它就是关于 的泛函,因为 是一个函数,输入一个满足条件的函数, 将输出一个标量。更一般地,《f-GAN简介:GAN模型的生产车间》所介绍的 f 散度,也是泛函的一种,这些都是比较简单的泛函,更负责的泛函可能包含输入函数的导数,如理论物理的最小作用量 [2]。
下面我们主要关注的泛函的定义域为全体概率密度函数的集合,即研究输入一个概率密度、输出一个标量的泛函。

概率之流
假如我们有一个泛函 ,想要计算它的最小值,那么模仿梯度下降的思路,只要我们能求出它的某种梯度,那么就可以沿着它的负方向进行迭代。
为了确定迭代格式,我们沿着前面的思考,考虑推广式(7),其中 自然是替换为 ,那么第一项正则应该替换成什么呢?在式(7)中它是欧氏距离的平方,那么很自然想到这里也应该替换为某种距离的平方,对于概率分布来说,性态比较好的距离是 Wasserstein 距离(准确来说是“2-Wasserstein距离”):
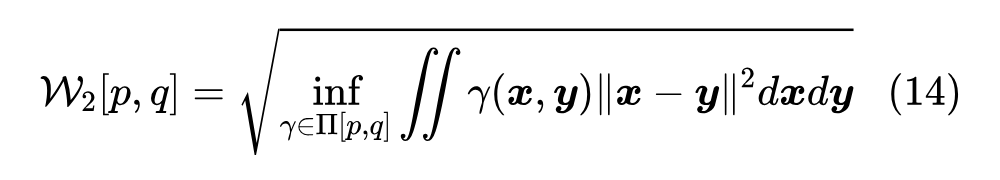
关于它的介绍,这里就不详细展开了,有兴趣的读者请参考《从Wasserstein距离、对偶理论到WGAN》。如果进一步将式(7)中的欧氏距离替换为 Wasserstein 距离,那么最终目标就是
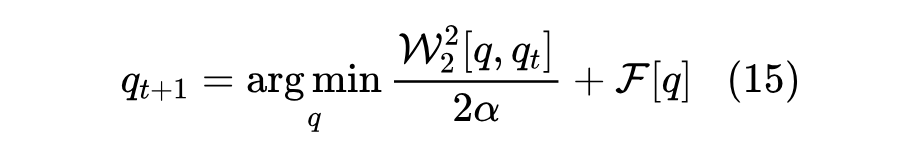
很抱歉,笔者没法简明给出上述目标的求解过程,甚至笔者自己也没完全理解它的求解过程,只能根据《Introduction to Gradient Flows in the 2-Wasserstein Space》[3]、《{Euclidean, Metric, and Wasserstein} Gradient Flows: an overview》[4] 等文献,直接给出它的求解结果为
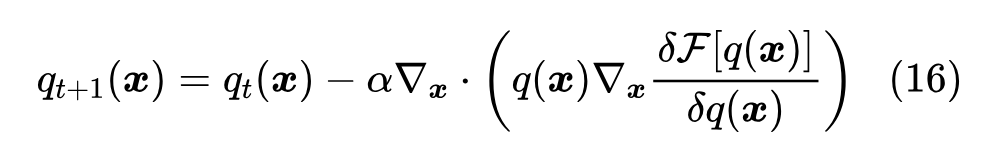
或者取极限后得到
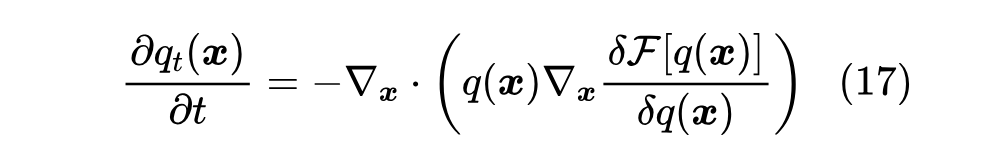
这就是 “Wasserstein 梯度流(Wasserstein Gradient Flow)”,其中 是 的变分导数,对于定积分泛函来说,变分导数就是被积函数的导数:
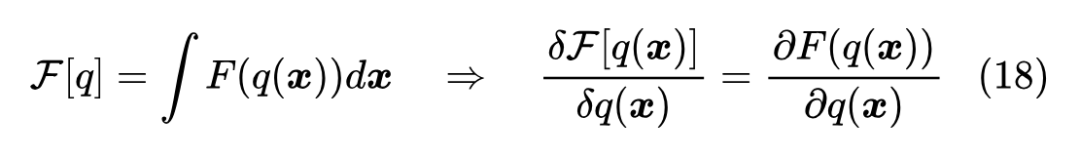

一些例子
根据《f-GAN简介:GAN模型的生产车间》, 散度的定义为
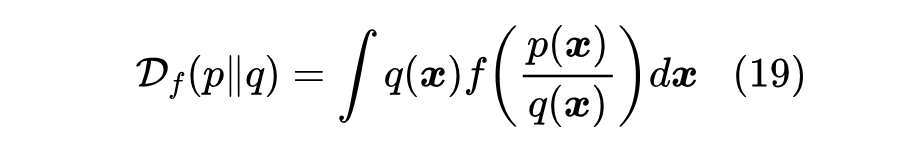
将 固定,设 ,那么得到
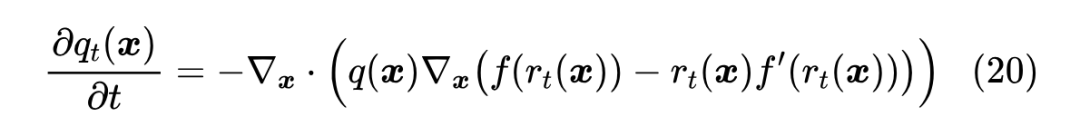
其中 。根据《测试函数法推导连续性方程和Fokker-Planck方程》[5] 的内容,上式具备连续性方程的形式,所以通过 ODE
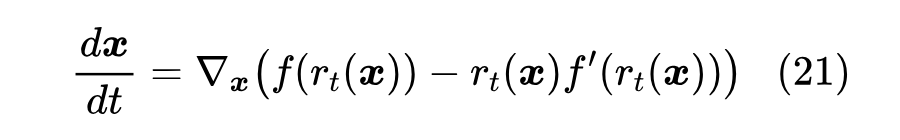
可以实现从分布 中采样,而根据前面的讨论,式(20)是最小化 的 散度的 Wasserstein 梯度流,当 时 散度为零,即 ,所以 时,上述 ODE 实现了从分布 采样。不过,这个结果目前来说只有形式上的意义,并没有实际作用,因为这意味着我们要知道分布 的表达式,还要从式(20)中解出 的表达式,然后才能算出 ODE 右端式子,从而完成采样,这个计算难度非常大,通常是没法完成的。
一个相对简单的例子是(逆)KL 散度,此时 ,代入式(20)得到
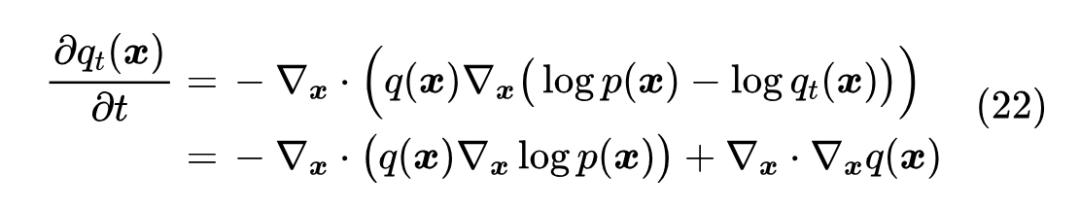
再次对比《测试函数法推导连续性方程和Fokker-Planck方程》[5] 的结果,这正好是个 Fokker-Planck 方程,对应于 SDE:
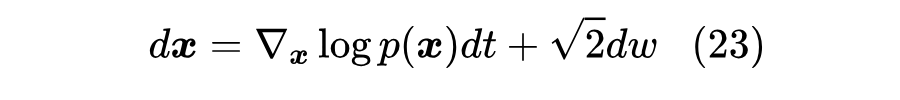
也就是说,如果我们知道 ,那么就可以实现用上式实现从 中采样,相比前面的 ODE,免除了求解 的过程,是一个相对可用的方案。

文章小结
本文介绍了梯度下降求最小值过程中的“梯度流”概念,其中包括向量空间的梯度流到概率空间的 Wasserstein 梯度流的拓展,以及它们与连续性方程、Fokker-Planck 方程和 ODE/SDE 采样之间的联系。

参考文献

[1] https://en.wikipedia.org/wiki/Fisher_information
[2] https://kexue.fm/archives/1304
[3] https://abdulfatir.com/blog/2020/Gradient-Flows/
[4] https://arxiv.org/abs/1609.03890
[5] https://kexue.fm/archives/9461
更多阅读




#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿

△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
·
·