⭐️ 环形链表 I 题目描述

给你一个链表的头节点 head ，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

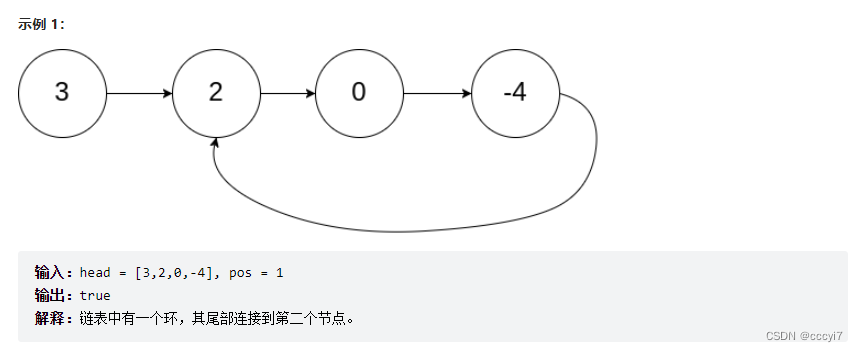
思路：快慢指针问题。我们可以声明一个 fast 指针（一次走两步），声明一个 slow 指针（一次走一步）。如果链表中存在环，那么 fast 指针和 slow 指针就会相遇，如果相遇则代表有环，否则 fast 指针会结束代表没环。

🌠 为什么快指针走两步，慢指针走一步可以相遇？

图：

假设 slow 进环后，fast 和 slow 距离是 $N$。这时候 fast 开始追击 slow ，fast 一次走两步，slow一次走一步，他们之间的距离每次缩小 $1$。N、N-1、N-2、...、2、1、0。最终他们相遇了，所以结论是肯定会相遇，因为他们的距离每次缩小$1$。

🌠 那快指针一次走三步，慢指针走一步可以相遇吗？

还是假设 slow 进环后，fast 和 slow 距离是 $N$。这时候 fast 一次走三步，slow 一次走一步，他们之间的距离每次缩小 $2$。

1. 当 $N$ 是偶数的情况：N、N-2、N-4、...、4、2、0 相遇追上了。
2. 当 $N$ 是奇数的情况：N、N-2、N-4、...、3、1、-1。这里 -1 意味着刚好错过了，但是此时 fast 是要超出 slow 一步，再假设环的大小是 $C$。那么现在 fast 和 slow 的距离刚好是 $C-1$步。又分为两种情况：
   • 如果 $C-1$ 是偶数的话，那么 fast 和 slow 就可以相遇。
   • 如果 $C-1$ 是奇数的话，那么 fast 就会重复上面是奇数的情况，永远不会相遇。

结论：当 fast 一次走三步，slow 一次走一步，不一定可以相遇。

---

leetcode链接：141.环形链表 I

⭕️ 代码：

bool hasCycle(struct ListNode *head) {
    struct ListNode * slow = head;
    struct ListNode * fast = head;
    
    // 考虑没有环的情况下，奇数和偶数个链表 fast 结束条件不同
    while (fast && fast->next) {
        fast = fast->next->next;
        slow = slow->next;

        if (fast == slow) {
            return true;
        }
    }

    return false;
}

⭐️ 环形链表 II 题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 NULL。不允许修改链表。
结论是当一个指针从 fast 和 slow 的相遇点 meet 开始走，一个指针从 head 位置开始走，最终 meet 和 head 会在入环点相遇。

🌠 为什么一个指针从相遇点走，一个指针从头走，他俩会在入环点相遇呢？

假设 head 到入环点的距离是 $L$ ，入环点到相遇点的距离是 $X$，而环的大小是 $C$。
首先 slow 进环之后，fast 在一圈之内，一定可以追上 slow！因为追击的过程他们距离每次缩小1，首先排除错过，而 slow 进环 fast 与其最大长度也只是 $C-1$，所以 slow 最多走不到半圈，fast 就会追上。
slow 走的路程：$L+X$
fast 走的路程：$L+N\ast C+X$   $(N>=1)$ 假设 slow 在进环前，fast 在环里转了 $N$ 圈。

所以 fast 走了 slow 2倍。

• $2\ast (L+X)=L+N\ast C+X$
• $L+X=N\ast C$
• $L=N\ast C-X$

所以 $L$ 的距离就是绕了 $N$ 圈之后到达 meet 的距离在减去 $X$ 的距离，就是入环点。
结论：一个指针从 meet 开始走，一个指针从 head 开始走，他们会在入环点相遇。

---

leetcode链接：142.环形链表 II

⭕️ 代码：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * slow = head;
    struct ListNode * fast = head;
    
    // 考虑没有环的情况下，奇数和偶数个链表 fast 结束条件不同
    while (fast && fast->next) {
        fast = fast->next->next;
        slow = slow->next;

        if (fast == slow) {
             struct ListNode * meet = fast;
             while (head != meet) {
                 head = head->next;
                 meet = meet->next;
             }

             return meet;
        }
    }

    return NULL;
}

---