在一个周日下午，夏天的雨稀里哗啦地下着
我躺在床上，捧着ipad看支持向量机
睡了好几个觉…支持向量机太好睡了
拉格朗日乘数法太好睡了
几何函数太好睡了
在我看来，支持向量机是目前学下来，最难以理解的内容
希望日后不要太难…脑子不支持的

1. 支持向量机的分类原理

支持向量积的原理，网上已经有很多人解释了。
支持向量机（SVM）——原理篇
机器学习笔记（五）：支持向量机（SVM）
支持向量机算法（SVM）详细讲解(含手推公式）
但即使看了原理篇，依然有绊倒自己的地方，或许是自己数学基础跟不上各大阿婆主，只好自己列出困惑的数学问题。

当数据集线性可分时，假设有一个线性函数能将数据集分类，这就是感知机模型该做的事：找到能让数据集线性划分的一个线性函数 $y=\sum w_i{x}_i+b$

但实际上，不一定只有一个线性函数，能线性划分数据集，那么哪个线性函数的划分效果更好呢？这就是支持向量机进一步要做的事。

支持向量机是以感知机为基础，进一步要求线性函数划分距离更宽：也就是线性函数两侧的数据集，距离最远，即求出线性函数对称两侧的最大宽度距离2d

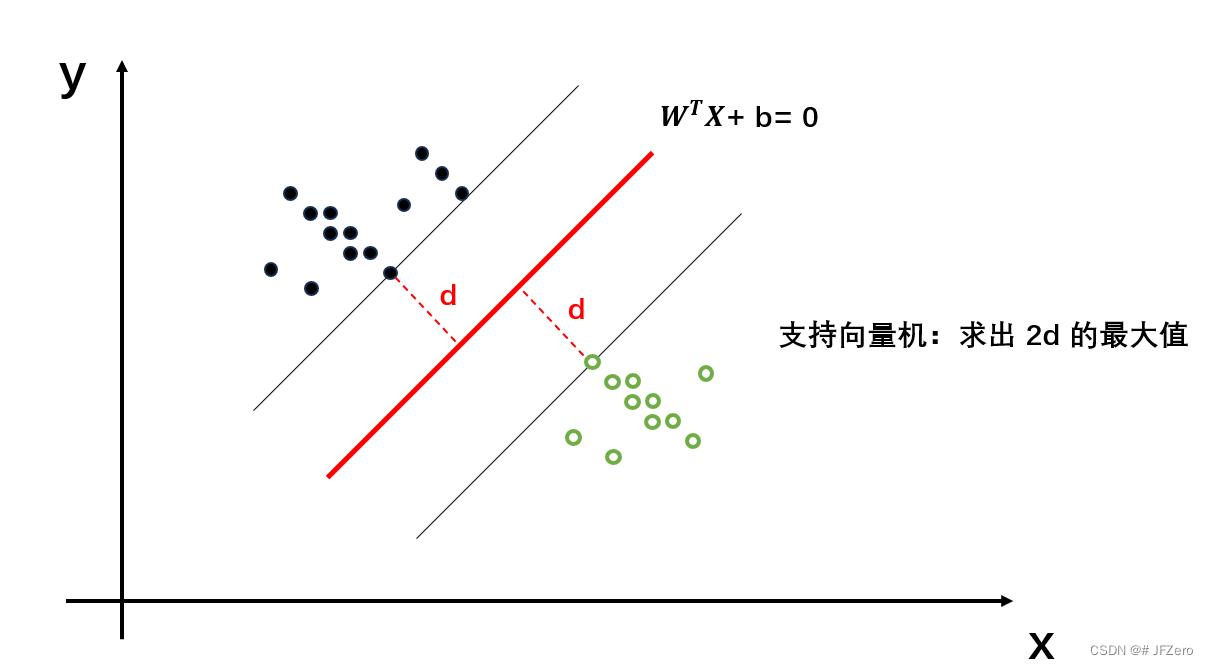
这挺好理解的，要想井水不犯河水，那就离得远远的。最好是一个天上，一个地下，互不打扰
比如深海里的鲨鱼，和高空上的雄鹰，这俩就不是一类…因为离得太远…好吧，这个比喻纯粹扯淡了
从逻辑上来说，空间距离越大，差异越大，这是公认事实。

但要怎么求出2d的最大值呢？

这就要涉及到我困惑很久的第一个问题：点到线（点到面或超平面）的距离计算公式

1.2 第一个数学困惑：点到线（面）的距离公式

$d=\frac{|W^{T}X+b|}{||W|{|}_2}$

为什么是这个公式？？这让我困惑很久…数学没学好

我试着从几何的角度，从一元线性函数、二元线性函数图像上去推导，但仅仅能推导到二元，一旦涉及到三元【三维空间】，我脑子就废了

后来，无意间看到一个博主的解释

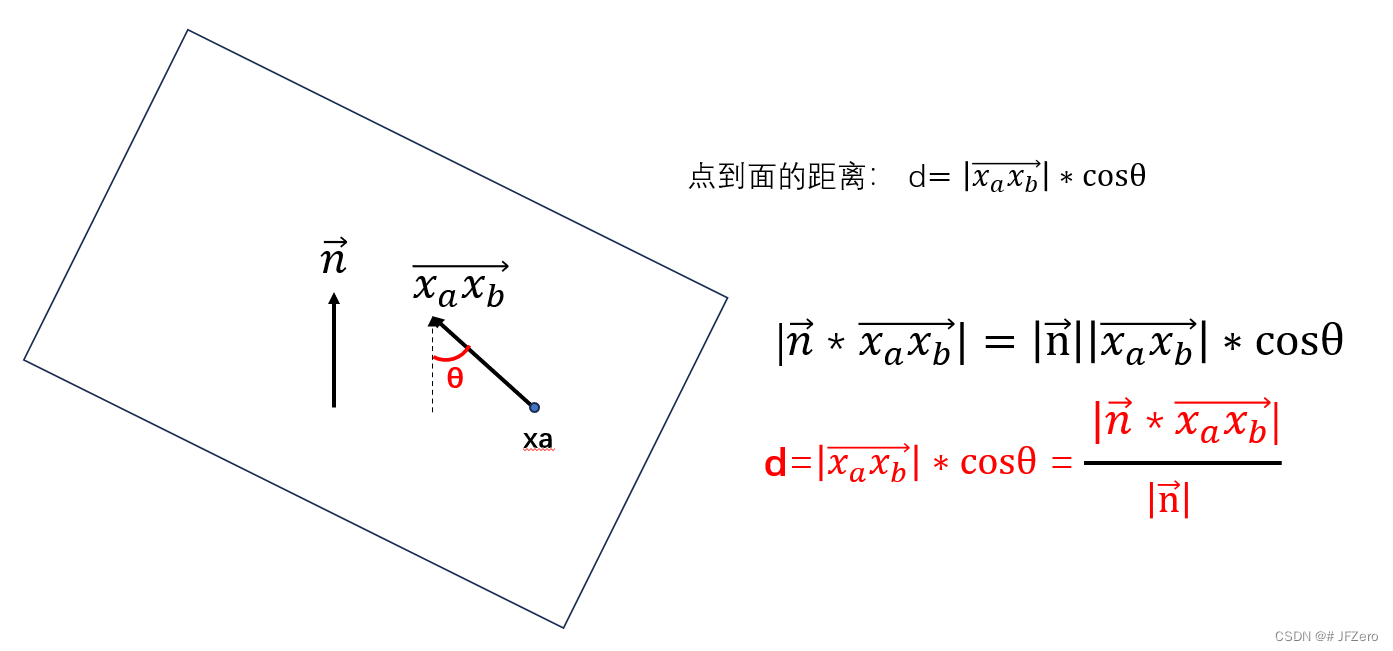
恍然大悟，哦~~~~
但哦什么呢。。。。这个法向量n是怎么算的

如果超平面的函数为 $A{x}_1+B{x}_2+C{x}_3+D=0$
求点$x_b$到超平面 $A{x}_1+B{x}_2+C{x}_3+D=0$的距离，（设点$x_a$位于平面上）

那个博主说法向量设为 $n^{\to }=(A,B,C)$

则向量 ${x_a{x}_b}^{\to }=(x_{a1}-x_{b1},x_{a2}-x_{b2},x_{a3}-x_{b3})$

$d=\frac{{x_a{x}_b}^{\to }\ast n^{\to }}{|n^{\to }|}=\frac{A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})}{\sqrt{A^2+B^2+C^2}}$

由于点$x_a$位于平面上，因此$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}+D=0$
则$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}=-D$

则分子部分：$A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})$
$=-(A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D)$

整合起来的$d=\frac{|{x_a{x}_b}^{\to }\ast n^{\to }|}{|n^{\to }|}=\frac{|A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})|}{\sqrt{A^2+B^2+C^2}}=\frac{|-(A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D)|}{\sqrt{A^2+B^2+C^2}}$

这不就是 $d=\frac{|W^{T}X+b|}{||W|{|}_2}$ 的公式了嘛！！！

但要注意：$d=\frac{|W^{T}X+b|}{||W|{|}_2}$公式，表示的是点到中间分类函数线的距离

不同的点，计算出的d值是不同的。

顿悟!!
但问题又来了

凭什么法向量可以设为 $n^{\to }=(A,B,C)$

这也是困惑很久的小问题，但也可以证明：首先知道法向量是垂直于平面的

求法向量$n^{\to }=(x_{n1},x_{n2},x_{n3})$

那么当平面上有两个不共线的向量 $Q^{\to }=(x_{q1},x_{q2},x_{q3})$, $F^{\to }=(x_{f1},x_{f2},x_{f3})$

法向量与这两个向量的乘积均为0
$n^{\to }\ast Q^{=}{x}_{n1}{x}_{q1}+x_{n2}{x}_{q2}+x_{n3}{x}_{q3}=0$
$n^{\to }\ast F^{=}{x}_{n1}{x}_{f1}+x_{n2}{x}_{f2}+x_{n3}{x}_{f3}=0$
上述两个式子相减得到$x_{n1}(x_{f1}-x_{q1})+x_{n2}(x_{f1}-x_{q2})+x_{n3}(x_{f1}-x_{q3})=0$

并且由于向量$Q^{\to }和F^{\to }$都在平面上，因此:
$A{x}_{q1}+B{x}_{q2}+C{x}_{q3}+D=0$
$A{x}_{f1}+B{x}_{f2}+C{x}_{f3}+D=0$
上述两个式子相减$A(x_{f1}-x_{q1})+B(x_{f1}-x_{q2})+C(x_{f1}-x_{q3})=0$

综合可得：
$x_{n1}(x_{f1}-x_{q1})+x_{n2}(x_{f1}-x_{q2})+x_{n3}(x_{f1}-x_{q3})=0$
$A(x_{f1}-x_{q1})+B(x_{f1}-x_{q2})+C(x_{f1}-x_{q3})=0$

因此，可以设$x_{n1}=A$,$x_{n2}=B$,$x_{n3}=C$
因此法向量可以设为函数的系数！！！！

又悟了！！！数学渣渣的困惑。。。终于悟了

1.3 第二个数学困惑：距离公式的分子用1来计算

教科书，包括很多up主，在求解最大宽度距离$2d=\frac{2|W^{T}X+b|}{||W|{|}_2}$时，又转化为 求$\frac{2}{||W|{|}_2}$的最大值

why??

其实我也悟了。。。但太困了。。。明天再搞吧

公式推导一下：

将划分数据集的分类函数为$A{x}_1+B{x}_2+C{x}_3+D=0$

而两侧对称的边界函数分为设为：

• $A{x}_1+B{x}_2+C{x}_3+D=Q$，移项得$A{x}_1+B{x}_2+C{x}_3+D-Q=0$
• $A{x}_1+B{x}_2+C{x}_3+D=-Q$，移项得$A{x}_1+B{x}_2+C{x}_3+D+Q=0$

这两个函数之间的距离，并不是2Q，而是 $\frac{2Q}{||W|{|}_2}$

为什么是这样呢？

假设
点$x_a$位于$A{x}_1+B{x}_2+C{x}_3+D-Q=0$边界函数上
点$x_b$位于$A{x}_1+B{x}_2+C{x}_3+D+Q=0$边界函数上
$A{x}_1+B{x}_2+C{x}_3+D-Q=0$和$A{x}_1+B{x}_2+C{x}_3+D+Q=0$是平行的边界函数
设点$x_a$和点$x_b$的连线，垂直于这两条边界函数，则向量$x_a{x}_b^{\to }$则相当于这两个边界函数的法向量，同时模|$x_a{x}_b^{\to }$|表示两个边界函数的距离。

现在要求的就是模|$x_a{x}_b^{\to }$|，即两个边界函数的距离。

法向量设为 $n^{\to }=(A,B,C)$

则向量 ${x_a{x}_b}^{\to }=(x_{a1}-x_{b1},x_{a2}-x_{b2},x_{a3}-x_{b3})$

$d_{边界}=\frac{{x_a{x}_b}^{\to }\ast n^{\to }}{|n^{\to }|}=\frac{A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})}{\sqrt{A^2+B^2+C^2}}$

由于点$x_a$有$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}+D-Q=0$
点$x_b$有$A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D+Q=0$
则上述两式相减可得：$A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})-2Q=0$

则$d_{边界}=\frac{|{x_a{x}_b}^{\to }\ast n^{\to }|}{|n^{\to }|}=\frac{|A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})|}{\sqrt{A^2+B^2+C^2}}=\frac{2Q}{\sqrt{A^2+B^2+C^2}}$

因此，两个边界函数的公式可对应为

• $W^{T}X+b=Q$
• $W^{T}X+b=-Q$
  且两个边界函数的距离为$\frac{2Q}{||W|{|}_2}$

而实际边界函数的W、b系数同比例增大或减小，对函数是毫无影响的

就比如2x + 4 = 0 与 x+2 = 0 本质都是相同的函数。

因此可对两个边界函数的W和b参数进行同比例的缩放

• $W^{T}X+b=Q$，变为${\frac{W}{Q}}^{T}X+\frac{b}{Q}=1$
• $W^{T}X+b=-Q$，变为${\frac{W}{Q}}^{T}X+\frac{b}{Q}=-1$

此时，系数更新为$W=\frac{W}{Q}$，$b=\frac{b}{Q}$
因此两个边界函数最终变为了

• $W^{T}X+b=1$
• $W^{T}X+b=-1$

并且两个边界函数的距离为 $d_{边界}=\frac{2}{||W|{|}_2}$

至此，证成！！！
妈呀…应该是对的吧！！！

但其实我有个困惑，最初证明的点到线（面）的距离公式，以及两个边界函数的距离公式，分别有什么意义呢？

支持向量机，到底是要求距离中间分类线最近的点到线（面）的距离最大，还是要求两个边界函数的距离最大呢？

本质上看，这两个要求其实都是同一个要求，但实际上这两个要求所进行的计算方式是不同的。

如果是要求距离中间分类线最近的点，到中间分类函数的距离最大，那就必须先能求出中间分类函数——但实际我们没有边界函数，是没办法求出中间分类函数的。

- 因此，应该是要求两个边界函数的距离最大，因为两个边界函数的距离，实际是可以根据某个分类函数来求的。

听起来很绕口，但实际就是我们可以根据感知机模型，求出一个分类函数，但这个分类函数并不一定是能将数据集平均分的函数

但这个不怎么完美的函数，却是一个有着明确参数W的函数，那么假设两个边界函数分别在这个分类函数的两侧【注：两个边界函数未必对称分布在分类函数的两边】

我们无需计算出具体的参数b，只要根据参数W，就可以求出两个边界函数的距离

• $d_{边界}=\frac{2}{||W|{|}_2}$
  但要注意，边界函数是要能够将数据集分类的，因此边界函数的还要满足以下两个条件
• $W^{T}X+b\ge 1$时，$y=1$，要求分类正确，即$y\ast (W^{T}X+b)\ge 1$
• $W^{T}X+b\le -1$时，$y=-1$，要求分类正确，即$y\ast (W^{T}X+b)\ge 1$
• 整合起来就是两条边界函数均满足：$y\ast (W^{T}X+b)\ge 1$

因此，我们只需求出$d_{边界}$的最大值，并且满足条件$y\ast (W^{T}X+b)\ge 1$，即可得到模型的最优解。

那么究竟要怎么在有条件限制的情况下，求出极值呢？
这就涉及到拉格朗日乘数法了
这痛苦的让人哭泣的拉格朗日
明天继续吧！！

• 求$d_{边界max}=\frac{2}{||W|{|}_2}$，实际相当于求 $\frac{W^2}{2}$的最小值

要是换以前，求最小值，要么用求导法或是用梯度下降法，就可以实现。
但现在不行了，因为求最小值时，是有条件约束的。

如何求条件约束下的极小值呢？

1.4 第三个数学困惑：拉格朗日乘数法的数理推导

这就要用到号称“条件极值杀手”的【拉格朗日乘数法】了。

死脑筋用拉格朗日乘数法，其实会比较简单，
但真的要理解拉格朗日乘数法，真的是头疼

首先，当要求的原函数为f(x,y)，条件约束为等式约束g(x,y)=0时，求条件约束下的原函数极小值。

• 原函数：$f(x,y)$
• 等式约束条件：$g(x,y)=0$
• 求 $min(f(x,y))$

拉格朗日乘数法的计算过程为求$L(x,y)=f(x,y)+\lambda g(x,y)$的极值

• $L_x^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }$
• $L_y^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }$
• $L_{\lambda }^{\prime }=g(x,y)$
• 并解出x,y,λ的值，其中 x,y就是可能的符合约束条件下的极小值

看到这的时候，我直觉是合理的，但不知道是如何得出这样的计算过程，并产生了几个问题：

• 为什么有λ？
• 为什么可以构成拉格朗日函数？
• 为什么求出拉格朗日函数极值，就可以求出符合约束条件的极小值？？？

所以自己又翻阅了很多知乎阿婆主的各种解释
终于功夫不负爱搜索的人

很多人的解释是：用等高线来绘制原函数f(x,y)时，会呈现层层嵌套的圈圈，然后绘制g(x,y)时，很多人却又不是用等高线来绘制g(x,y)，然后很多人的解析就直接说g(x,y)取到极值的时候（与f(x,y)相切），就取到了符合约束条件的最小值。

说实话，几何法我还是不太理解

找到有个up主的数理推导：
通过g(x,y)=0，说明这个g(x,y)是隐函数，然后我们可设为显函数y = φ(x)

然后代入f原函数：$z=f(x,\phi (x))$，用z表示代入后的函数表达，使得z与原函数f区分开

$z_x^{\prime }=\frac{əf}{əx}+\frac{əf}{əy}\frac{d\phi (x)}{dx}=f_x^{\prime }+f_y^{\prime }\ast {\phi }_x^{\prime }$

根据隐函数求导法则：$\frac{dy}{dx}=-\frac{F_x^{\prime }}{F_y^{\prime }}$为什么隐函数求导法则是这样的，后续再证明
则知道$\frac{dy}{dx}={\phi }_x^{\prime }=-\frac{g_x^{\prime }}{g_y^{\prime }}$

因此$z_x^{\prime }=f_x^{\prime }+f_y^{\prime }\ast {\phi }_x^{\prime }=f_x^{\prime }-f_y^{\prime }\ast \frac{g_x^{\prime }}{g_y^{\prime }}=f_x^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_x^{\prime }$

设$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}，则有f_x^{\prime }(x,y)=f_x^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }$

而此时，y的偏导数为$z_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=f_y^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_y^{\prime }=0$

融入了约束条件的函数f求得极值点，需要令x,y的偏导数均为0

• $要使z_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }=0，则要求\lambda =-\frac{f_x^{\prime }}{g_x^{\prime }}$

此时，要求的λ既要等于$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}$，又要求$\lambda =-\frac{f_x^{\prime }}{g_x^{\prime }}$

那么就需要$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$因此可推出：$\frac{f_x^{\prime }}{f_y^{\prime }}=\frac{g_x^{\prime }}{g_y^{\prime }}$
em。。。这式子很整齐，但这是个什么式子呢？？？？
根据隐函数的求导法则可知$\frac{f_y^{\prime }}{f_x^{\prime }}=-\frac{dy}{dx}$, $\frac{g_y^{\prime }}{g_x^{\prime }}=-\frac{dy}{dx}$
所以，$\frac{f_x^{\prime }}{f_y^{\prime }}=\frac{g_x^{\prime }}{g_y^{\prime }}$可以表示f(x,y)和g(x,y)的切线斜率相等
哇！！！这不就出来了吗！！！这不就是很多人用几何作图来表示的，为什么f(x,y)和g(x,y)在两函数的切线处取到极值吗!!!!用数学推导应该是这样证明的吧！！！！

总之，当$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$，且$\frac{f_y^{\prime }}{f_x^{\prime }}=\frac{g_y^{\prime }}{g_x^{\prime }}$时，得到两个方程：

• $z_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }=0$
• $z_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=0$
  对这两个式子左右两边分别乘以dx和dy，得到：
• $z_x^{\prime }dx=f_x^{\prime }dx+\lambda \ast g_x^{\prime }dx=\frac{əf}{əx}dx+\lambda \ast \frac{əg}{əx}dx=0$
• $z_y^{\prime }dy=f_y^{\prime }dy+\lambda \ast g_y^{\prime }dy=\frac{əf}{əy}dy+\lambda \ast \frac{əg}{əy}dy=0$
  对上述两个式子左右两边相加，得到：
• $z_x^{\prime }dx+z_y^{\prime }dy=\frac{əf}{əx}dx+\frac{əf}{əy}dy+\lambda \ast \frac{əg}{əx}dx+\lambda \ast \frac{əg}{əy}dy=0$
  对上述式子左右两边进行积分
• $z(x,y)=f(x,y)+\lambda g(x,y)$

而这个z函数，正是我们最后的拉格朗日函数$L(x,y)=f(x,y)+\lambda g(x,y)$

将g(x,y)=0约束条件转变为显示函数y = φ(x)，并融入原函数f(x,y)后，原函数f(x,y)不再是那个自由自在的纯粹的原函数了，它有了条件约束就称为拉格朗日函数$L(x,y)=f(x,\phi (x))$

并且当$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$时，且$\frac{f_y^{\prime }}{f_x^{\prime }}=\frac{g_y^{\prime }}{g_x^{\prime }}$，即原函数f(x,y)与约束条件g(x,y)函数相切时，下列式子成立，即可根据下列式子，求出x,y,λ后，求出拉格朗日函数的极值

• $L_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }=0$
• $L_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=0$
• $L_{\lambda }^{\prime }=g(x,y)=0$

我天呐！！！！我感觉完成了一大壮举！！！虽然我觉得偏导数、导数符号可能稍微有点儿问题
但没关系啊。。。至少，在我目前的认知层面来说。。。能圆过去

主要参照了两篇文章，并结合理解（其实这两篇文章中间都有我不理解的地方，但这么一相互融合理解，忽然就懂了呀！）
拉格朗日乘数法推导
拉格朗日乘数法理解

但问题尚未结束，因为之前引用了隐函数求导法则，但还不知道隐函数求导法则究竟是怎么推导出来的

1.4 第四个数学困惑：隐函数求导法则的公式推导

拉格朗日乘数法

2.支持向量机的数学推导