子数组的最小值之和
- leetcode907. 子数组的最小值之和
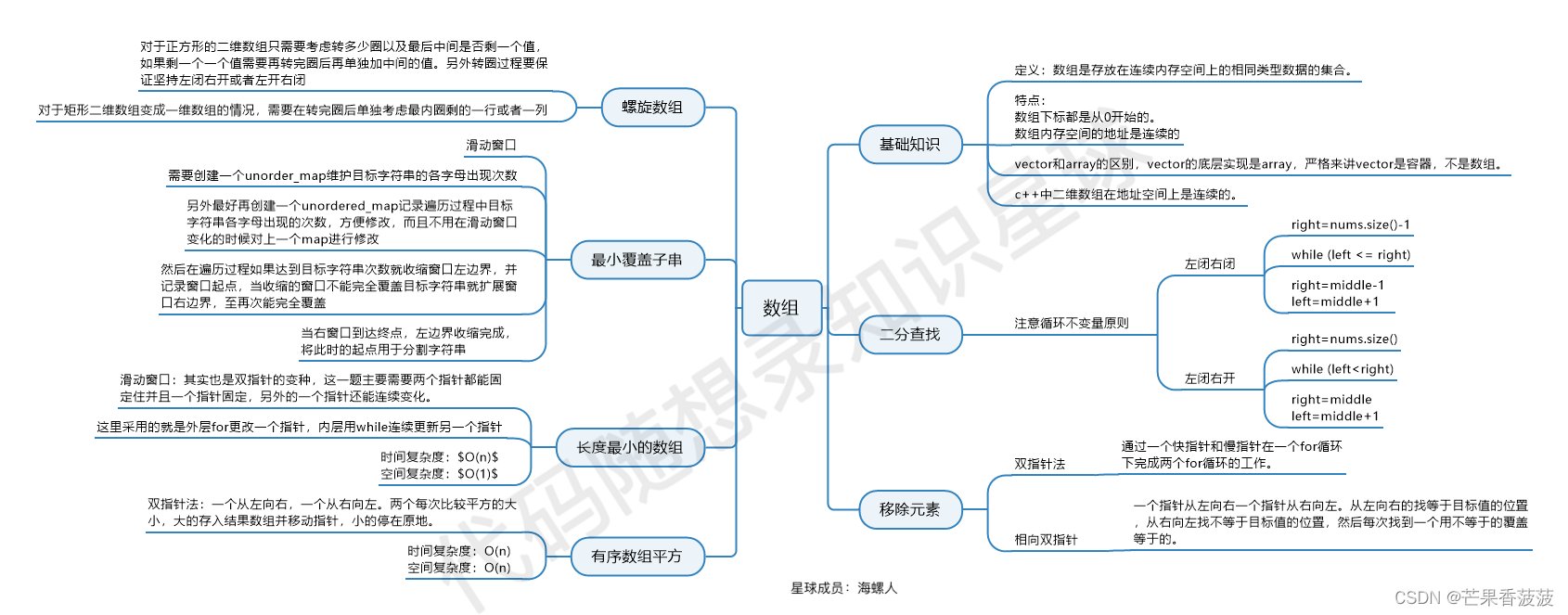
- 题目描述
- 单调栈解法一
- 代码演示
- 单调栈解法二
- 单调栈专题
leetcode907. 子数组的最小值之和
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/sum-of-subarray-minimums
题目描述
给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。
由于答案可能很大,因此 返回答案模 10^9 + 7 。
示例 1:
输入:arr = [3,1,2,4]
输出:17
解释:
子数组为 [3],[1],[2],[4],[3,1],[1,2],[2,4],[3,1,2],[1,2,4],[3,1,2,4]。
最小值为 3,1,2,4,1,1,2,1,1,1,和为 17。
示例 2:
输入:arr = [11,81,94,43,3]
输出:444
提示:
1 <= arr.length <= 3 * 104
1 <= arr[i] <= 3 * 104
单调栈解法一
由于我们是从子数组中取最小值来进行累加,即参与答案构成的每个数必然某个具体的。
因此我们可以将原问题转化为「考虑统计每个对答案的贡献」。
对于某一个
而言,我们考虑其能够作为哪些子数组的最小值。
我们可以想象以
为中心,分别往两端进行拓展,只要新拓展的边界不会改变「
为当前子数组的最小值」的性质即可。
换句话说,我们需要找到
作为最小值的最远左右边界,即找到
左右最近一个比其小的位置 l 和 r。
在给定序列中,找到任意
近一个比其大/小的位置,可使用「单调栈」进行求解。
到这里,我们会自然想到,通过单调栈的方式,分别预处理除 l 和 r 数组:
l[i] = loc 含义为下标 i 左边最近一个比 arr[i] 小的位置是 loc(若在
左侧不存在比其小的数,则 loc = -1)
r[i] = loc 含义为下标 i 右边最近一个比 arr[i] 小的位置是 loc(若在
左侧不存在比其小的数,则 loc = n)
当我们预处理两数组后,通过简单「乘法原理」即可统计以
为最小值时,子数组的个数:
包含 的子数组左端点个数为个包含的子数组右端点个数为个子数组的个数子数组最小值 ,即是当前 对答案的贡献:
统计所有
对答案的贡献即是最终答案,但我们忽略了「当 arr 存在重复元素,且该元素作为子数组最小值时,最远左右端点的边界越过重复元素时,导致重复统计子数组」的问题。
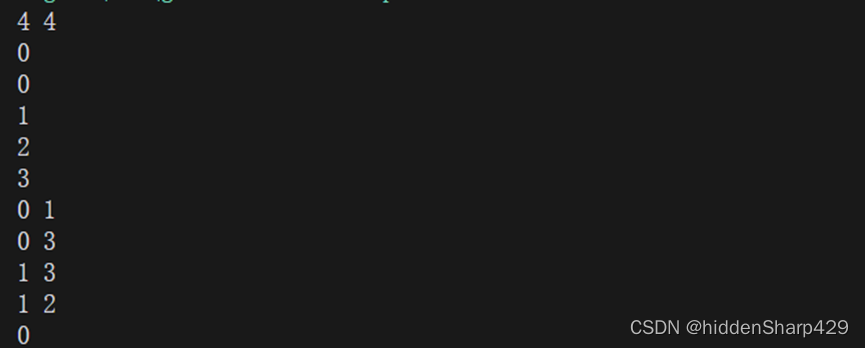
看图理解:
为了消除这种重复统计,我们可以将「最远左右边界」的一端,从「严格小于」调整为「小于等于」,从而实现半开半闭的效果。
代码演示
/**
* 子数组最小值之和
* @param arr
* @return
*/
public static int sumSubarrayMins(int[] arr) {
int[] stack = new int[arr.length];
int[] left = nearLessEqualLeft(arr, stack);
int[] right = nearLessEqualRight(arr, stack);
long ans = 0;
for (int i = 0; i < arr.length;i++){
long start = i - left[i];
long end = right[i] - i;
ans += start * end * (long)arr[i];
ans %= 1000000007;
}
return (int)ans;
}
/**
* 记录比当前数字小的左边界
* @param arr
* @param stack
* @return
*/
public static int[] nearLessEqualLeft(int[] arr, int[] stack) {
int N = arr.length;
int[] left = new int[N];
int size = 0;
for (int i = N - 1; i >= 0;i--){
while (size != 0 && arr[stack[size - 1]] >= arr[i]){
left[stack[--size]] = i;
}
stack[size++] = i;
}
while (size != 0){
left[stack[--size]] = -1;
}
return left;
}
/**
* 记录比当前数字小的右边界
* @param arr
* @param stack
* @return
*/
public static int[] nearLessEqualRight(int[]arr,int[]stack){
int N = arr.length;
int[] right = new int[N];
int size = 0;
for (int i = 0; i < N;i++){
while (size != 0 && arr[stack[size - 1]] > arr[i]){
right[stack[--size]] = i;
}
stack[size++] = i;
}
while (size != 0){
right[stack[--size]] = N;
}
return right;
}
单调栈解法二
可以对获取左右边界位置的方法,放在一起,进行优化下.
class Solution {
int MOD = (int)1e9+7;
public int sumSubarrayMins1(int[] arr) {
int n = arr.length, ans = 0;
int[]d = new int[arr.length];
int size = -1;
for (int r = 0; r <= n; r++) {
int t = r < n ? arr[r] : 0;
while (size != -1 && arr[d[size]] >= t) {
int cur = d[size--];
int l = size == -1 ? -1 : d[size];
int a = cur - l, b = r - cur;
ans += a * 1L * b % MOD * arr[cur] % MOD;
ans %= MOD;
}
d[++size] = r;
}
return ans;
}
}
单调栈专题
单调栈的实现-单调递减栈和单调递增栈
leetcode1856. 子数组最小乘积的最大值
leetcode84. 柱状图中最大的矩形
leetcode.85. 最大矩形
leetcode42. 接雨水
leetcode739. 每日温度
leetcode.1504. 统计全 1 子矩形