【数据结构与算法】查找课后习题

news2024/9/19 11:02:56

题目

下面一共有4道有关查找的课后习题，全部都是思路题、画图题并不是完整的算法设计题故在此就一起列举出来了~

1. 已知一个有序表的表长为8N，并且表中没有关键字相同的记录

假设按如下所述方法查找一个关键字等于给定值K的记录：先在第8,16,24,…,8K,…,8N个记录中进行顺序查找，或者查找成功，或者由此确定出一个继续进行折半查找的范围。画出描述上述查找过程的判定树，并求等概率查找时查找成功的平均查找长度。

解答

该查找过程的判定树如下
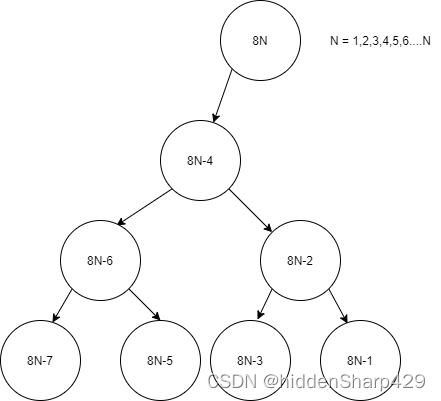
在这里插入图片描述
等概率查找时查找成功的平均查找长度为 $\frac{N+1)}{2}+ \frac{1+2*2+3*4}{8}$

2. 请对长度为10 的表: (22,45,56,12,33,57,88,94,44,11)画出构造平衡二叉树的过程

解答

第一步：插入22

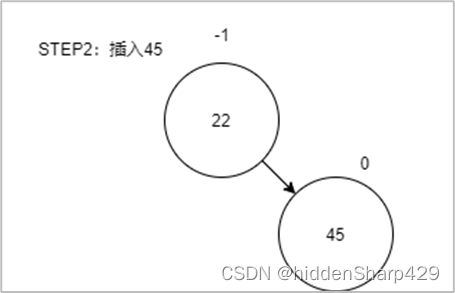
在这里插入图片描述

第二步：插入45

在这里插入图片描述

第三步：插入56（此时出现了不平衡）

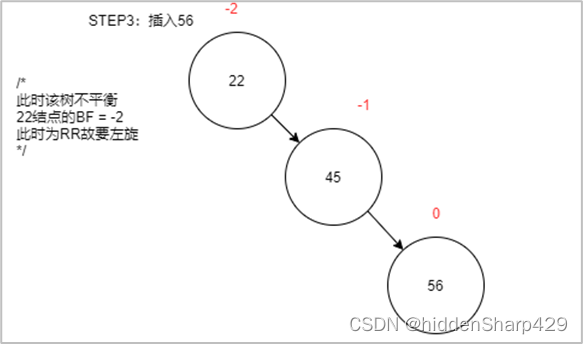
在这里插入图片描述

第四步：左旋22

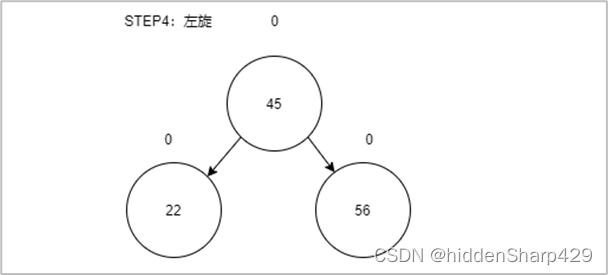
在这里插入图片描述

第五步：插入12

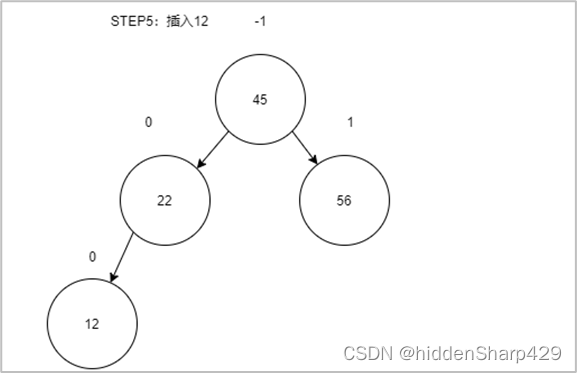
在这里插入图片描述

第六步：插入33

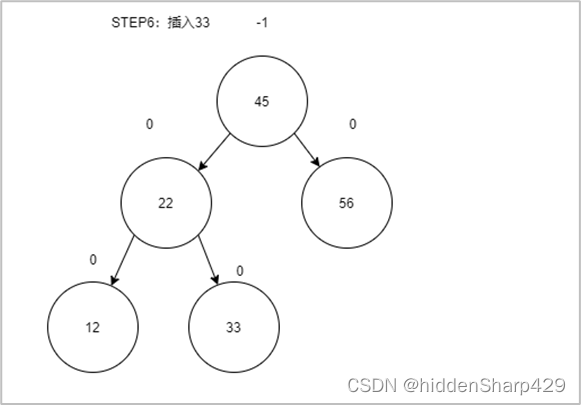
在这里插入图片描述

第七步：插入57

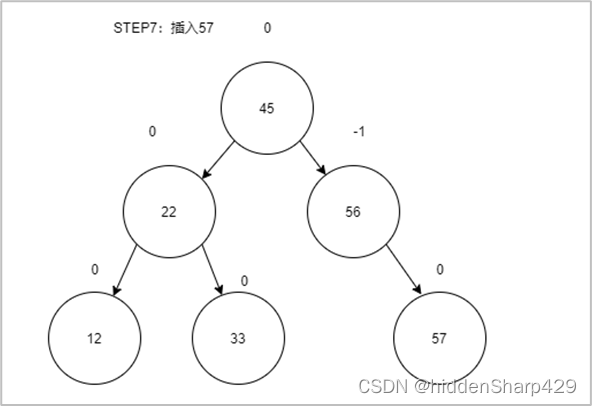
在这里插入图片描述

第八步：插入88（此时出现了不平衡）

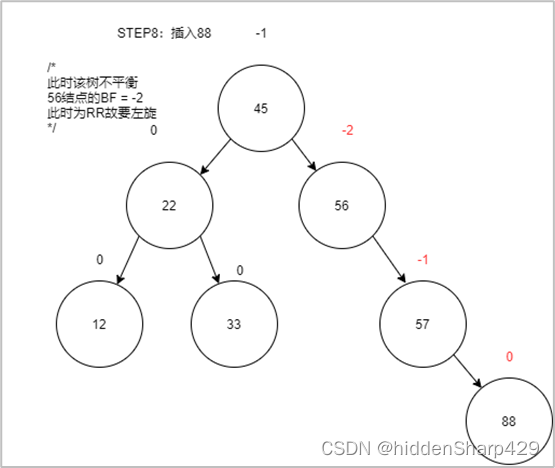
在这里插入图片描述

第九步：左旋

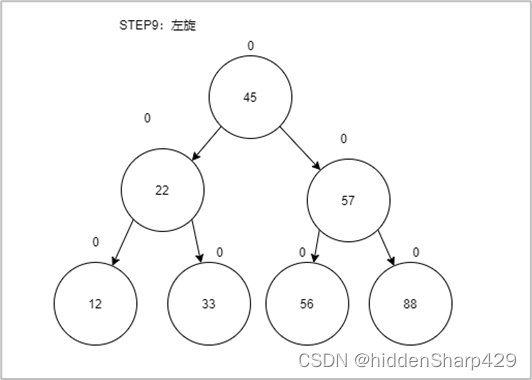
在这里插入图片描述

第十步：插入94

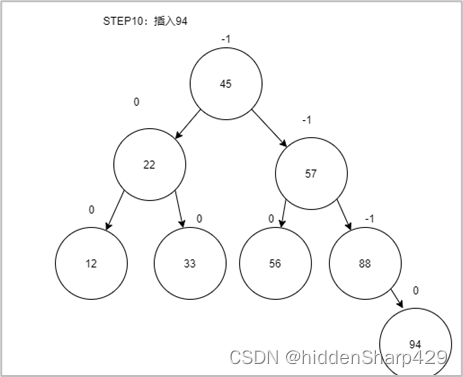
在这里插入图片描述

第十一步：插入44

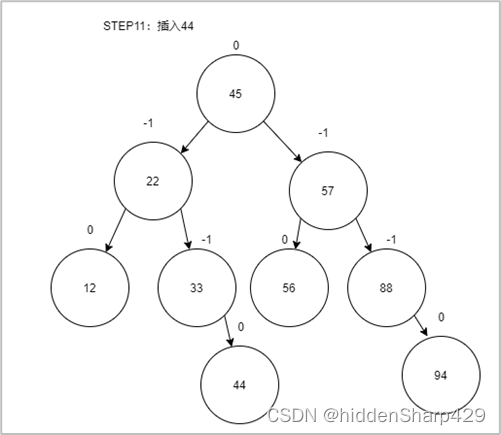
在这里插入图片描述

第十二步：插入11

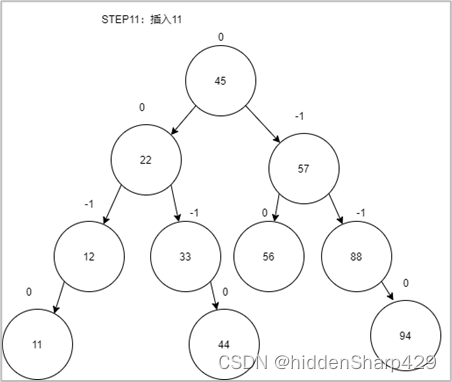
在这里插入图片描述

3. 设哈希函数 $H (K) = 3 K m o d 11$ ，哈希地址空间为0～10，对关键字序列32，13，49，24，38，21，4，12，按下述两种解决冲突的方法构造哈希表，并分别求出等概率下查找成功时和查找失败时的平均查找长度 $A S L s u cc$ 和 $A S Lu n s u cc$

线性探测法
链地址法

解答

第一步：带入 $H (K)$ 中计算

将32，13，49，24，38，21，4，12带入 $H (K)$ 中算得
$H (32) = 8 ； H (13) = 6 ； H (49) = 3 ； H (24) = 6 ； H (38) = 9 ； H (21) = 8 ； H (4) = 1 ； H (12) = 9 ；$
易得:38与 12冲突， 13 与24冲突， 21与 32冲突

第二步：使用线性探测法和链地址法来解决冲突并构建哈希表

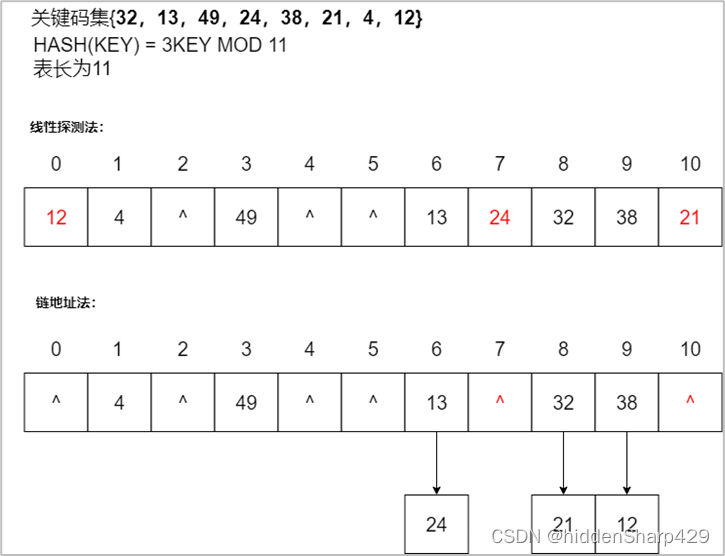
在这里插入图片描述

第三步：计算查找成功时和查找失败时的平均查找长度 $A S L s u cc$ 和 $A S Lu n s u cc$

线性探测法装填因子 $α = 8/11$ ：
- $ASLsucc=\frac{1}{2}(1+\frac{1}{1-\alpha}) = 2.33$
- $ASLunsucc=\frac{1}{2}(1+\frac{1}{(1-\alpha)^2}) =7.224$
链地址法装填因子 $α = 5/11$ ：
- $\frac{a}{2}=1.227$
- $ASLunsucc=\alpha+e^a=1.482$

4. 假设一棵平衡二叉树的每个结点都标明了平衡因子b，设计一个算法，求平衡二叉树的高度。

本来想把整个平衡二叉树排序流程都给实现的，但是在旋转结点的时候出现了问题并且找不到方法解决（指针的指针都解决不了），故这题并不是一个完整的可执行程序

核心思想

求高度的方法：
从根节点开始，每个结点的bf值若为1则左边的树深度更深，为-1则右边的树深度更深，为0则两边一样深度，只需要一直往深的一边前进，直到为空停止即可。

核心函数

// 求平衡二叉树的高度代码
int AvlTreeHeight(AvlTree root)
{
    int height = 0;
    if (root->left == nullptr && root->right == nullptr) // 或root->bf == 0也行
    {
        return 1; // 若只有根节点则返回高度为1
    }

    while (root != nullptr) // 一直为空才停止
    {
        if (root->bf == 1 && root->bf == 0)
        {
            root = root->left;
            height++;
        }
        else
        {
            root = root->right;
            height++;
        }
    }
    return height;
}