题目

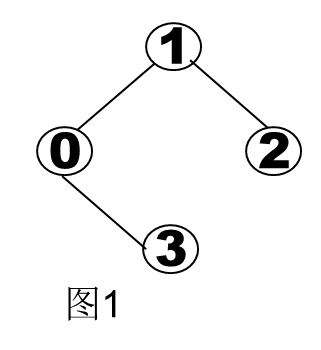
  Qestion: 设计一个算法,判断一个未知顶点个数和边数的无向连通图G是否是棵树,假设图采用邻接表存储。若是树,返回true;否则返回 false。
(用图1和图2验证作业题2算法的正确性)

---

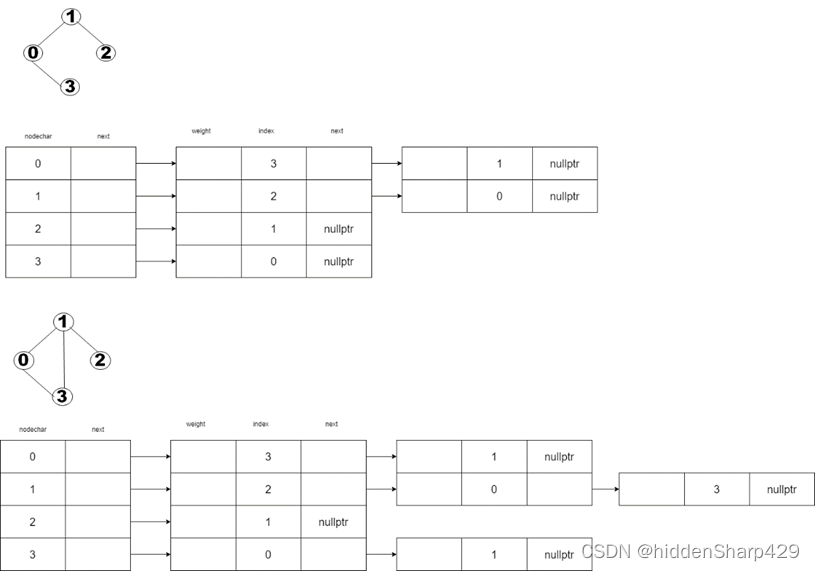
图一图二的邻接表结构

---

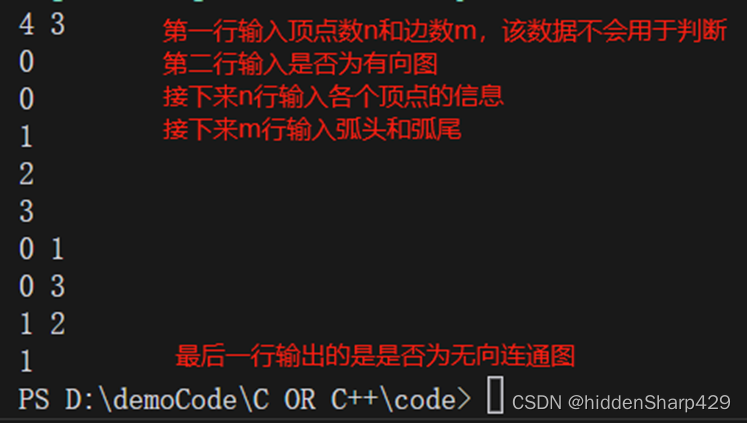
运行结果以及其解释

由结果可知图一为无向连通图，图二不为无向连通图

图一的运行结果

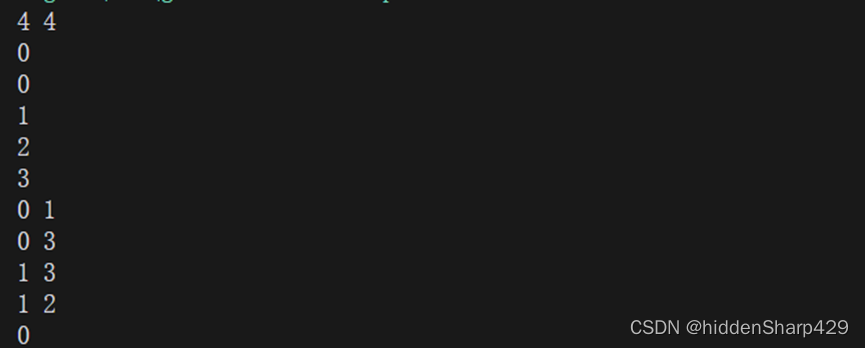
图二的运行结果

---

数据结构与定义

#include <stdio.h>
#include <iostream>

using namespace std;

#define MaxSize 20 // 最大顶点的个数
struct Node
{
    int weight;
    int index;
    struct Node *next;
};
struct HNode
{
    char nodeData;
    struct Node *next;
};
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    HNode verList[MaxSize];
};

---

主控函数

bool IsTree(Graph G){ }

bool IsTree(Graph G)
{
    bool IsVisited[MaxSize]; // 记录每个顶点是否被访问过
    int NodeCnt = 0;         // 记录访问的顶点个数
    int ArcCnt = 0;          // 记录边的个数
    bool IsTree = false;     // 判断图G是否为树
    DFS(G, G.verList[0], 0, IsVisited, NodeCnt, ArcCnt);
    if ((!G.isDireted) && (ArcCnt / 2 == NodeCnt - 1)) // 因为是无向图所以边要除以2
    {
        IsTree = true; // 无向连通图G中恰好有n-1条边
    }
    return IsTree;
}

---

核心函数

void DFS(Graph G, HNode V, int i, bool IsVisited[], int &NodeCnt, int &ArcCnt){ }

void DFS(Graph G, HNode V, int i, bool IsVisited[], int &NodeCnt, int &ArcCnt)
{
    if (!IsVisited[i])
    {
        IsVisited[i] = true;
        NodeCnt++;
        Node *tmp = V.next; // tmp指向HNode的第一个Node结点
        if (tmp == nullptr) // HNode的next为空
        {
            DFS(G, G.verList[i + 1], i + 1, IsVisited, NodeCnt, ArcCnt);
        }
        else // HNode的next不为空
        {
            do
            {
                if (IsArcExist(G.verList[i].nodeData, G.verList[tmp->index].nodeData, G)) // 判断是否有该边长
                {
                    ArcCnt++;
                }
                DFS(G, G.verList[tmp->index], tmp->index, IsVisited, NodeCnt, ArcCnt); // 递归到下一层
                tmp = tmp->next;                                                       // tmp向后移
            } while (tmp != nullptr);                                                  // 当tmp不为nullptr时一直进行DFS并且tmp后移
        }
    }
}

---

完整代码

#include <stdio.h>
#include <iostream>

using namespace std;

#define MaxSize 20 // 最大顶点的个数
struct Node
{
    int weight;
    int index;
    struct Node *next;
};
struct HNode
{
    char nodeData;
    struct Node *next;
};
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    HNode verList[MaxSize];
};

int Locate(char c, Graph G)
{
    int index = -1;
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.verList[i].nodeData == c)
        {
            index = i;
        }
    }
    return index;
}

void InsertVex(Graph &G, char v)
{
    G.verList[G.vertexNum].nodeData = v;
    G.verList[G.vertexNum].next = nullptr;
    G.vertexNum++;
}

void InsertArc(Graph &G, char tail, char head)
{
    int TailIndex, HeadIndex;
    TailIndex = Locate(tail, G);
    HeadIndex = Locate(head, G);
    if (HeadIndex == -1 || TailIndex == -1) // 输入的弧头或者弧尾不存在
    {
        return;
    }
    // 无论G为有向图还是无向图
    Node *newNode = new Node;
    newNode->next = G.verList[TailIndex].next; // 头插法插入到邻接表中
    newNode->index = HeadIndex;
    G.verList[TailIndex].next = newNode;
    if (!G.isDireted) // G为无向图
    {
        Node *newNode = new Node;
        newNode->next = G.verList[HeadIndex].next; // 头插法插入到邻接表中
        newNode->index = TailIndex;
        G.verList[HeadIndex].next = newNode;
    }
}

void CreateGraph(Graph &G)
{
    cin >> G.vertexNum >> G.arcNum; // 输入顶点数和边数
    cin >> G.isDireted;             // 输入是否为有向图
    if (G.vertexNum > MaxSize)
    {
        return;
    }
    // 初始化顶点列表
    for (int i = 0; i < G.vertexNum; i++)
    {
        cin >> G.verList[i].nodeData;
        G.verList[i].next = nullptr;
    }
    // 依次输入各边的信息
    for (int j = 0; j < G.arcNum; j++)
    {
        char ArcHead, ArcTail;
        cin >> ArcTail >> ArcHead;
        InsertArc(G, ArcTail, ArcHead);
    }
}

bool IsArcExist(char a, char b, Graph G)
{
    int AIndex, BIndex; // 找到弧头和弧尾的数组下标
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.verList[i].nodeData == a)
        {
            AIndex = i;
            continue;
        }
        if (G.verList[i].nodeData == b)
        {
            BIndex = i;
            continue;
        }
    }
    Node *tmp = G.verList[AIndex].next;
    while (tmp != nullptr)
    {
        if (tmp->index == BIndex)
        {
            return true;
        }
        tmp = tmp->next;
    }
    return false;
}

void DFS(Graph G, HNode V, int i, bool IsVisited[], int &NodeCnt, int &ArcCnt)
{
    if (!IsVisited[i])
    {
        IsVisited[i] = true;
        NodeCnt++;
        Node *tmp = V.next; // tmp指向HNode的第一个Node结点
        if (tmp == nullptr) // HNode的next为空
        {
            DFS(G, G.verList[i + 1], i + 1, IsVisited, NodeCnt, ArcCnt);
        }
        else // HNode的next不为空
        {
            do
            {
                if (IsArcExist(G.verList[i].nodeData, G.verList[tmp->index].nodeData, G)) // 判断是否有该边长
                {
                    ArcCnt++;
                }
                DFS(G, G.verList[tmp->index], tmp->index, IsVisited, NodeCnt, ArcCnt); // 递归到下一层
                tmp = tmp->next;                                                       // tmp向后移
            } while (tmp != nullptr);                                                  // 当tmp不为nullptr时一直进行DFS并且tmp后移
        }
    }
}

bool IsTree(Graph G)
{
    bool IsVisited[MaxSize]; // 记录每个顶点是否被访问过
    int NodeCnt = 0;         // 记录访问的顶点个数
    int ArcCnt = 0;          // 记录边的个数
    bool IsTree = false;     // 判断图G是否为树
    DFS(G, G.verList[0], 0, IsVisited, NodeCnt, ArcCnt);
    if ((!G.isDireted) && (ArcCnt / 2 == NodeCnt - 1)) // 因为是无向图所以边要除以2
    {
        IsTree = true; // 无向连通图G中恰好有n-1条边
    }
    return IsTree;
}

int main()
{
    Graph G;
    CreateGraph(G);
    bool res = IsTree(G);
    cout << res << endl;
    return 0;
}

---

结束语

  因为是算法小菜，所以提供的方法和思路可能不是很好，请多多包涵~如果有疑问欢迎大家留言讨论，你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗？我们之间的交流是我最大的动力！