leetcode:移动零

news2024/10/6 2:20:35

移动零

easy

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:

1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1

**进阶：**你能尽量减少完成的操作次数吗？

法1：操作次数多，效率非常低

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        for i, num in enumerate(nums):
            
            if num == 0:
                nums.remove(0)
                nums.append(0)
                
        return nums

法2：双指针（效率高）

演示：

步骤一：

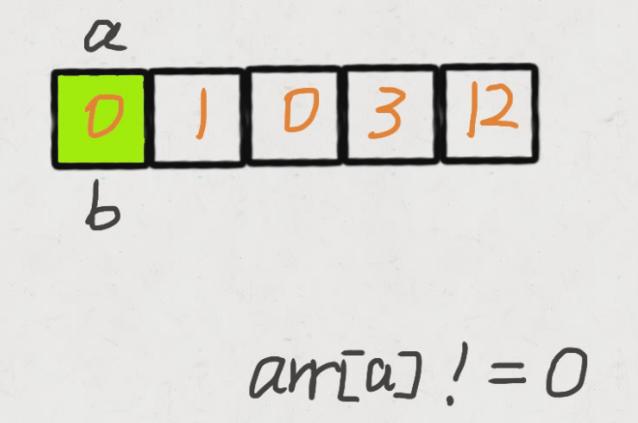
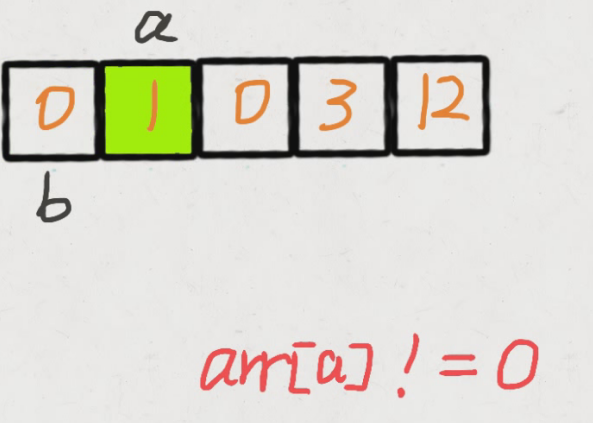
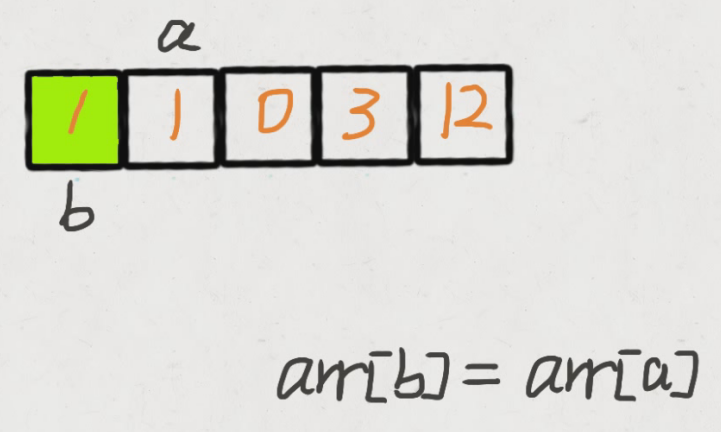
步骤二

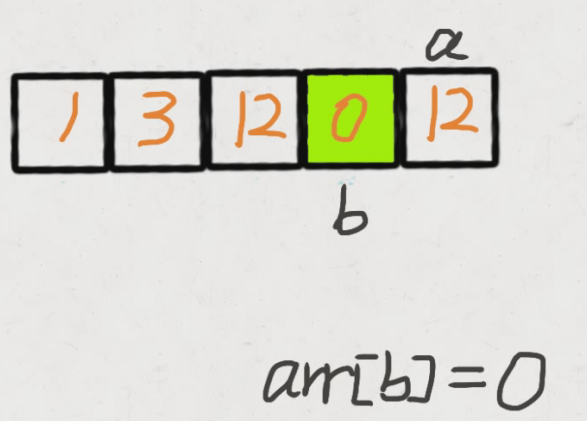
class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = j = 0#设置双指针
        
        #步骤一
#i遍历数组，j指向为0的下标，当nums[i]不为0时，将nums[i]的值替换到nums[j]，然后j向后移动一位
        while i < len(nums):
            if nums[i] != 0:
                nums[j] = nums[i]
                j += 1
            i += 1
		#步骤二
#步骤一已经将所有非0数移到前面去了，现在j在最后一个非0数之后，将j到结尾的数全部赋值为0
        while j < len(nums):
            nums[j] = 0 
            j += 1
        
        return nums