所谓的AVL树也叫做高度平衡的二叉搜索树。
啥是高度平衡的二叉搜索树？
高度平衡的二叉搜索树：意味着左右子树的高度最大不超过一。
我们先来回顾一下二叉搜索树的概念：
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
- 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
它或许是个完全二叉树：
在极端情况下又是个单分支的树：
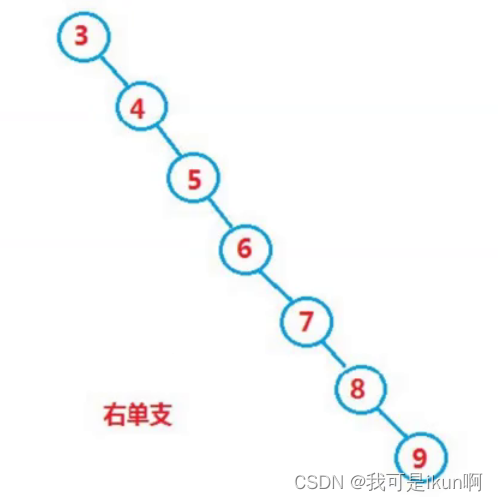
一个二叉搜索树的时间复杂度为：O(N), 极端情况下，例如上图（左右单支）的情况，树的高度很高，那么就会导致搜索的效率很低，如果此时有N个树，树的高度就为N。
所以我们需要一颗更高效的树，这就是高度平衡的二叉搜索树，这也就是为什么需要高度平衡的原因。
AVL树的概念
二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如图：
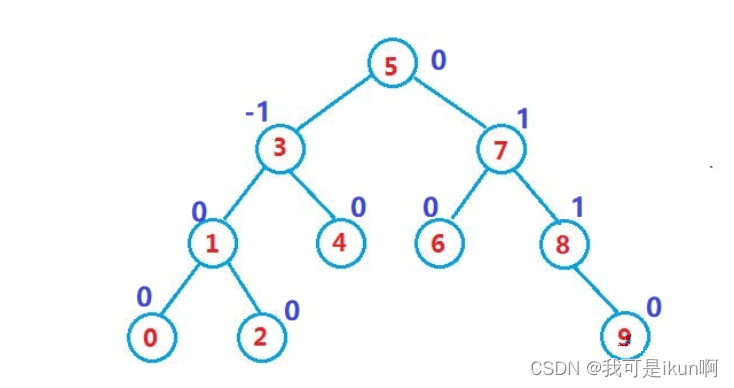
每个结点旁的数字代表着其平衡高度，左子树存在一个为 -1，右子树存在一个即为1，不存在则为0。
其中，3 结点上，左子树的高度为2，所以左子树的平衡因子应该为 -2，右子树的高度为1，所以右子树的平衡因子为1，二者相结合的平衡因子应该为：-1。
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 O( logN)，搜索时间复杂度O( logN)。
实现AVL树的相关代码
AVL树节点的定义
AVL树结点的定义其实很简单：
static class TreeNode {
public TreeNode left; // 节点的左孩子
public TreeNode right; // 节点的右孩子
public TreeNode parent ; // 节点的双亲
public int val = 0;
public int bf = 0; // 当前节点的平衡因子=右子树高度-左子树的高度
public TreeNode(int val) {
this.val = val;
}
}
注意：
当前节点的平衡因子=右子树高度-左子树的高度。但是，不是每棵树，都必须有平衡因子，这只是其中的一种实现方式。
AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：
- 按照二叉搜索树的方式插入新结点
- 调节结点的平衡因子
这里我们画图一步步来讲解。
我们先来随便画棵树：
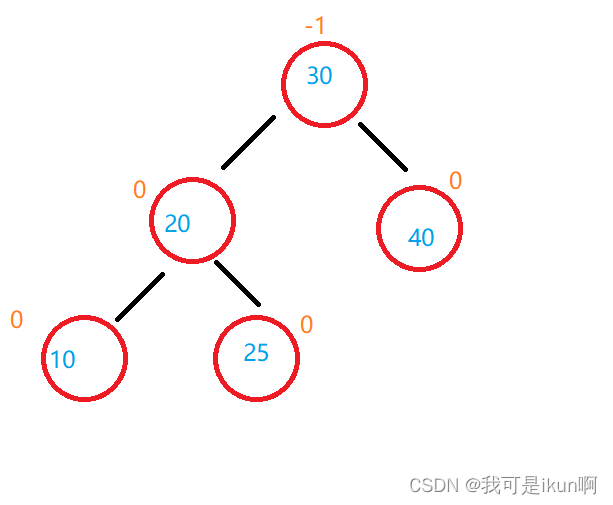
现在我们有这样一棵AVL树，我们给它插入一个 5 的结点。
还是和二叉搜索树一样去寻找，从根节点开始，大于根结点的值向右走，小于根节点的向左走，以此类推。
此时，我们需要重新调节平衡因子：
此时就需要对整棵树进行一个旋转。
树的旋转
右单旋
既然它不平衡，那就需要想办法让他平衡。
这里只是其中一种旋转，我们再来看看其他情况：
左单旋
我们现在有这样一棵树：
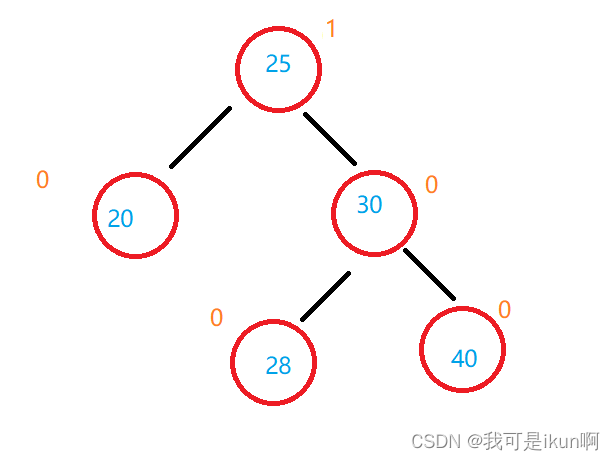
我们新插入一个50：
此时，25 的结点就不平衡了，我们也需要旋转：
旋转过后：
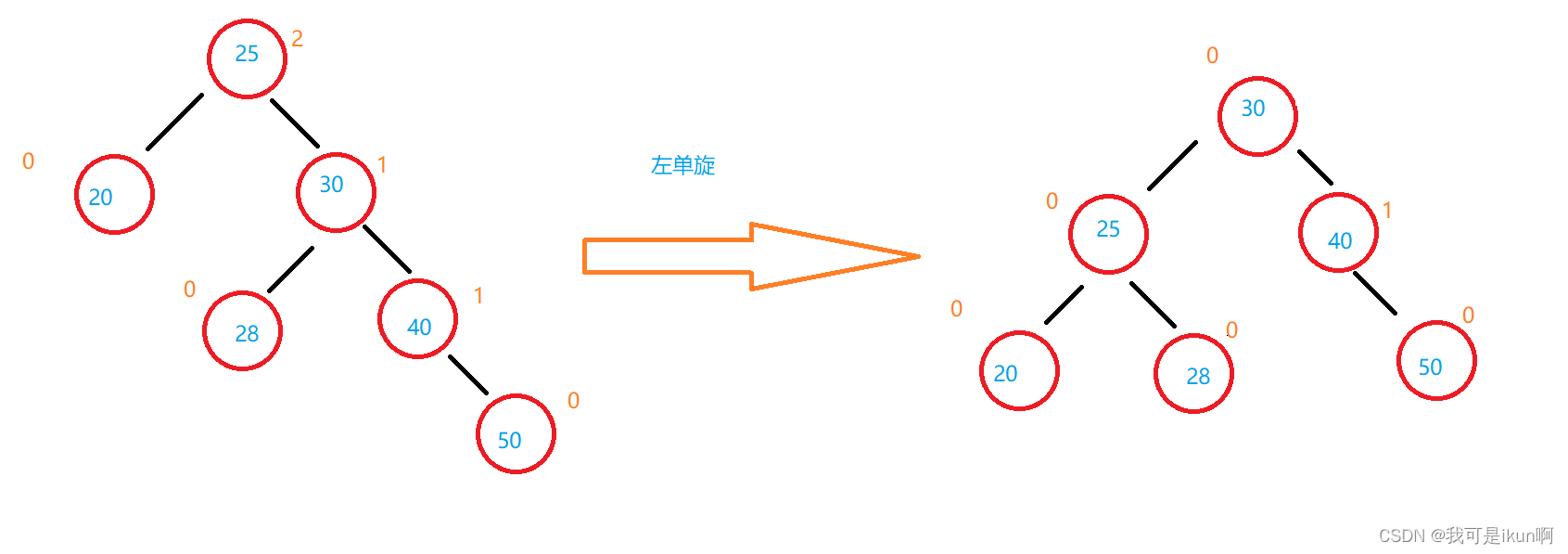由上述的两种旋转我们看到一个细节：
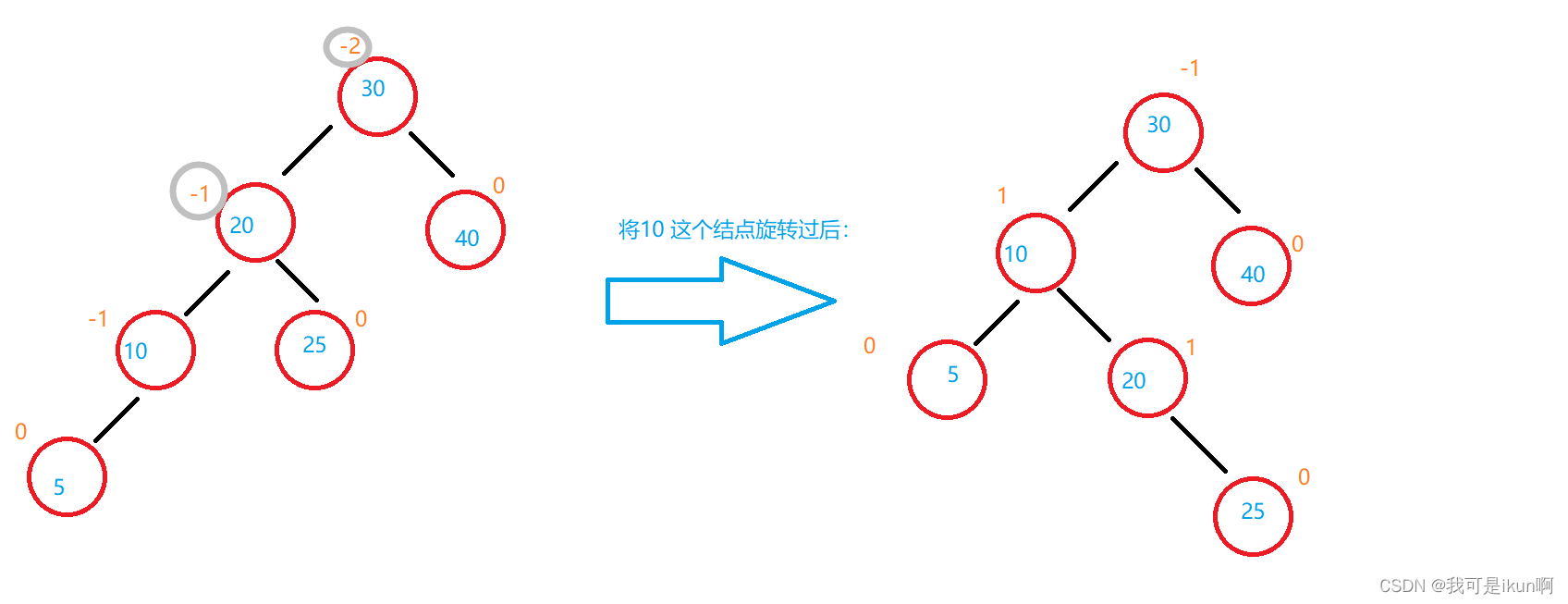
- 不平衡时，该不平衡的结点和其子节点的平衡因子必然同号，此时我们只需要单旋即可。
- 并且，平衡因子为负数需要发送右旋，平衡因子为正数需要发生左旋
- 如若，异号则需要发生双旋
左右双旋
我们还是以发生右单旋的图为基础，我们现在不插入5，而是插入 28 ；
如图：
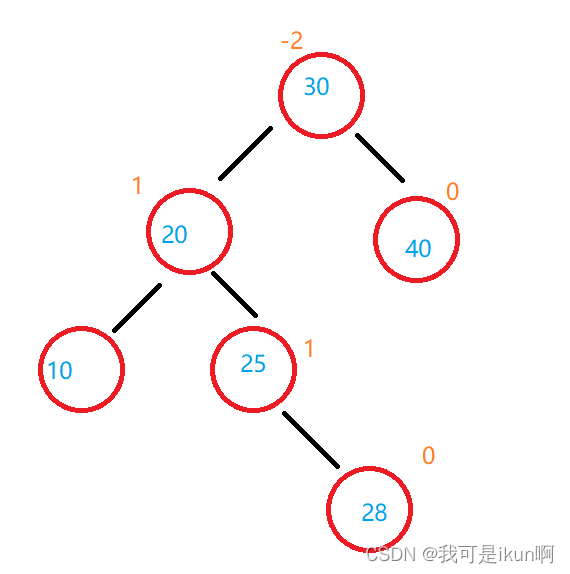
我们可以看出来：30 这个节点上的平衡因子和 20 这个节点上的平衡因子异号了。
无论是左单旋还是右单旋都无济于事。不信可以自己去画画图；
最终结果如图所示：
右左双旋
我们在左单旋的基础上，插入一个值为 26 的结点，如下图：
同样的，无法用单旋来解决问题。
我们需要先右单旋在左单旋；如下图：
ok，上面只是介绍了单旋是怎么旋转的，接下来要开始讲解代码了。
代码实现
插入方法代码
首先，我们要将这个方法设置为布尔值类型，因为这个方法是有可能无法执行的。
AVL树是基于二叉搜索树衍生的，二叉搜索树中是无法实现插入相同的值。
所以这里的插入方法可以参考参考二叉搜索树。
第一步，需要判断根节点是否为空，为空那么这个需要插入的 val 就直接为根结点就行了。
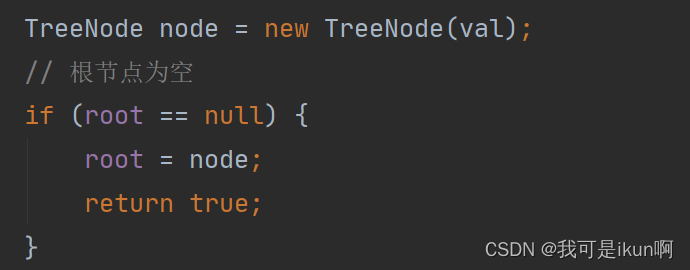
第二步，开始遍历，设置 一个 cur ，一个 parent ，两个TreeNode ，去找目标 val 应该要插入的位置。
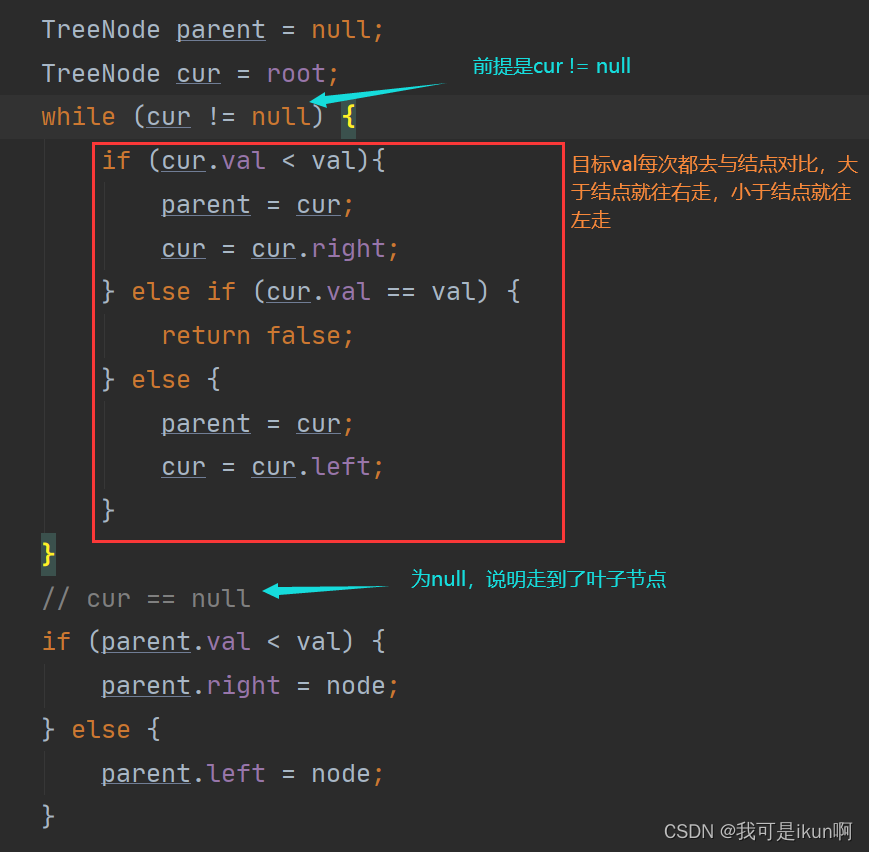
ok，目前为止与二叉搜索树没有太大差别，我们到这里已经找到了目标 val 应该插入的为止，还需要解决 平衡因子和转换后各个结点的关系。
此时的 node 已经是叶子节点了
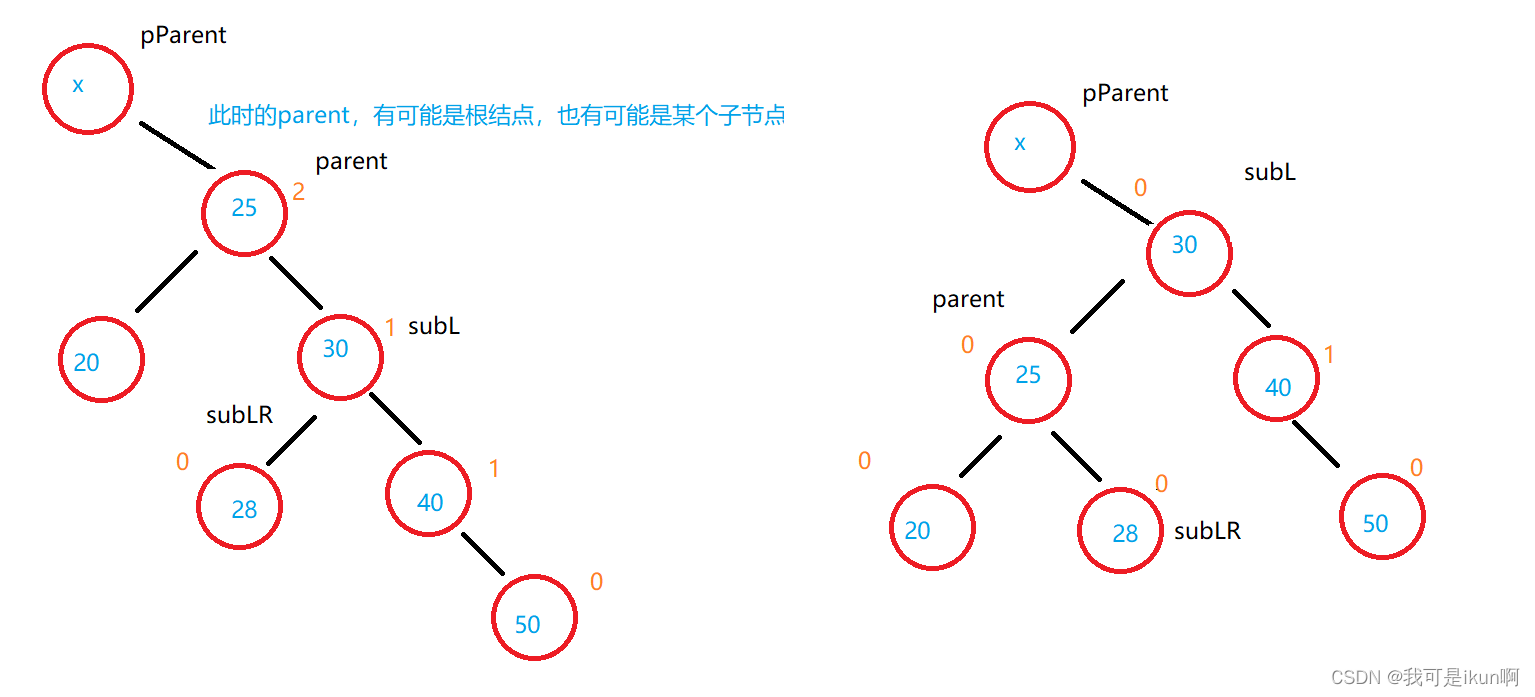
为啥这里的循环条件是parent != null，我们来看张旋转图：
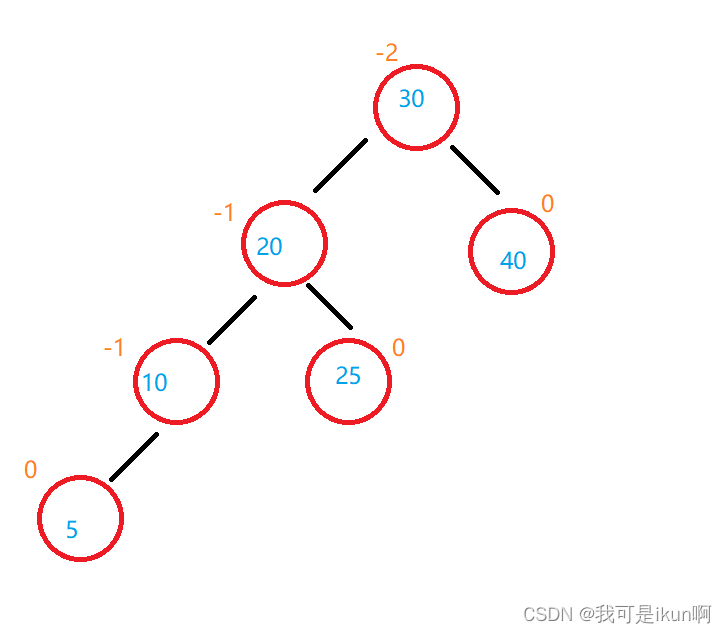
我们图中，30 是个根节点吗？
它也可以是某个结点的子节点（故此，我们还需要向上平衡）；直到调节到根结点才算调整完毕。
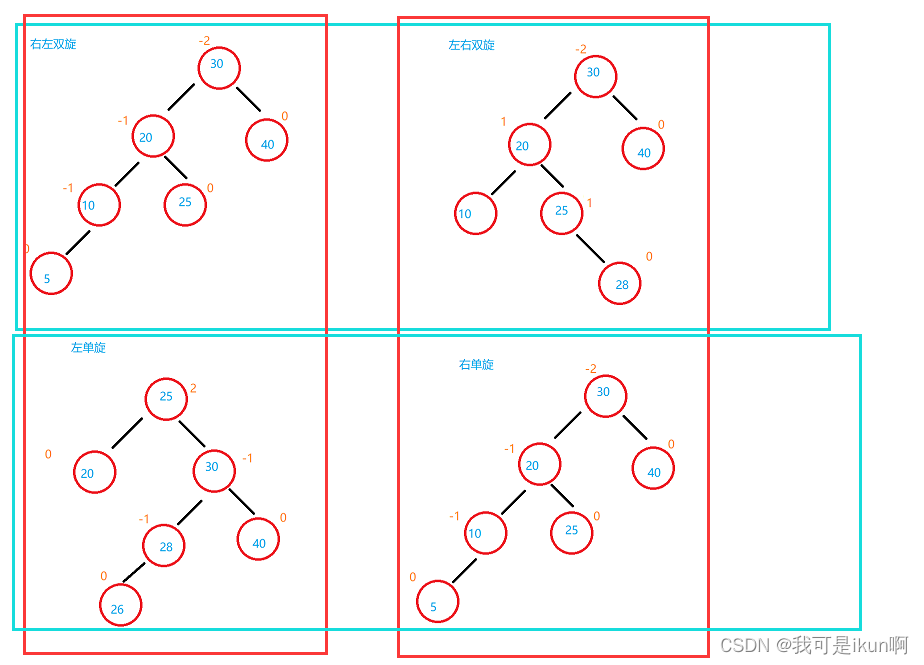
两两对比，就能总结出规律了。
public boolean insert(int val) {
TreeNode node = new TreeNode(val);
// 根节点为空
if (root == null) {
root = node;
return true;
}
TreeNode parent = null;
TreeNode cur = root;
while (cur != null) {
if (cur.val < val){
parent = cur;
cur = cur.right;
} else if (cur.val == val) {
return false;
} else {
parent = cur;
cur = cur.left;
}
}
// cur == null
if (parent.val < val) {
parent.right = node;
} else {
parent.left = node;
}
// 当前只是解决了 left 和 right ，还没有处理 node 的 parent
node.parent = parent;
cur = node;
// 调节平衡因子
while (parent != null) {
// 先看 cur 是 parent 的左还是右；此时决定了平衡因子是 ++ 还是 --
if (cur == parent.right) {
parent.bf++;
} else{
parent.bf--;
}
//检查当前平衡因子是否绝对值 <= 1
if (parent.bf == 0) {
// 记住一个结论: cur 的 parent 的平衡因子为 0 ，
// 那么它插入一个结点一定平衡，此时无论插入右子树还是右子树都无所谓，就不用往上继续调节
// 此时已经平衡了
break;
} else if (parent.bf == 1 || parent.bf == -1) {
// 此时插入一个结点，其父节点未必平衡，需要继续向上调节
cur = parent;
parent = parent.parent;
} else {
if (parent.bf == 2) {
// 此时说明右树高，需要先左旋，再右旋
if (cur.bf == 1) {
rotateLeft(parent);
} else {
// cur.bf == -1
rotateRL(parent);
}
} else {
// cur.bf == -2 ;左树高，需要降低左树的高度
// 同样也分平衡因子为 1 和 -1 两种情况
if (cur.bf == -1) {
// 右旋
rotateRight(parent);
} else {
// cur.bf == 1
rotateLR(parent);
}
}
break;
}
}
return true;
}右单旋
还是需要借助上述的案例来进行讲解：
/**
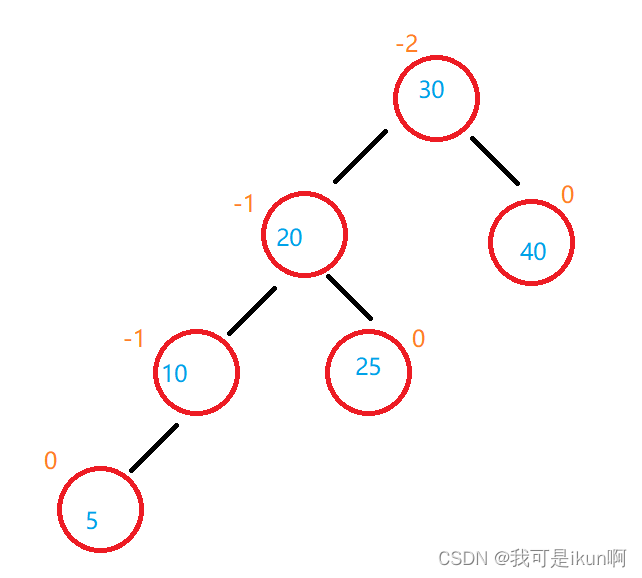
* 右单旋
* @param parent
*/
private void rotateLeft(TreeNode parent) {
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
// 旋转关系 (需要画图)
parent.right = subRL;
subR.left = parent;
if (subRL != null) { // subRL 可能为空
subRL.parent = parent;
}
// 与左单旋一样，需要判断parent 所在的位置是根节点还是某个子树
TreeNode pParent = parent.parent;
parent.parent = subR;
// 为根节点的情况
if (root == parent) {
root = subR;
root.parent = null;
} else {
// 不为根节点的情况
if (pParent.left == parent) {
pParent.left = subR;
} else {
pParent.right = subR;
}
subR.parent = pParent;
}
// 调节平衡因子
subR.bf = parent.bf = 0;
}这里的parent 是需要插入的叶子结点的父节点。
我们首先需要保存一下需要调整位置的几个结点：
第一步：先断开parent 和 subR 之间的关系，建立subRL 和 parent 之间的关系：
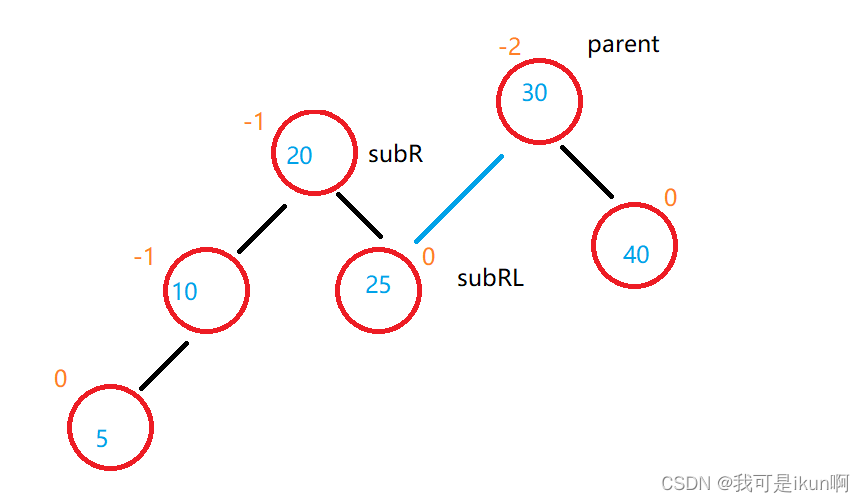
第二步：断开subR 和 subRL 之间的关系，建立subR 和 parent 之间的关系：
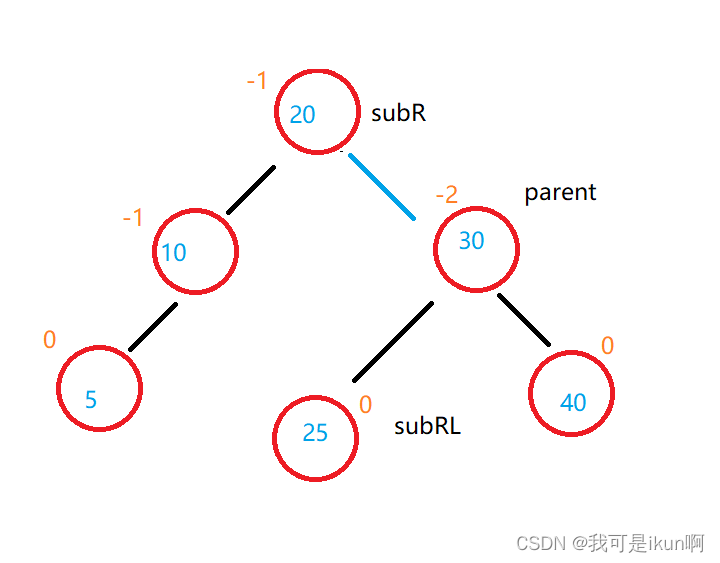
当然啦，subRL并非一定存在，它也可以不存在啊，不存在的情况需要特殊处理一下：
当然，我们目前只确定了彼此之间的left 和 right ，别忘了我们TreeNode 还定义了 parent，所以目前我们还需要处理一下父节点的问题。
如上图，我们需要确定parent 这个结点的位置是否为 根节点，如果是根结点那么 subR 的父节点就是null，如果不是则需要确定具体是 pParent 哪边：
ok，这里就是右单旋的代码，接下来看看左单旋；
左单旋
具体代码：
/**
* 左单旋
* @param parent
*/
private void rotateRight(TreeNode parent) {
// 处理旋转之后几个节点的关系
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
// subLR 是可能为空的，为空还进行就会报错！
if (subLR != null) {
subLR.parent = parent;
}
// 必须先记录父节点的父节点（这一段画图理解）
TreeNode pParent = parent.parent;
parent.parent = subL;
// 判断 parent 是否为 根节点
if(parent == root) {
root = subL;
root.parent = null;
} else {
// 不是根结点，就判断这棵树是左子树还是右子树
if (pParent.left == parent) {
pParent.left = subL;
} else {
pParent.right = subL;
}
}
// 全部调整完毕，还需要调节 平衡因子
subL.bf = 0;
parent.bf = 0;
}同样的，我们得先保存几个需要调整位置的结点，如下图：
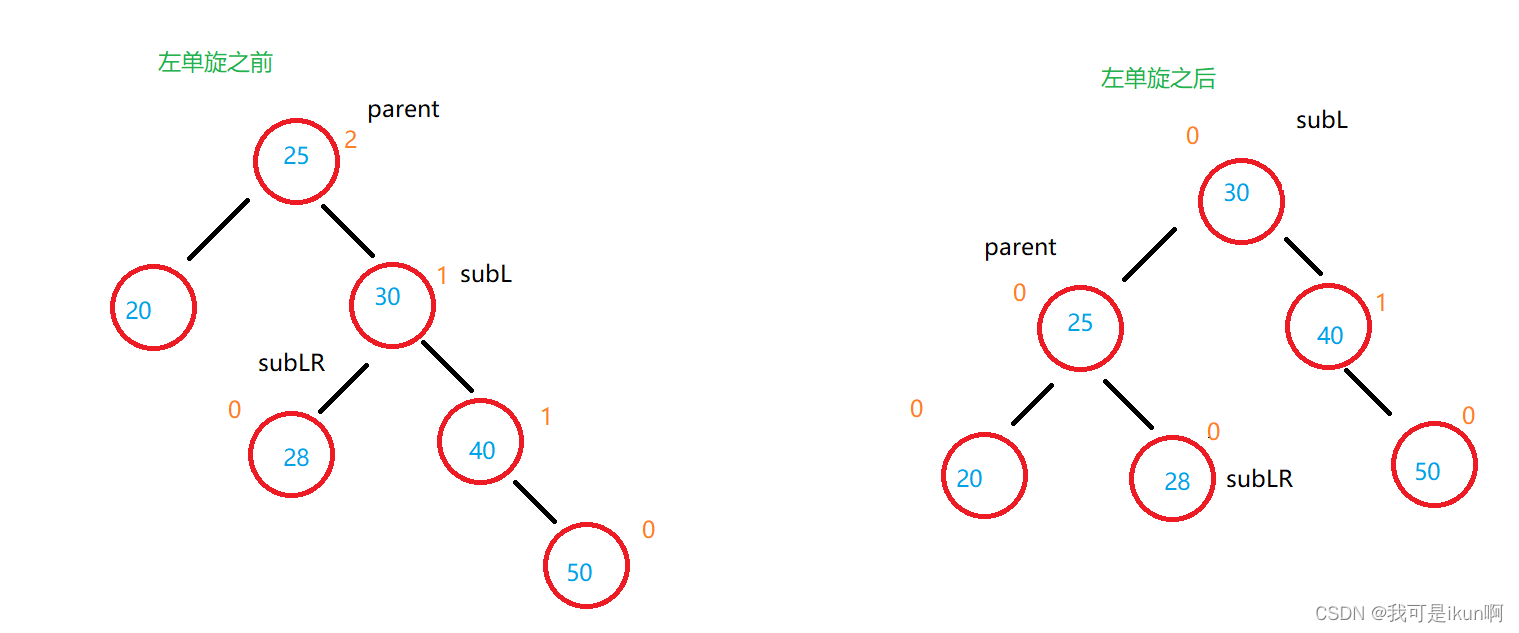
我们先调整 几个结点之间的left 和 right 的关系；
第一步，断开parent 和 subL 之间的关系，连接 parent 和 subLR 的关系：
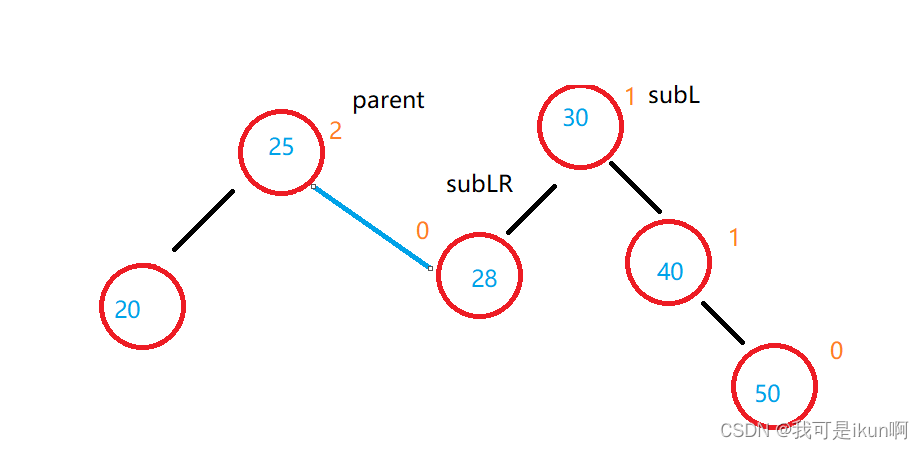
第二步：断开subL 和 subLR 的关系，连接 subL 和 parent 的关系：
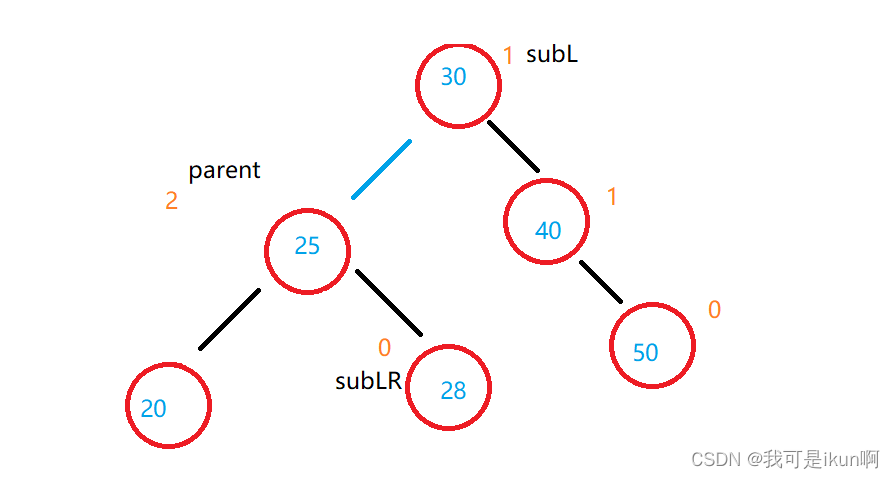
同样的，subLR并非一定存在，它也可以不存在啊，不存在的情况需要特殊处理一下：
接下来的操作都一样：
右左双旋
确实双旋比单旋难不了多少，双旋是建立在单旋的基础上的，只需要单旋两次即可。
先看示意图：
/**
* 右左双旋
* @param parent
*/
private void rotateLR(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
int bf = subLR.bf;
rotateLeft(parent.left);
rotateRight(parent);
if (bf == -1) {
subL.bf = 0;
subLR.bf = 0;
parent.bf = 1;
} else {
// bf == 1
subL.bf = -1;
subLR.bf = 0;
parent.bf = 0;
}
}
我们来看看这两种情况：
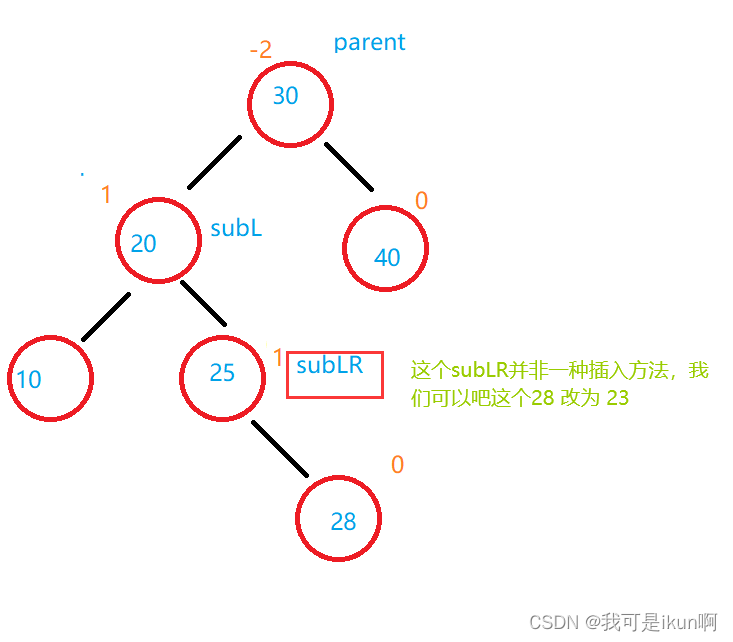
于是就变成了这样：
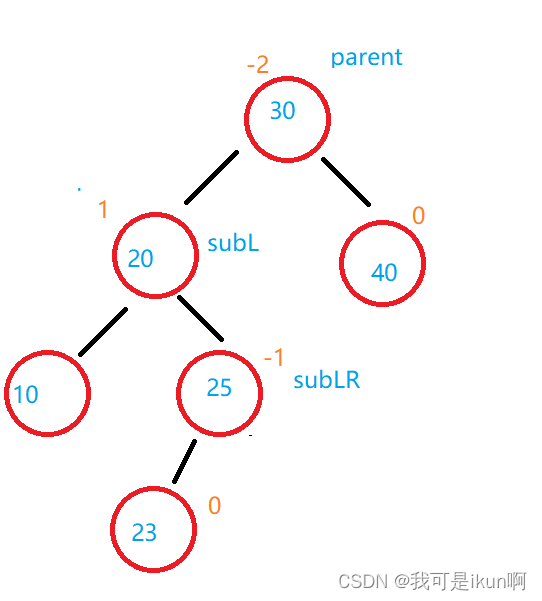
此时的subLR 的平衡因子就是 -1 了，所以需要保留一下sunLR的平衡因子；
旋转还是一样的旋转，只是旋转以后需要改变不同的平衡因子：
同样的， 左右双旋也是同理。
这里就不单独介绍左右双旋，可以自己画个图，然后参考上面右左双旋的做法。
此外还有一个删除没有了解，过后我在此处补齐。
完整代码：
AVLTree/src/AVLTree.java · wjm的码云/Projects - 码云 - 开源中国 (gitee.com)
