回归预测 | MATLAB实现BES-LSSVM秃鹰算法优化最小二乘支持向量机多输入单输出

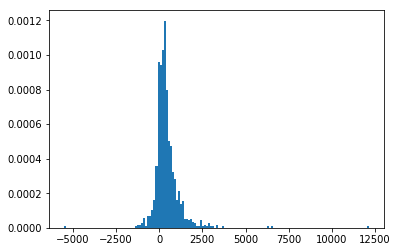
预测效果

基本介绍

MATLAB实现BES-LSSVM秃鹰算法优化最小二乘支持向量机多输入单输出。
MATLAB实现BES-LSSVM秃鹰算法优化最小二乘支持向量机多输入单输出
1.为数据集，输入6个特征，输出一个变量。
2.main.m为主程序主文件，其余为函数文件无需运行。
3.命令窗口输出MAE、MSE、R2、RMSEP和RPD，可在下载区获取数据和程序内容。
4.秃鹰算法优化最小二乘支持向量机,优化RBF 核函数gam和sig。
注意程序和数据放在一个文件夹，运行环境为Matlab2018及以上.

程序设计

• 完整程序和数据下载方式1(资源处直接下载)：MATLAB实现BES-LSSVM秃鹰算法优化最小二乘支持向量机多输入单输出
• 完整程序和数据下载方式2(订阅《智能学习》专栏，同时获取《智能学习》专栏收录程序4份，数据订阅后私信我获取)：MATLAB实现BES-LSSVM秃鹰算法优化最小二乘支持向量机多输入单输出

function [BestSol Convergence_curve timep]=BES(nPop,MaxIt,low,high,dim,fobj)
%nPop: size of population 
%MaxIt:number of iterations 
%low, high : space of Decision variables
%dim : number of Decision variables
%fobj : funcation 
 % paper citation : Alsattar, H. A., Zaidan, A. A., & Zaidan, B. B. (2020). Novel meta-heuristic bald eagle search optimisation algorithm. Artificial Intelligence Review, 53(3), 2237-2264.?
st=cputime;
% Initialize Best Solution
BestSol.cost = inf;
for i=1:nPop
    pop.pos(i,:) = low+(high-low).*rand(1,dim);
     pop.cost(i)=fobj(pop.pos(i,:));
    if pop.cost(i) < BestSol.cost
        BestSol.pos = pop.pos(i,:);
        BestSol.cost = pop.cost(i);
    end
end
 disp(num2str([0 BestSol.cost]))
for t=1:MaxIt
    %%               1- select_space 
    [pop BestSol s1(t)]=select_space(fobj,pop,nPop,BestSol,low,high,dim);
    %%                2- search in space
    [pop BestSol s2(t)]=search_space(fobj,pop,BestSol,nPop,low,high);
    %%                3- swoop
  [pop BestSol s3(t)]=swoop(fobj,pop,BestSol,nPop,low,high);
        Convergence_curve(t)=BestSol.cost;
        disp(num2str([t BestSol.cost]))
    ed=cputime;
    timep=ed-st;
end
function [pop BestSol s1]=select_space(fobj,pop,npop,BestSol,low,high,dim)
Mean=mean(pop.pos);
% Empty Structure for Individuals
empty_individual.pos = [];
empty_individual.cost = [];
lm= 2;
s1=0;
for i=1:npop
    newsol=empty_individual;
    newsol.pos= BestSol.pos+ lm*rand(1,dim).*(Mean - pop.pos(i,:));
    newsol.pos = max(newsol.pos, low);
    newsol.pos = min(newsol.pos, high);
    newsol.cost=fobj(newsol.pos);
    if newsol.cost<pop.cost(i)
       pop.pos(i,:) = newsol.pos;
       pop.cost(i)= newsol.cost;
       s1=s1+1;
         if pop.cost(i) < BestSol.cost
          BestSol.pos= pop.pos(i,:);
         BestSol.cost=pop.cost(i); 
         end
    end
end
function [pop best s1]=search_space(fobj,pop,best,npop,low,high)
Mean=mean(pop.pos);
a=10;
R=1.5;
% Empty Structure for Individuals
empty_individual.pos = [];
empty_individual.cost = [];
s1=0;
for i=1:npop-1
    A=randperm(npop);
pop.pos=pop.pos(A,:);
pop.cost=pop.cost(A);
        [x y]=polr(a,R,npop);
    newsol=empty_individual;
   Step = pop.pos(i,:) - pop.pos(i+1,:);
   Step1=pop.pos(i,:)-Mean;
   newsol.pos = pop.pos(i,:) +y(i)*Step+x(i)*Step1;
    newsol.pos = max(newsol.pos, low);
    newsol.pos = min(newsol.pos, high);
    newsol.cost=fobj(newsol.pos);
    if newsol.cost<pop.cost(i)
       pop.pos(i,:) = newsol.pos;
       pop.cost(i)= newsol.cost;
              s1=s1+1;
                  if pop.cost(i) < best.cost
                 best.pos= pop.pos(i,:);
                best.cost=pop.cost(i); 
            end
    end
end
function [pop best s1]=swoop(fobj,pop,best,npop,low,high)
Mean=mean(pop.pos);
a=10;
R=1.5;
% Empty Structure for Individuals
empty_individual.pos = [];
empty_individual.cost = [];
s1=0;
for i=1:npop
    A=randperm(npop);
pop.pos=pop.pos(A,:);
pop.cost=pop.cost(A);
        [x y]=swoo_p(a,R,npop);
    newsol=empty_individual;
   Step = pop.pos(i,:) - 2*Mean;
   Step1= pop.pos(i,:)-2*best.pos;
   newsol.pos = rand(1,length(Mean)).*best.pos+x(i)*Step+y(i)*Step1;
    newsol.pos = max(newsol.pos, low);
    newsol.pos = min(newsol.pos, high);
    newsol.cost=fobj(newsol.pos);
    if newsol.cost<pop.cost(i)
       pop.pos(i,:) = newsol.pos;
       pop.cost(i)= newsol.cost;
              s1=s1+1;
                  if pop.cost(i) < best.cost
                 best.pos= pop.pos(i,:);
                best.cost=pop.cost(i); 
            end
    end
end
function [xR yR]=swoo_p(a,R,N)
th = a*pi*exp(rand(N,1));
r  =th; %R*rand(N,1);
xR = r.*sinh(th);
yR = r.*cosh(th);
 xR=xR/max(abs(xR));
 yR=yR/max(abs(yR));
 
 function [xR yR]=polr(a,R,N)
%// Set parameters
th = a*pi*rand(N,1);
r  =th+R*rand(N,1);
xR = r.*sin(th);
yR = r.*cos(th);
 xR=xR/max(abs(xR));
 yR=yR/max(abs(yR));

参考资料

[1] https://blog.csdn.net/article/details/126072792?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/article/details/126044265?spm=1001.2014.3001.5502