题目

给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

数据范围: 1≤n,m≤500，矩阵中任意值都满足 0≤ai,j​≤100

要求：时间复杂度O(nm)

例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，

所选择的最小累加和路径如下图所示：

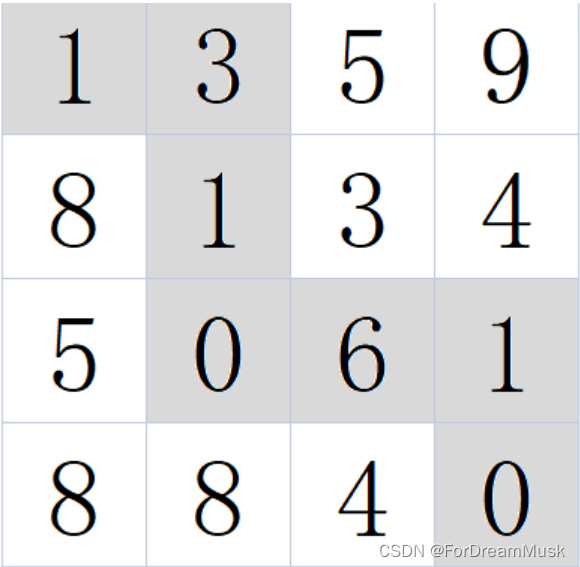
示例1

输入：

[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]

返回值：

12

示例2

输入：

[[1,2,3],[1,2,3]]

返回值：

7

备注：

1≤n,m≤2000

1≤ai,j​≤100

---

代码

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * @param matrix int整型二维数组 the matrix
     * @return int整型
     */
    public int minPathSum (int[][] matrix) {
        //1.创建dp表
        int m = matrix.length, n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 1];

        //2.初始化
        for(int i = 0; i <= m; i ++) {
            dp[i][0] = Integer.MAX_VALUE;
        }
        for(int j = 0; j <= n; j++) {
            dp[0][j] = Integer.MAX_VALUE;
        }
        dp[0][1] = dp[1][0] = 0;

        //3.填表
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j] = Math.min(dp[i- 1][j], dp[i][j - 1]) + matrix[i - 1][j - 1];
            }
        }

        //4.返回值
        return dp[m][n];
    }
}