案例1 高点和高程
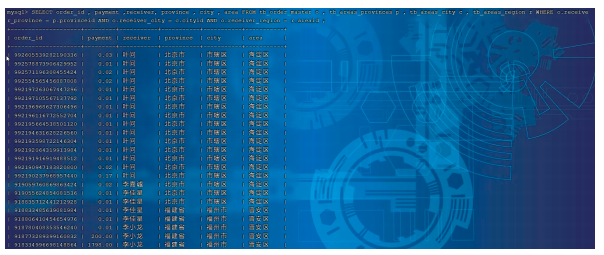
在一丘陵地带测量高程,x和y方向每隔100m测一个点,得到高程如下表所列,试插值一曲面,确定合适的模型,并由此测到最高点和相应的高程。
| x0/z0\y0 | 100 | 200 | 300 | 400 | 500 |
| 100 | 636 | 697 | 624 | 478 | 450 |
| 200 | 698 | 712 | 630 | 478 | 420 |
| 300 | 680 | 674 | 598 | 412 | 400 |
| 400 | 662 | 626 | 552 | 334 | 310 |
【符号设置】
- x0,y0,z0 插值节点的三个维度,取值如上表;
- x,y,z 待插节点三个维度,x,y以10m为间距;
- Xmax,Ymax 表示最高点;
- Zmax 表示最高点高程;
- spline 默认插值方法:三次样条插值
【建立模型】
设地貌函数为z=S(x,y),z为任意点(x,y)处高程,插值要求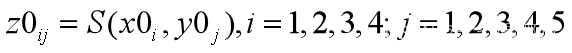
【模型求解】
x0=100:100:400;
y0=100:100:500;
z0=[636 697 624 478 450;698 712 630 478 420;
680 674 598 412 400;662 626 552 334 310];
pp=csape({x0,y0},z0);
x=100:10:400;y=100:10:500;
z=fnval(pp,{x,y});
zmax=max(max(z));
[dx,dy]=find(z==zmax);
[x(dx),y(dy),zmax]
[X,Y]=meshgrid(x,y);
Z=z';
mesh(X,Y,Z);
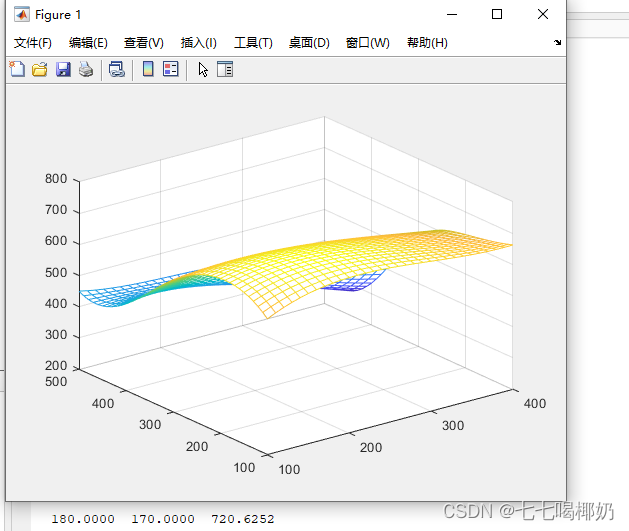
180.0000 170.0000 720.6252
案例2 海底曲面图的绘制
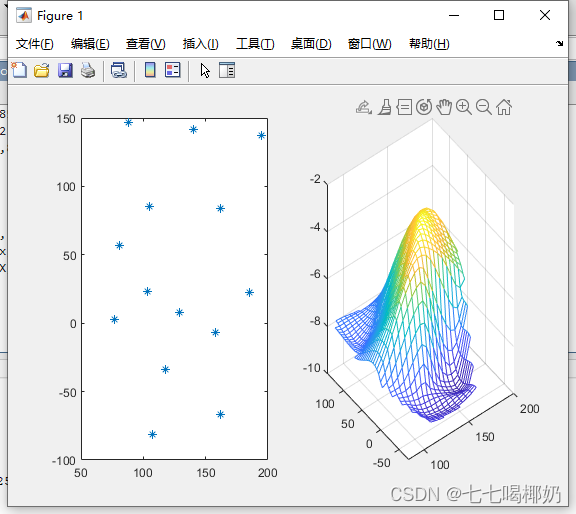
在某海域测得一些点(x,y)处的深度z由下表给出,在适当的矩形区域内绘制海底曲面的图形。
| X | 129 | 140 | 103.5 | 88 | 185.5 | 195 | 105 |
| Y | 7.5 | 141.5 | 23 | 147 | 22.5 | 137.5 | 85.5 |
| z | 4 | 8 | 6 | 8 | 6 | 8 | 8 |
| X | 157.5 | 107.5 | 77 | 81 | 162 | 162 | 117.5 |
| Y | -6.5 | -81 | 3 | 56.5 | -66.5 | 84 | -33.5 |
| z | 9 | 9 | 8 | 8 | 9 | 4 | 9 |
【模型计算】
x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
xmm=minmax(x);
ymm=minmax(y);
X=xmm(1):5:xmm(2);
Y=ymm(1):5:ymm(2);
Z=griddata(x,y,z,X,Y','cubic');
subplot(1,2,1), plot(x,y,'*')
subplot(1,2,2), mesh(X,Y,Z)