给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = “babad” 输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd” 输出：“bb”

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

解题思路：

1.本题 s 的长度最多为10^3, 所以 O(n^2)复杂度的算法是允许的。

2.回文串是具有天然状态转移性质的，一个字符串若是回文字符串（长度大于2）那么去掉两头仍然是回文串。

3.

即dp[ i ][ j ] 表示字符串s下标 i ~ j 是否为回文串是则dp[ i ][ j ] = true,反之false

4.

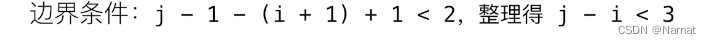
即s的下标（i + 1）~ (j - 1）区间长度小于2，肯定是个回文串，那就没必要继续判断了

5.

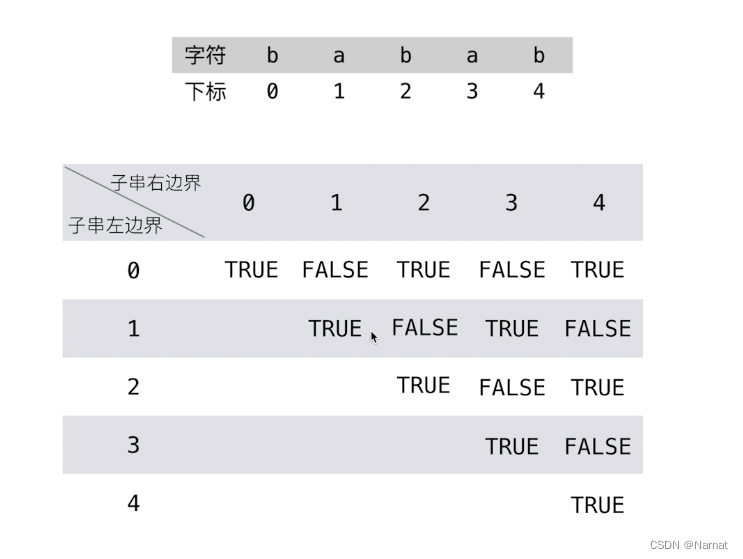
由于dp[i + 1][j - 1] 的位置在dp[i][j]的左下角方位，所以填表方式不能从左往右，而是从上往下

理论成立代码：

class Solution {
    public String longestPalindrome(String s) {
           int len = s.length();
           if(s.length() < 2) return s;//特殊处理
           
           //查找最长字符串
           int maxlen  = 0;
           int begin = 0;
           char stoc[] = s.toCharArray();
           boolean dp[][] = new boolean [len][len];
           //for(int i = 0; i < len; i ++) dp[i][i] = true;//初始化
           
           for(int j = 0; j < len; j ++)//填表格
        	   for(int i = 0; i <= j; i ++) {//从上往下填
        		  
        		   if(stoc[i] != stoc[j]) {//两头不一样，那就不是回文
        			   dp[i][j] = false;
        		   }
        		   else {
        			   if(j - i < 3) dp[i][j] = true;//如果内部字符串长度小于2则为回文
        			   else {
        				   dp[i][j] = dp[i + 1][j - 1];//否则迭代
        			   }
        		   }
        		   
        		   if(dp[i][j] == true && j - i + 1 >= maxlen) {//查找
        			   maxlen = j - i + 1;
        			   begin = i;
        		   }
        		   
        	   } 
           
           return s.substring(begin, begin + maxlen);//左闭右开
    }
}