什么是动态规划

动态规划（dp）是一种通过将问题分解为子问题，并利用已解决的子问题的解来求解原问题的方法。适用于具有重叠子问题和最优子结构性质的优化问题。通过定义状态和状态转移方程，动态规划可以在避免重复计算的同时找到问题的最优解，是一种高效的求解方法，常用于解决各种问题，如最短路径、背包问题、序列比对等。

---

区间dp

定义

区间dp是一种dp的应用，用于解决涉及区间的问题。
它将问题划分为若干个子区间，并通过定义状态和状态转移方程来求解每个子区间的最优解，最终得到整个区间的最优解。

---

应用

区间动态规划常用于解决一些涉及区间操作的问题，如最长公共子序列、最长回文子串等。在区间动态规划中，通常需要定义一个二维数组来表示子区间的状态，并通过填表的方式逐步求解子区间的最优解，最后得到整个区间的最优解。区间动态规划是一种高效的求解方法，可以有效地解决各种区间问题。

---

---

例题引入

石子合并是一道非常经典的区间DP的例题，很适合新手练习，下面我们看看这个题目：

题目描述

在一个圆形操场的四周摆放 $N$ 堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

输入格式

数据的第 $1$ 行是正整数 $N$，表示有 $N$ 堆石子。

第 $2$ 行有 $N$ 个整数，第 $i$ 个整数 $a_i$ 表示第 $i$ 堆石子的个数。

输出格式

输出共 $2$ 行，第 $1$ 行为最小得分，第 $2$ 行为最大得分。

样例

样例输入

4
4 5 9 4

样例输出

43
54

提示

$1\le N\le 100$，$0\le a_i\le 20$。

---

---

贪心法

稍微想想就知道不可行，因为它每次只能合并相邻的两堆石子，用贪心的话会答案错误，因此我们考虑区间dp。

---

区间dp

利用区间动态规划来解决此类问题。

优缺点：

优点	缺点
可以求出正解	时间复杂度高
代码量相对较少	效率低
容易理解	数据量大会超时

确实，此题的时间复杂度高达$O(2n^3)$，若非这道题的数据量极小，下面的代码便会超时，那么就需要用一个特殊方法来优化一下。

AC代码：

#include <bits/stdc++.h>
using namespace std;
int n,ans1=0x7fffffff,ans2,a[300],sum[300];
int mi[300][300],ma[300][300];
int main() {
	cin >>n;
	for (int i=1; i<=n; i++) {
		cin >>a[i];
		a[i+n]=a[i];
	}
	for (int i=1; i<=2*n; i++)
		sum[i]=sum[i-1]+a[i];
	memset(mi,0x3f,sizeof(mi));
	for (int i=1; i<=2*n; i++)
		mi[i][i]=0;
	for (int l=1; l<n; l++) {
		for (int i=1; i+l<=2*n; i++) {
			for (int k=i; k<i+l; k++) {
				mi[i][i+l]=min(mi[i][i+l],mi[i][k]+mi[k+1][i+l]+sum[i+l]-sum[i-1]);
				ma[i][i+l]=max(ma[i][i+l],ma[i][k]+ma[k+1][i+l]+sum[i+l]-sum[i-1]);
			}
		}
	}
	for (int i=1; i<n; i++)
		ans1=min(ans1,mi[i][i+n-1]);
	for (int i=1; i<n; i++)
		ans2=max(ans2,ma[i][i+n-1]);
	cout <<ans1 <<endl <<ans2;
	return 0;
}

代码详解

三层for循环

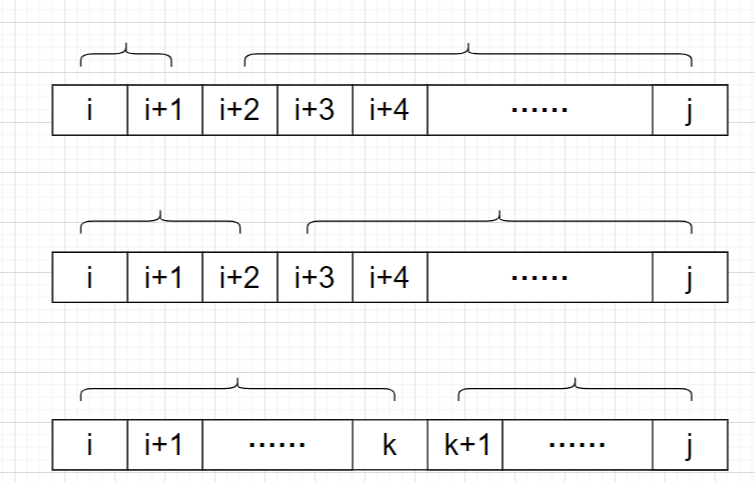
• 第一层for循环用来分区间，我们可以选择将一个大区间分成若干个小区间，那么分的标准是什么呢？这就是第一层for循环的作用，$len$就是每次分的区间长度。
• 第二层循环就是定义区间的左端点，$l=1$，再根据$len=2$，就能确定区间为$(1,2)$，即$f[1][2]$
• 然后第三层循环就是拆分了，如上图，$len=2$的时候是无法拆分了，但是$len=3$的时候是可以拆成$f[1][2],f[3][3],f[1][1],f[2][3]$，以及各个数据都有或没有拆分方法。

状态转移方程

区间拆分了，那么我们如何去算转移方程呢？我们将两个区间 $(1,2)$ 和 $(3,4)$进行合并，那么就是1，2的代价加上3，4的代价，再加上1到4的区间和，具体的式子如下

f[1][4] = min(f[1][4],f[1][2]+f[3][4]+s[4]-s[0]);

为什么这么计算呢，因为你要知道你在求解的过程中是通过小的区间组合成较大的区间的，而你所用到的这两个小的区间$f[1][2]+f[3][4]$，已经得出了最优解了，那么得出最优解需不需要花费代价呢？当然需要，所以我们需要加上那段花费，那么简单来说就是

f[1][2]+f[3][4]=s[2]-s[0]+s[4]-s[2]

因此，状态转移方程便有了：

f[i][i+l]=min(f[i][i+l],f[i][k]+f[k+1][i+l]+s[i+l]-s[i-1]);

环形的处理

我们仔细阅读题目即可发现：石子是按照环形摆放的，因此区间的头和尾是能够合并的，那么如何处理呢？
方法很简单，只需要将整一条线性的石头复制一个，让第二个的头对着第一个的尾，然后正常处理即可。
这一点在程序的很多地方可以体现出来，如：

	for (int i=1; i<=n; i++) {
		cin >>a[i];
		a[i+n]=a[i];
	}

、

	for (int i=1; i<=2*n; i++)

以及

	for (int i=1; i+l<=2*n; i++)

等等。