目录

不定积分

 原函数存在定理：

定理1

定理2：

例题1：

 例题2：

 例题3：

 不定积分的性质：

 不定积分的基本公式：

 例题4：

例题5：

 ​编辑

 例题6：

 三种主要积分法：

 例题7：

 例题8：

 例题9：

 例题10：

 例题11：

 例题12：

 第二类换元法：

 例题13：

 例题14：

例题15：

 ​编辑

 分部积分法：

 例题16：

 例题17：

 例题18：

 例题19：

 例题20：

例题21：

​编辑 

 有理函数积分

例题22：

 ​编辑

 例题23：

 例题24：

三角有理式积分：

 例题25：

 例题26：

 例题27：

 例题28：

 简单无理函数积分

例题29：

 ​编辑

解法2：

 ​编辑

---

不定积分

 原函数存在定理：

定理1

 连续函数一定有原函数。

 证明：连续函数的变上限积分的导数就等于原函数.

定理2：

 有第一类间断点的函数是没有原函数的。

有第二类间断点的函数是可能有原函数的。

例题1：

 

 例题2：

 

 例题3：

 

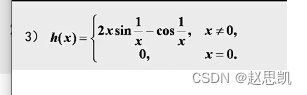
所以有第二类间断点的函数可能有原函数。

 不定积分的性质：

 不定积分的基本公式：

 

 例题4：

 

例题5：

 

 

 例题6：

 

 三种主要积分法：

 

 例题7：

 

 例题8：

 

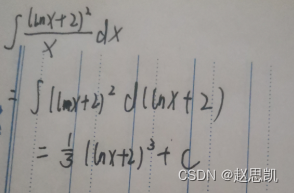
 例题9：

 

 例题10：

 

 例题11：

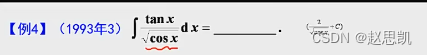
 例题12：

 

 第二类换元法：

 

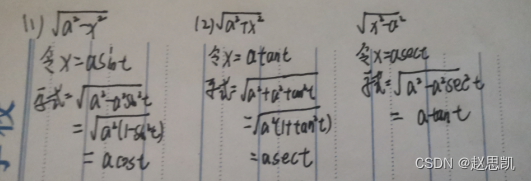
 例题13：

 

 例题14：

例题15：

 

 

 分部积分法：

 

 

 对于分部积分法我们需要知道以下结论：

对于这三个，我们选择把多项式以外的元素凑进去 。

 对于这三个，我们选择把多项式凑近去。

对于这两个，我们需要使用两次分部积分法。

 例题16：

 

 例题17：

 

 例题18：

 

 例题19：

 

 例题20：

 

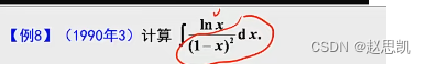
例题21：

 

 

 有理函数积分

例题22：

 

 

 例题23：

 

 例题24：

 

三角有理式积分：

 例题25：

 

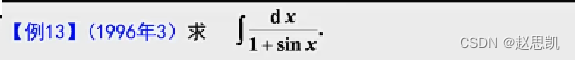
 解法2：

 例题26：

  

 例题27：

 

 例题28：

 

 简单无理函数积分

例题29：

 

 

解法2：