对于时间复杂度，空间复杂度，想必这个是大家在学习数据结构的初级阶段就会第一步认识的吧！！但是，对于复杂度的计算，涉及到了大O渐进法，这个方法是一个笼统的概念，所求得的结果，只是一个大概！并不准确！！希望大家能够了解！！

对于一个算法，我们怎能判断 这个算法是好？？还是坏？？是让我们能看懂？？还是追求什么？？因此下面便引用了复杂度（时间复杂度，空间复杂度）

. 算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作 空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间， 在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计 算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

1.时间复杂度

大O渐进法计算规则

1. 用常数1取代运行时间中的所有加法常数！
2. 在修改后的运行次数函数中，只保留最高项！
3. 如果最高项存在且不是1，则去除与这个项相乘的常数，所得到的结果就是大O阶！

下面笔者用代码加解析的方式，来带领大家走进大O渐进法！！

     //计算func1基本操作了多少次？？
    void func1(int N) {
        int count = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                count++;
            }
        }

        for (int k = 0; k < 2*N; k++) {
            count++;
        }
        
        int M = 10;
        while ((M--) > 0) {
            count++;
        }
    }

对于上述的代码，一共分为三部分！！

1. 第一部分：双重for循环控制的count++;
2. 第二部分:  单层for循环控制的count++;
3. 第三部分:  while循环控制的count++;

 对于上述画图的解析，想必大家都能清楚吧！！ 因此上述代码一共循环：N*N + 2*N + 10次

但是，当随着N的增大……循环的次数也不断增大！！但是，增大的幅度不一样！！

当N = 10 时候：F(N) = 130 

当N = 100 时候： F(N) = 10210

当N = 1000 时候： F(N) = 1002010

因此，随着N的逐渐增大，此时的时间复杂度逐渐趋近于：N*N

因此，上述代码的时间复杂度用大O渐进法来表示就为：O(N^2)

小小练习一下，瞬间开心！！

计算func2的时间复杂度：

    //计算func2的时间复杂度
    void func2(int N) {
        int count = 0;
        for (int k = 0; k < 2*N; k++) {
            count++;
        }
        
        int M =10;
        while ((M--) > 0) {
            count++;
        }
    }

将上述代码进行解析为：

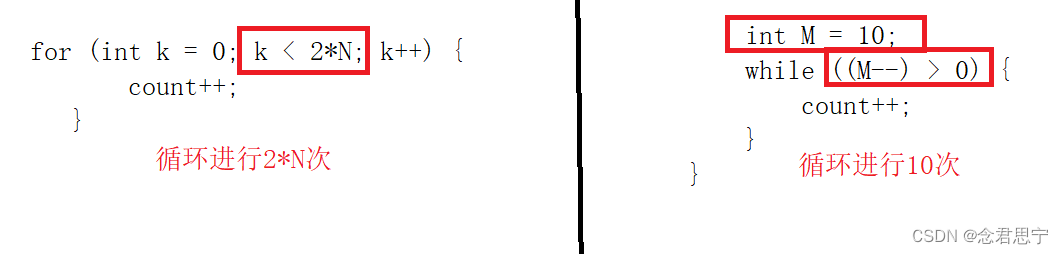
对于上述代码循环进行的总次数为：2*N + 10

因此，用大O渐进法来表示就为：O(N)

为什么将前面的2进行省略，请看笔者开头部分的大O渐进法计算规则：如果最高项存在且不是1，则去除与这个项相乘的常数，

计算func3的时间复杂度：

    //计算func3的时间复杂度：
    void func3 (int N , int M ) {
        int count =0;
        for (int k = 0; k < M; k++) {
            count++;
        }
        for (int k = 0; k < N; k++) {
            count++;
        }
        System.out.println(count);
    }

对于上述的代码，

笔者在刚刚开始用大O渐进法来求时间复杂度的时候，一度以为这个答案会是：O(N)或者O(M)来着，这样想的原因是：当N/M趋近于无穷的时候，那么，复杂度就可以这样想了！！但是，那么疑问又来了：当N/M趋近于无穷的时候，会有栈溢出的现象，从而导致程序崩溃！！所以，这个用大O渐进法来表示时间复杂度为：O(M+N)  请大家好好想一下！！两个未知量M和N，不能省略掉任何一个！！

计算func4的时间复杂度？

   //计算func4的时间复杂度：
    void func4(int N) {
        int count=0;
        for (int i = 0; i < 100; i++) {
            count++;
        }
        System.out.println(count);
    }

对于这个时间复杂度的计算，咋一看代码，还以为是O(N)来着，但是，后来想了想，代码中并没有涉及到N的运算！！虽然，代码执行了100次，但是，仍然是一个常数，既然是一个常数，那么就可以用1来代替！所以，这个代码的时间复杂度为O(1)

 计算bubbleSort的时间复杂度？

  //计算bubbleSort的时间复杂度？
    void bubbleSort(int[] array) {
        for (int end = array.length; end > 0; end--) {
            boolean sorted =true ;
            for (int i = 1; i < end; i++) {
                if (array[i-1] > array[i]) {
                    Swap(array , i-1 , i); //交换数组两个元素，具体代码不再进行书写！
                    sorted = false;
                }
            }
            if (sorted == true) {
                break; //当没有进行交换的时候，说明已经排好序了！
            }
        }
    }

对于上述的代码，涉及到了嵌套的for循环，所以显得有点思维含量了！！

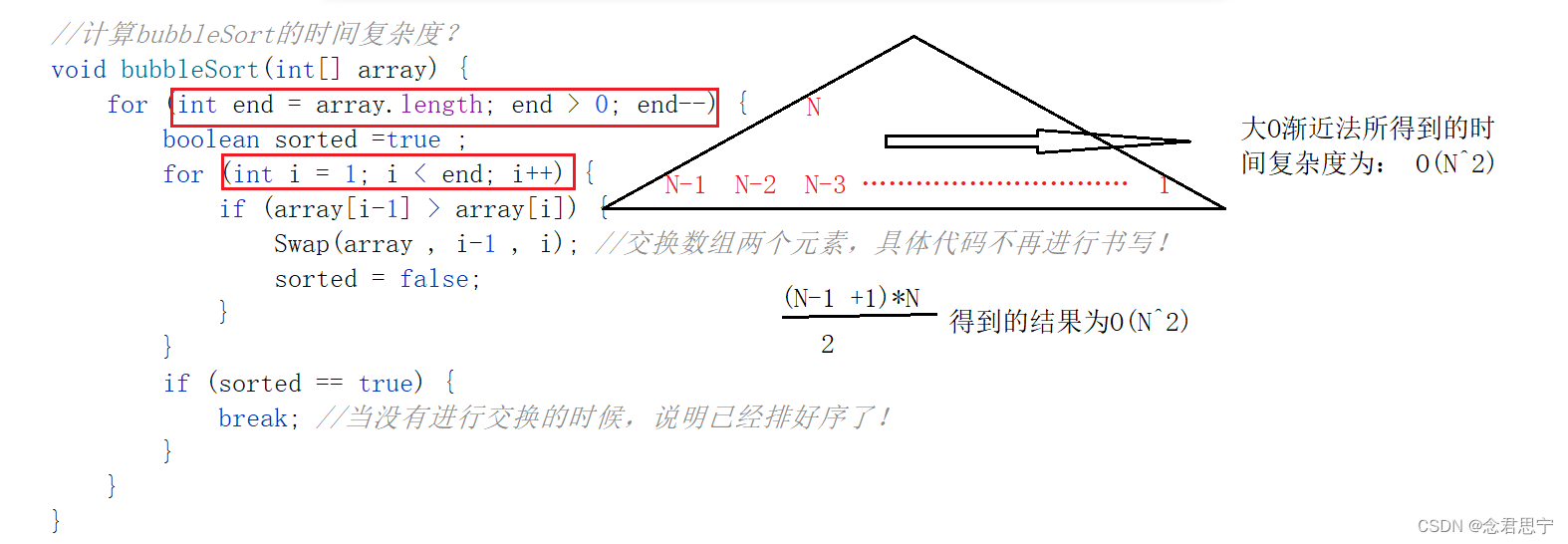
因此上述代码用大O渐进法来求时间复杂度为O(N^2)

计算下列代码的时间复杂度？

    //计算下列代码的时间复杂度？
    public static void bubbleSort(int[] array) {
        for (int i = 0; i < array.length; i++) {
            boolean flg = false;
            for (int j = 0; j < array.length-1-i; j++) {
                if (array[j] > array[j+1]) {
                    int tmp = array[j];
                    array[j] = array[j+1];
                    array[j+1] =tmp;
                }
            }
            if (flg == false) {
                return ;
            }
        }
    }

其实这个代码的时间复杂度的分析思路跟上面那个代码的分析思路是一样的，在此，笔者便不再做过多的讲解！！

计算binarySearch（二分查找）的时间复杂度??

    //计算binarySearch的时间复杂度??
    int binarySearch(int[] array ,int value) {
        int begin =0;
        int end =array.length-1;
        while (begin <= end) {
            int mid = begin + ((end-begin)/2);
            if (array[mid] < value) {
                begin = mid+1;
            }else if (array[mid]  > value) {
                end =mid-1;
            }else {
                return mid;
            }
            return -1;
        }
    }

上述代码是一个典型的二分查找的代码！！不信的读者可以自行测试！！在此笔者就不再进行过多的讲解如何进行书写的了！！

对于这个二分查找的代码，其实时间复杂度为：O(logN)在Java当中，习惯将以2为底的log去掉2！！

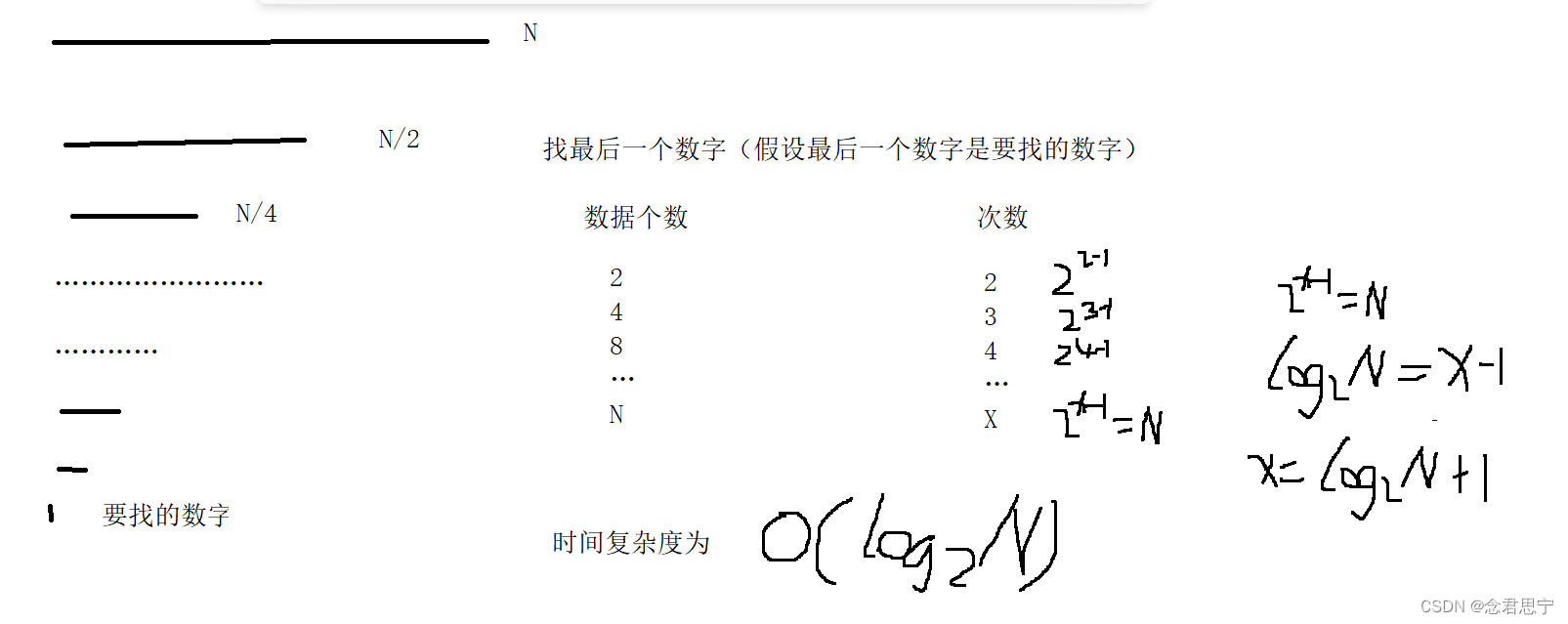
上述代码的简单解析便在上图！！其实，对于二分查找的时间复杂度不在于记住！！而在于学会了这个方法！！简单建议！学会方法！！在笔者学习的时候，很多老铁都是事后记住了 最后的结果，但是，对于推到的过程确实……忘了！！

难度上升一下：

计算阶乘递归factorial的时间复杂度？？

  //计算阶乘递归factorial的时间复杂度？？
    long factorial(int N) {
        return N < 2 ? N :factorial(N-1)*N;
    }

对于上述代码，这个是我们在学习递归思想的一个简单列题，不知道大家是否还能记得？？

对于递归的时间复杂度的计算方法跟上面的不太一样！！

递归的时间复杂度的计算方法为：

                                             递归的次数 * 每次递归后代码执行的次数！！

其实对于这个 公式，笔者到目前为止，运用还不是很清晰！！只能大概的讲述一下！！

在上述代码中，每次递归过来之后，代码都会执行一次三目运算符，则，每次递归后，代码的执行次数为1，但是，对于上述的代码，一共执行N次，所以，时间复杂度为：O(N)

计算斐波那契数递归的时间复杂度？？

  //计算斐波那契数递归的时间复杂度？？
    long fibonacci(int N) {
        return N < 2 ? N :fibonacci(N-1) + factorial(N-2);
    }

对于这个代码，显得有点儿难度上升了！！

在上述代码中，每次递归过来之后，代码都会执行一次三目运算符，则，每次递归后，代码的执行次数为1。

下面笔者画图来带领大家分析一下，简单的思路！！

上面便是时间复杂度的简单计算方法！！这些都是 笔者在学习的时候所接触过的列子！！

对于空间复杂度……在现实生活中，其实所要求的并不是很多，毕竟现在内存很大了！不再追求空间的效率了！但是，更多的时在于追求时间效率！！所以，笔者对于空间复杂度便不再做过多的讲解了！！若有其他的不同想法，请及时私聊笔者哟！！