leetcode原题链接：从前序与中序遍历序列构造二叉树

题目描述

       给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

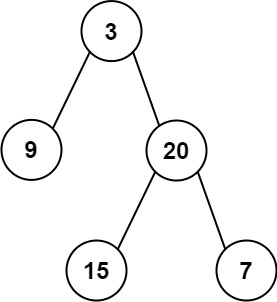
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

解题方法：

先序遍历的访问顺序： 根（左子树）(右子树）

中序遍历的访问树序：（左子树） 根 （右子树）

所以，根据先序遍历顺序，可以找到当前的root节点，根据中序遍历中root节点的位置，可以计算出左子树的个数和右子树的个数，这样就可以推算出先序遍历中左子树和右子树各自的起始位置。

注意，这里细节比较多，避免写错的方法就是计算出左右子树的节点的个数，然后根据节点个数的起始位置推算出左子树和右子树的范围。

C++代码

#include <iostream>
#include <vector>
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(std::vector<int>& preorder, std::vector<int>& inorder) {
        int n = preorder.size();
        int n1 = inorder.size();
        if (n != n1) {
            return nullptr;
        }
        return help(preorder, 0, n - 1, inorder, 0, n - 1);
    }

    TreeNode* help(std::vector<int>& preorder, int pre_left, int pre_right, 
                   std::vector<int>& inorder, int in_left, int in_right) {
        int n = preorder.size();
        int n1 = inorder.size();
        if (n != n1) {
            return nullptr;
        }
        if (pre_left == pre_right) {
            return new TreeNode(preorder[pre_left]);
        }
        int mid = -1;
        //找到根节点在中序遍历中的位置
        for (int index = in_left; index <= in_right; index++) {
            if (inorder[index] == preorder[pre_left]) {
                mid = index;
                break;
            }
        }
        if (mid == -1) {
            return nullptr;
        }
        int left_size = mid - 1  - in_left + 1; //计算左子树节点的个数
        int right_size = in_right - (mid + 1) + 1;//计算右子树节点的个数
        TreeNode* root = new TreeNode(inorder[mid]);
        if (root == nullptr) {
            return nullptr;
        }
        root->left = help(preorder, pre_left + 1, pre_left + left_size, 
                          inorder, in_left, mid - 1);//构造左子树
        root->right = help(preorder, pre_right - right_size + 1, pre_right, 
                          inorder, mid + 1, in_right);//构造右子树
        return root;
    }
};