贪心算法又称贪婪算法，是一种常见的算法思想。贪心算法的优点是效率高，实现较为简单，缺点是可能得不到最优解。

贪心算法的基本思想

贪心算法就是在求解问题时，总是做出当前看来最好的选择。也就是说贪心算法并不从整体最优上考虑问题，算法得到的是局部最优解。而局部最优解叠加在一起便构成了问题的整体最优解，或者近似最优解。

假设有3枚硬币，面值分别为1元、5角、1角。这3种硬币数量不限，现在要找给顾客2元7角。请问怎样才能使得找给顾客的硬币数量最少？

最直观的策略是尽量选择面值较大的硬币，在选取硬币时可以依照以下步骤：

找出不超过2元7角面值最大的硬币，也就是1元硬币。
此时还差1元7角，找出不超过1元7角的面值最大的硬币，也就是1元硬币。
此时还差7角，找出不超过7角的面值最大的硬币，也就是5角的硬币。
此时还差2角，找出一个不超过2角的面值最大的硬币，即1角硬币。
此时还差1角，找出一个不超过1角的面值最大的硬币，即1角硬币。
找钱过程结束。

上述找钱过程遵循了贪心算法的思想。在每次找钱的时候不关注整体最优，只关注当前还亏欠顾客的钱数子问题，并以此为基础选取不超过这个钱数的面值最大的硬币，即局部最优解。按照这个策略，最终找给顾客的硬币数量就是最少的。

贪心算法每一步只考虑局部最优解，所以在处理问题的时候可能得不到整体最优解。要使贪心算法得到最优解，问题应具备以下性质：

贪心选择性质

所求问题的整体最优解可以通过一系列局部最优解得到。例如在上面的找钱问题中，当前状态下最优的选择就是使找过硬币后还亏欠顾客的钱数最接近0，所以在每次找钱的时候都要选择面值尽可能大的硬币，这样硬币的总数才会更少。

最优子结构性质

当一个问题的最优解包含它的子问题的最优解时，则称该问题具有最有子结构性质。上述找钱问题就是典型的具有最优子结构性质的问题。
实际应用中的许多问题都可以使用贪心算法得到最优解，即使得不到最优解，也能得到最优解的近似解。所以在解决一般性问题时，我们可以大胆尝试使用贪心算法。
哈夫曼编码算法、图算法中的最小生成树Prim算法和Kruskal算法，以及计算图的单源最短路径的Dijkstra算法等都是基于贪心算法的思想设计的。

分薄饼问题

幼儿园的老师给小朋友们分薄饼。已知每个小朋友最多只能分到一块薄饼，对于每个小朋友i，都有一个需求值gi，即能让小朋友i满足需求的薄饼的最小尺寸。同时每块薄饼j都有一个尺寸sj，如果sj≥gi，就可以将薄饼j分给小朋友i。输出最多能满足几位小朋友。

这道题可以使用穷举法解决，去除不满足要求的组合，剩下的组合数量即为本题的答案。
我们只要遵循“用尽量小尺寸的薄饼满足不同小朋友的需求值”这一贪心策略，就可以得到本题的最优解。

#include<iostream>
#include<algorithm>

int getContentedChildren(int g[], int sizeofG, int s[], int sizeofS) {
	std::sort(g, g + sizeofG);
	std::sort(s, s + sizeofS);
	//g需求下标，s饼下标，count记录满足的数量
	int i = 0, j = 0, count = 0;
	while (i < sizeofG && j < sizeofS) {
		//g需求的尺寸小于等于s
		if (g[i] <= s[j]) {
			count++;
			i++;
			j++;
		}
		else {
			//g需求的尺寸大于s，则使用更大尺寸的s去匹配
			j++;
		}
	}
	return count;
}

int main() {
	int g[] = { 1,2 };
	int s[] = { 1,2,3 };
	std::cout << getContentedChildren(g, 2, s, 3);
}

C++标准算法库提供sort()排序方法，参数为STL始末迭代器或数组左右边界。
这个算法并不难理解，需要注意的是算法的开头部分，要对数组进行排序。

集合覆盖问题

有一个广播节目，要让全美50个州的听众都能收听到，为此，我们要决定在哪些广播台播出这个节目，在每个广播台播出都需要支付费用，所以要在尽可能少的广播台播出。现有广播台名单如下：

广播台名称	覆盖的州
KONE	ID、NV、UT
KTWO	WA、ID、MT
KTHREE	OR、NV、CA
KFOUR	NV、UT
KFIVE	CA、ZA

如果我们使用穷举法。假设全美有n个广播台可供选择，每种广播台都有“选择”和“不选择”两种状态，将这n个广播台中每个广播台的两种选择方式任意组合，共有 $2^n$ 种组合方式。现在我们要从这 $2^n$ 个集合中找出1个符合题意的集合。
这种方法简单直观，但非常耗时，时间复杂度达到了 $O(2^n)$ 。如果广播台数量不多，那么穷举法是可以的，可以在有限时间内找到问题的最优解。但是随着广播台的增多，消耗的时间将呈指数级增长，穷举法将不是可行的方案。

使用贪心算法进行解决。

我们通过一个简单的例子来理解贪心算法的精髓。假设现在只有9个州：ABCDEFGHI和5个广播台：12345。广播台对各州的覆盖情况如图所示：

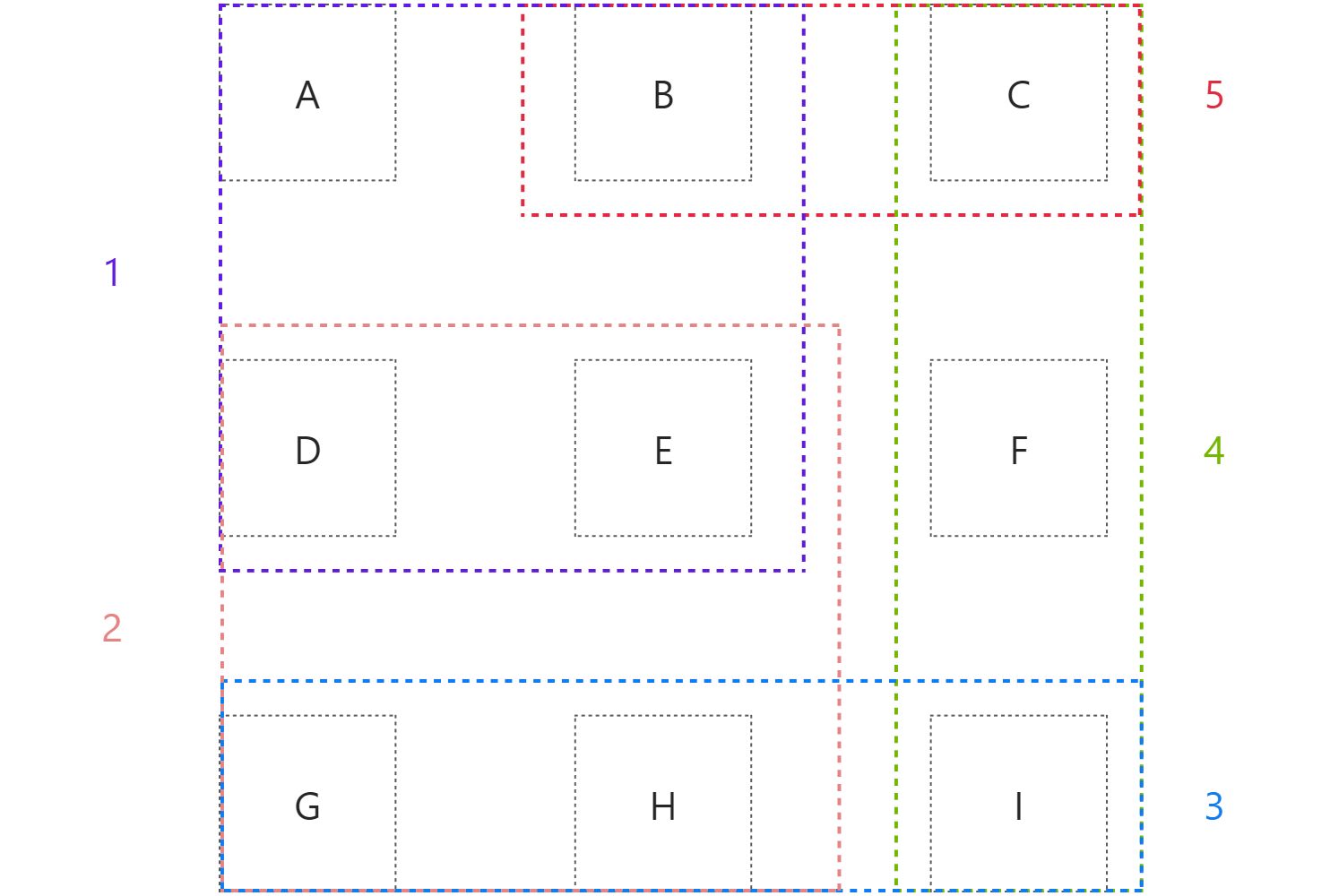
各个广播台覆盖情况如下：

广播台1覆盖的州为ABDE
广播台2覆盖的州为EDGH
广播台3覆盖的州为GHI
广播台4覆盖的州为CFI
广播台5覆盖的州为BC

现在，使用贪心算法来解决这个问题，步骤如下：

最初，未被覆盖的州为ABCDEFGHI。
选择可覆盖最多未覆盖州的广播台。广播台1、2均可覆盖4个州，这里选择广播台1。于是未覆盖的州变为CFGHI。
接下来选择能覆盖CFGHI中州最多的广播台，我们可选择计算交集的方法来找出这个广播台。广播台3和广播台4都可以覆盖3个未覆盖的州，这里选择广播台3。于是未覆盖的州变为CF。
接下来我们选择能覆盖CF中最多州的广播台。我们选择广播台4。

至此，9个州被广播台134覆盖：

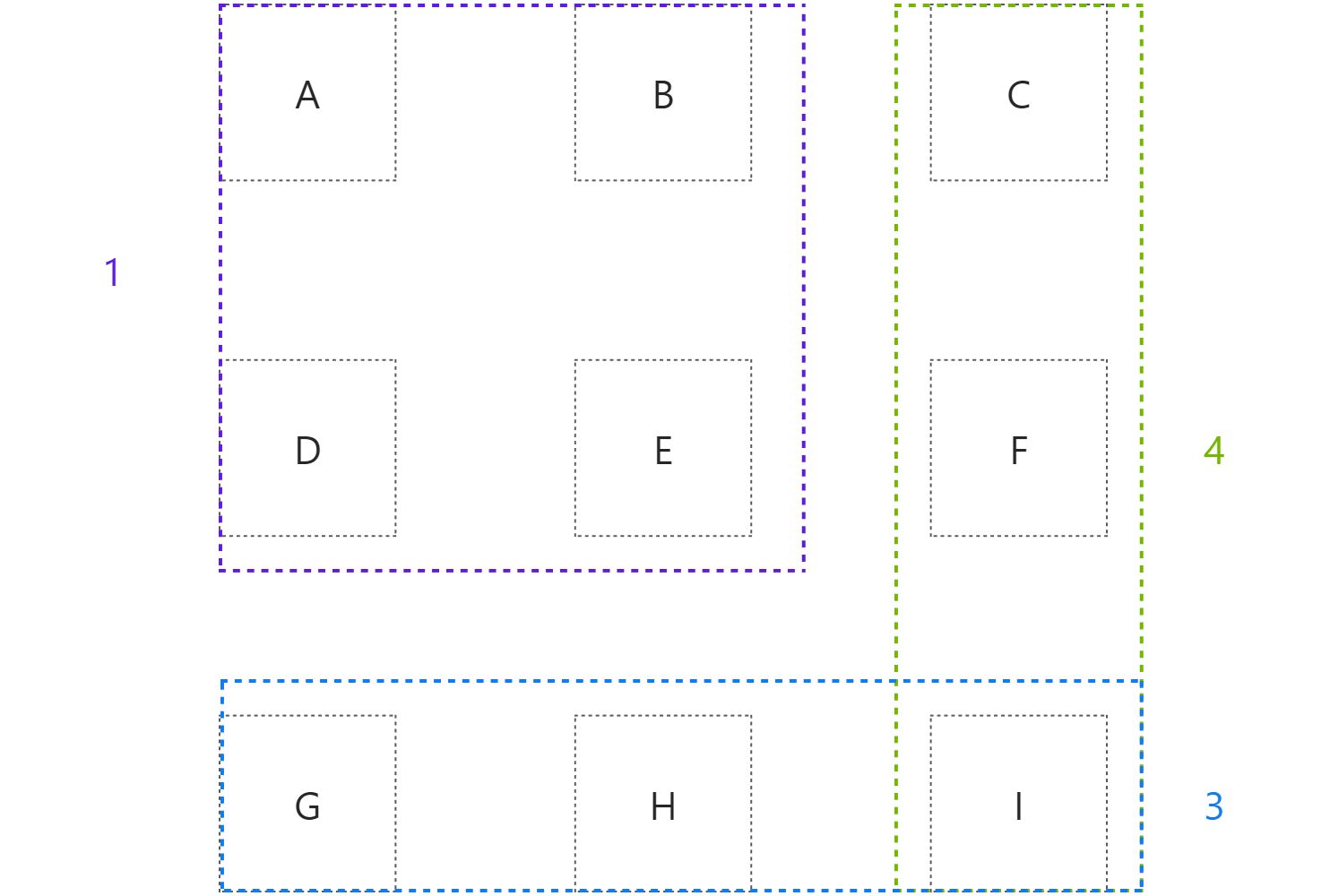
上述计算过程中，利用贪心策略逐步找出最优的广播台组合。使用贪心算法解决问题时并不从问题的整体最优解出发，而是“贪心“地着眼当下。贪心算法的时间复杂度为 $O(n^2)$ ，其中n为广播台的数量。
首先是函数的声明部分，我们要传入所有的州，所有的广播台以及每个广播台所能覆盖到的州。我们分别使用了HashSet和LinkedHashMap存储。返回值为所有最合适的广播台，我们使用HashSet存储。

//所有的州，所有的广播站以及对应的范围
public static HashSet<String> getBestBroadCasts(HashSet<String> allStatesSet, LinkedHashMap<String, HashSet<String>> broadCast) {
    HashSet<String> result = new HashSet<>();
    //待写
    return result;
}

接下来写中间部分，主要的函数体：

//外层循环控制覆盖所有周
while (allStatesSet.size() > 0) {
    HashSet<String> maxCovered = new HashSet<>();
    String tmpResult = "";
    //内层循环遍历每一个广播台，得到其覆盖的州
    for (Map.Entry<String, HashSet<String>> map : broadCast.entrySet()) {
        //得到该广播台可覆盖的州的集合
        HashSet<String> set = map.getValue();
        //计算该广播台可覆盖的州与未覆盖的州的交集
        HashSet<String> covered = new HashSet<>(set);
        covered.retainAll(allStatesSet);
        //maxCovered指向当前覆盖最广的广播台
        if (covered.size() > maxCovered.size()) {
            maxCovered = covered;
            tmpResult = map.getKey();
        }
    }
    result.add(tmpResult);
    allStatesSet.removeAll(maxCovered);
}

为了简化问题，我们使用了HashMap和HashSet结构存放数据。该容器类已经封装好了交、并、补操作。当我们需要去重时，可以直接调用。

import java.util.Arrays;
import java.util.HashSet;
import java.util.LinkedHashMap;

public class Main {
    public static void main(String[] args) {
        //初始化allStates，存放所有的州
        String allStates[] = {"mt", "wa", "or", "id", "nv", "ut", "ca", "az"};
        //将字符串数组转换为集合HashSet
        HashSet<String> allStatesSet = new HashSet<>(Arrays.asList(allStates));
        //创建一个Hash，存放广播台和每个广播台可覆盖的州
        LinkedHashMap<String, HashSet<String>> broadCasts = new LinkedHashMap<>();
        //初始化broadCasts
        broadCasts.put("kone", new HashSet<String>(Arrays.asList("id", "nv", "ut")));
        broadCasts.put("ktwo", new HashSet<String>(Arrays.asList("wa", "id", "mt")));
        broadCasts.put("kthree", new HashSet<String>(Arrays.asList("or", "nv", "ca")));
        broadCasts.put("kfour", new HashSet<String>(Arrays.asList("nv", "ut")));
        broadCasts.put("kfive", new HashSet<String>(Arrays.asList("ca", "az")));
        //验证结果
        System.out.println(Cast.getBestBroadCasts(allStatesSet, broadCasts));
    }
}