Day_61-62决策树(准备工作)

一. 算法的基本概念

1. 决策树的定义

2. 如何构建决策树？

2.1 熵

2.2 信息增益原则

2.3 计算步骤

二. 示例演示

1. 第一次节点决策分类：

2. 后续节点的决策分类

3. 决策分类的结束条件

三. 代码实现

1. 主函数

2. 两个构造函数

3. 打标签函数getMajorityClass和判定纯度函数pureJudge

4. 核心代码建立决策树

4.1 判定是否结束子树构造

4.2 根据信息增益原则寻找最优属性

4.3 根据最优属性进行分类

4.4 构造孩子节点和更新节点信息

5. 输出函数

6. 准确性检验

四. 运行结果

Day_61-62决策树(准备工作)

一. 算法的基本概念

1. 决策树的定义

决策树是一种机器学习的方法（参考这篇文章），决策树的生成算法有ID3, C4.5和C5.0等（这篇文章只讨论ID3）。决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

举一个简单的例子：

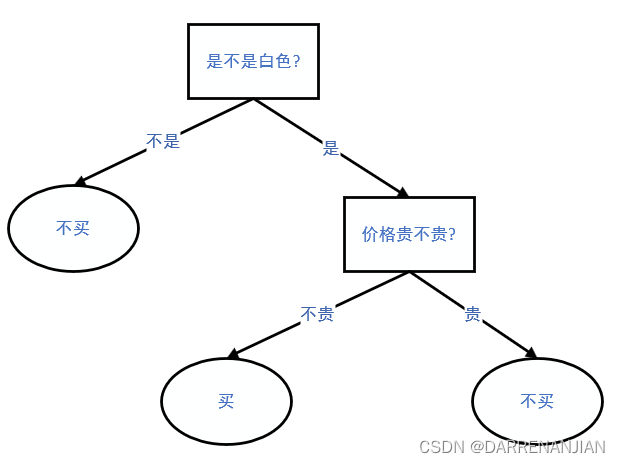
假设我要买一部手机，只考虑手机的两个方面:颜色和价格。我的心路历程是这样的：首先要看颜色，不是白色的我不喜欢，不买；然后看价格，本人价格敏感，太贵的不买。这个解决方案可以用一个流程图来描述，如图1所示。具体来说，这是一个树。方形就是我要判断的一个指标；有向边就是一个指标的取值；沿着有向边走到树的末端，就到了叶子节点——叶子节点就是我最终的决定。来一个手机，我按这个树描述的规则，进行判断，就可以知道我能不能买。

2. 如何构建决策树？

上面我们知道了上面是决策树，回顾一下目标，我们的目标是根据数据输出它的标签对不对？所以这里问题的关键是我们如何构建一个决策树。这里我们就开始介绍算法的基本概念

2.1 熵

学过信息论的读者应该都知道熵的概念（熵在其他的领域计算公式略有差异，这里以信息领域为准），1948年，香农将统计物理中熵的概念，引申到信道通信的过程中，香农定义的“熵”又被称为“香农熵”或“信息熵”。对于属性 $P_{1}$ 的熵即：

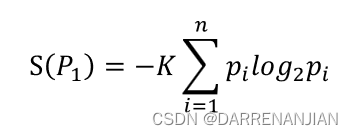
其中 $i$ 标记概率空间中所有可能的样本，表示 $p_{i}$ 该样本的出现几率， $K$ 是和单位选取相关的任意常数（这里我取 $K$ 为1）， $S$ 表示这个属性的最终熵值。这个概念是用于衡量信息的混乱程度的量，熵的值越高，表示数据集的混乱程度越高（纯度越低）；熵的值越低，表示数据集的混轮程度越高（纯度越低）。

条件熵表示在属性 $P_{i}$ 条件下判定结果的熵值，对于属性 $P_{1}$ 条件下判定结果的熵值

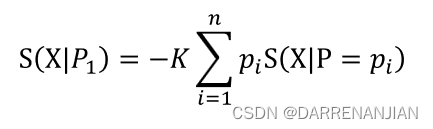
2.2 信息增益原则

对于某一个数据集，它可能有诸多属性，对于每一个属性，是否以它分类呢？这里引入信息增益的概念。对于某一个数据集 $D$ ，它的某一个属性为 $P_{i}$ ，那么在 $P_{i}$ 条件下的信息增益为 $g(D,P_{i})$ ，定义 $g(D,P_{i})$ 的计算公式如下所示，

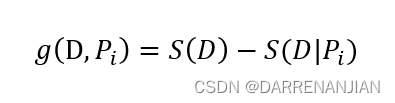
除此之外，对于每一个属性由于 $S(D)$ 都相等，之前是计算 $max\ g(D,P_{i})$ ，现在

$max(g(D,P_{i}))=max(S(D)-S(D|P_{i})) =max(-S(D|P_{i}))=min(S(D|P_{i}))$

2.3 计算步骤

①从根节点开始，计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的划分特征；

②由该特征的不同取值建立子节点；

③再对子节点递归1-2步，构建决策树；

④直到没有特征可以选择或类别完全相同为止，得到最终的决策树。

二. 示例演示

对于数据weather

@relation weather
@attribute Outlook {Sunny, Overcast, Rain}
@attribute Temperature {Hot, Mild, Cool}
@attribute Humidity {High, Normal, Low}
@attribute Windy {FALSE, TRUE}
@attribute Play {N, P}
@data
Sunny,Hot,High,FALSE,N
Sunny,Hot,High,TRUE,N
Overcast,Hot,High,FALSE,P
Rain,Mild,High,FALSE,P
Rain,Cool,Normal,FALSE,P
Rain,Cool,Normal,TRUE,N
Overcast,Cool,Normal,TRUE,P
Sunny,Mild,High,FALSE,N
Sunny,Cool,Normal,FALSE,P
Rain,Mild,Normal,FALSE,P
Sunny,Mild,Normal,TRUE,P
Overcast,Mild,High,TRUE,P
Overcast,Hot,Normal,FALSE,P
Rain,Mild,High,TRUE,N

1. 第一次节点决策分类：

计算属性Outlook下的信息增益：

$S(play|Sunny)=-3/5\cdot log(3/5)-2/5\cdot log(2/5)=0.673$

$S(play|Overcast)=0-1\cdot log1=0$

$S(play|Rain)=-2/5\cdot log(2/5)-3/5\cdot log(3/5)=0.673$

故最终的条件熵为:

$S(play|Outlok)=-5/14\cdot 0.673-0-5/14\cdot 0.673=0.4807$

同理计算另外三个属性的条件熵：

$S(play|Temperature)=0.6315$

$S(play|Humidity)=0.6315$

$S(play|Windy)=0.6183$

由上述的公式可知，根据最大化信息增益准则，用Outlook属性作为第一个节点的分类标准最为合适。

2. 后续节点的决策分类

同样的道理，上述过程完成了对于第一个节点的决策分类，对于第二个节点也需要进行上述的决策分类，需要注意的是，这里的条件熵已经改变了部分数据集，需要重新判定，例如对于sunny下述数据，hot有2个，mild有2个，cool有1个，现在的条件熵为

$S(play|Hot)=-1\cdot log(1)-0\cdot log(0)=0$

$S(play|Mild)=-1/2\cdot log(1/2)-1/2\cdot log(1/2)=0.6931$

$S(play|Cool)=-0\cdot log(0)-1\cdot log(1)=0$

对应的条件熵

$S(play|Temperature)=-2/5\cdot 0-2/5\cdot 0.6931-1/5\cdot 0=0.2722$

对应另外的属性同理,也就是说，没当经过一个节点的分类之后，所选取的空间发生改变，对应的概率和熵值也会发生改变。

3. 决策分类的结束条件

当什么时候决策分类结束呢?当这个节点的所有结果都是一致的时候，结束决策分类(结果作为叶子节点)，对应上式的信息增益为1（因为S（D）=1，S(D|P)=0）结束分类。

最终构造完成的决策树

三. 代码实现

1. 主函数

这一段代码主要是看第二段，传入所有数据构成一个节点tempID3，设置临界阈值为3（表示当数据个数＜3之后结束判定分类）；根据这个节点tempID3建树；输出建树的结果；检验测试（由训练数据作为测试数据，考察准确度）。

这里最重要的是理解理解建树的递归思想（我们是根据这个tempID3节点建树，若条件满足则继续向下建树，不满足则退出）；其次检验函数也需要用到递归思想，为方便理解我待会会在后面叙述。

    /**
     *************************
     * Test this class.
     *
     * @param args
     *            Not used now.
     *************************
     */
    public static void main(String[] args) {

        id3Test();
    }// Of main

    /**
     *************************
     * Test this class.
     *
     * @param args
     *            Not used now.
     *************************
     */
    public static void id3Test() {
        ID3 tempID3 = new ID3("D:/data/weather.arff");
        // ID3 tempID3 = new ID3("D:/data/mushroom.arff");
        ID3.smallBlockThreshold = 3;
        tempID3.buildTree();

        System.out.println("The tree is: \r\n" + tempID3);

        double tempAccuracy = tempID3.selfTest();
        System.out.println("The accuracy is: " + tempAccuracy);
    }// Of id3Test

2. 两个构造函数

第一个构造函数主要是在程序开始的时候传入数据，

①输入路径，根据路径找到数据data，再根据data创建instance类的dataset对象，创建失败则抛出异常。

②setClassIndex函数设置标签对应的是哪一个属性（4），numClasses记录标签种类的个数（以天气数据为例，只有去玩和不去玩两种，故numClasses=2）

③availableInstances是这个节点的所有数据，可以理解为要分类的数据索引；availableAttributes是除去标签的属性数组（availableAttributes数组的每一个空记录是第几个属性（也表示这个节点还可能对哪几个属性判定分类））

④初始化孩子为null（因为还没有判断）；getMajorityClass根据此时的数据情况得到这个节点的标签（这一点其实没什么用，除了在叶子节点对标签的判断外，在非叶子节点判断无用，不过因为是同一个对象，可能也就判断了）；pureJudge函数判定是否数据“纯”，即这个节点的数据的标签是否都是一类。

    /**
     ********************
     * The constructor.
     *
     * @param paraFilename
     *            The given file.
     ********************
     */
    public ID3(String paraFilename) {
        dataset = null;
        try {
            FileReader fileReader = new FileReader(paraFilename);
            dataset = new Instances(fileReader);
            fileReader.close();
        } catch (Exception ee) {
            System.out.println("Cannot read the file: " + paraFilename + "\r\n" + ee);
            System.exit(0);
        } // Of try

        dataset.setClassIndex(dataset.numAttributes() - 1);
        numClasses = dataset.classAttribute().numValues();

        availableInstances = new int[dataset.numInstances()];
        for (int i = 0; i < availableInstances.length; i++) {
            availableInstances[i] = i;
        } // Of for i
        availableAttributes = new int[dataset.numAttributes() - 1];
        for (int i = 0; i < availableAttributes.length; i++) {
            availableAttributes[i] = i;
        } // Of for i

        // Initialize.
        children = null;
        // Determine the label by simple voting.
        label = getMajorityClass(availableInstances);
        // Determine whether or not it is pure.
        pure = pureJudge(availableInstances);
    }// Of the first constructor

第二个构造函数待会运行到的时候再说明。

3. 打标签函数getMajorityClass和判定纯度函数pureJudge

首先是getMajorityClass函数，这个时候只有一个节点可能理解比较简单，但是对于后面将孩子分类之后打标签就可能理解不了。其实本质上都是一样的，现在的所有数据都集中在如下的节点。

我们根据这个节点的所有标签个数（去玩还是不去玩），谁多就打上谁的标签（对于这个节点，不去玩的个数少于去玩的个数，所以标签是不去玩）

这个函数的作用就是我们学习得到的判定结果，待会需要和原本已知的数据作比较得到准确度。

    /**
     **********************************
     * Compute the majority class of the given block for voting.
     *
     * @param paraBlock
     *            The block.
     * @return The majority class.
     **********************************
     */
    public int getMajorityClass(int[] paraBlock) {
        int[] tempClassCounts = new int[dataset.numClasses()];
        for (int i = 0; i < paraBlock.length; i++) {
            tempClassCounts[(int) dataset.instance(paraBlock[i]).classValue()]++;
        } // Of for i

        int resultMajorityClass = -1;
        int tempMaxCount = -1;
        for (int i = 0; i < tempClassCounts.length; i++) {
            if (tempMaxCount < tempClassCounts[i]) {
                resultMajorityClass = i;
                tempMaxCount = tempClassCounts[i];
            } // Of if
        } // Of for i

        return resultMajorityClass;
    }// Of getMajorityClass

接着是“纯度函数”pureJudge，还是根据这个节点的所有数据判断纯度，若所有的标签都一致，则输出为true；否则则输出false。这个函数的主要作用是判断是否结束某一个子树向下的延伸，即我还需不需要再加孩子扩充决策树。

    /**
     **********************************
     * Is the given block pure?
     *
     * @param paraBlock
     *            The block.
     * @return True if pure.
     **********************************
     */
    public boolean pureJudge(int[] paraBlock) {
        pure = true;

        for (int i = 1; i < paraBlock.length; i++) {
            if (dataset.instance(paraBlock[i]).classValue() != dataset.instance(paraBlock[0])
                    .classValue()) {
                pure = false;
                break;
            } // Of if
        } // Of for i

        return pure;
    }// Of pureJudge

4. 核心代码建立决策树

这部分代码是核心，主要理解三个点：①怎么样用递归建立决策树②怎么样对数据进行划分③怎么样对已使用和未使用的属性进行判别。

    /**
     **********************************
     * Build the tree recursively.
     **********************************
     */
    public void buildTree() {
        if (pureJudge(availableInstances)) {
            return;
        } // Of if
        if (availableInstances.length <= smallBlockThreshold) {
            return;
        } // Of if

        selectBestAttribute();
        int[][] tempSubBlocks = splitData(splitAttribute);
        children = new ID3[tempSubBlocks.length];

        // Construct the remaining attribute set.
        int[] tempRemainingAttributes = new int[availableAttributes.length - 1];
        for (int i = 0; i < availableAttributes.length; i++) {
            if (availableAttributes[i] < splitAttribute) {
                tempRemainingAttributes[i] = availableAttributes[i];
            } else if (availableAttributes[i] > splitAttribute) {
                tempRemainingAttributes[i - 1] = availableAttributes[i];
            } // Of if
        } // Of for i

        // Construct children.
        for (int i = 0; i < children.length; i++) {
            if ((tempSubBlocks[i] == null) || (tempSubBlocks[i].length == 0)) {
                children[i] = null;
                continue;
            } else {
                // System.out.println("Building children #" + i + " with
                // instances " + Arrays.toString(tempSubBlocks[i]));
                children[i] = new ID3(dataset, tempSubBlocks[i], tempRemainingAttributes);

                // Important code: do this recursively
                children[i].buildTree();
            } // Of if
        } // Of for i
    }// Of buildTree

4.1 判定是否结束子树构造

回到我们之前的过程，我们现在已经建立了一个节点——原数据集，现在对这个节点进行判断，若它已经是“纯”数据了（标签一致）直接结束；若它的数据个数≤smallBlockThreshold直接结束。显然两个条件都没有满足。

4.2 根据信息增益原则寻找最优属性

现在我们就需要对这部分数据进行分类selectBestAttribute函数的作用是选出最佳的分类属性：根据现在的属性个数（0,1,2,3）做循环，计算每一个的条件熵（上面的公式推导过，因为S（D）都是一致的，所有我们只需要计算条件熵）。到条件熵函数conditionalEntropy：传入一个属性paraAttribute，构造数组用于记录paraAttribute属性下的每个具体属性的个数，构造tempCountMatrix用于记录每个具体属性下标签的个数。

接着开始计算条件熵，第一重循环对某一个属性的具体属性个数循环i，第二重循环对标签的个数循环j，现在的概率pi=tempCountMatrix[i][j]/ tempValueCounts[i]，对于某一个具体属性的条件熵tempEntropy-=p1*logp1-p2*logp2（这里2是标签的个数），最后计算某一个属性的条件熵resultEntropy=resultEntropy+tempValueCounts[i]（某个具体属性的所有个数）/数据总数tempNumInstances*tempEntropy某个属性的条件熵。

最后记录下最小的条件熵，输出它的类别，即完成了selectBestAttribute（）的作用。

    /**
     **********************************
     * Select the best attribute.
     *
     * @return The best attribute index.
     **********************************
     */
    public int selectBestAttribute() {
        splitAttribute = -1;
        double tempMinimalEntropy = 10000;
        double tempEntropy;
        for (int i = 0; i < availableAttributes.length; i++) {
            tempEntropy = conditionalEntropy(availableAttributes[i]);
            if (tempMinimalEntropy > tempEntropy) {
                tempMinimalEntropy = tempEntropy;
                splitAttribute = availableAttributes[i];
            } // Of if
        } // Of for i
        return splitAttribute;
    }// Of selectBestAttribute

    /**
     **********************************
     * Compute the conditional entropy of an attribute.
     *
     * @param paraAttribute
     *            The given attribute.
     *
     * @return The entropy.
     **********************************
     */
    public double conditionalEntropy(int paraAttribute) {
        // Step 1. Statistics.
        int tempNumClasses = dataset.numClasses();
        int tempNumValues = dataset.attribute(paraAttribute).numValues();
        int tempNumInstances = availableInstances.length;
        double[] tempValueCounts = new double[tempNumValues];
        double[][] tempCountMatrix = new double[tempNumValues][tempNumClasses];

        int tempClass, tempValue;
        for (int i = 0; i < tempNumInstances; i++) {
            tempClass = (int) dataset.instance(availableInstances[i]).classValue();
            tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
            tempValueCounts[tempValue]++;
            tempCountMatrix[tempValue][tempClass]++;
        } // Of for i

        // Step 2.
        double resultEntropy = 0;
        double tempEntropy, tempFraction;
        for (int i = 0; i < tempNumValues; i++) {
            if (tempValueCounts[i] == 0) {
                continue;
            } // Of if
            tempEntropy = 0;
            for (int j = 0; j < tempNumClasses; j++) {
                tempFraction = tempCountMatrix[i][j] / tempValueCounts[i];
                if (tempFraction == 0) {
                    continue;
                } // Of if
                tempEntropy += -tempFraction * Math.log(tempFraction);
            } // Of for j
            resultEntropy += tempValueCounts[i] / tempNumInstances * tempEntropy;
        } // Of for i

        return resultEntropy;
    }// Of conditionalEntropy

4.3 根据最优属性进行分类

上面我们已经找出了最优的属性splitAttribute，splitData是将现在的节点数据按最优属性划分出来，返回根据最优属性splitAttribute构建的二维数组，行表示每一个具体的属性，列表示对应的数据索引。

    /**
     **********************************
     * Split the data according to the given attribute.
     *
     * @return The blocks.
     **********************************
     */
    public int[][] splitData(int paraAttribute) {
        int tempNumValues = dataset.attribute(paraAttribute).numValues();
        // System.out.println("Dataset " + dataset + "\r\n");
        // System.out.println("Attribute " + paraAttribute + " has " +
        // tempNumValues + " values.\r\n");
        int[][] resultBlocks = new int[tempNumValues][];
        int[] tempSizes = new int[tempNumValues];

        // First scan to count the size of each block.
        int tempValue;
        for (int i = 0; i < availableInstances.length; i++) {
            tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
            tempSizes[tempValue]++;
        } // Of for i

        // Allocate space.
        for (int i = 0; i < tempNumValues; i++) {
            resultBlocks[i] = new int[tempSizes[i]];
        } // Of for i

        // Second scan to fill.
        Arrays.fill(tempSizes, 0);
        for (int i = 0; i < availableInstances.length; i++) {
            tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
            // Copy data.
            resultBlocks[tempValue][tempSizes[tempValue]] = availableInstances[i];
            tempSizes[tempValue]++;
        } // Of for i

        return resultBlocks;
    }// Of splitData

4.4 构造孩子节点和更新节点信息

首先更新其余属性的值，由于我们已经选出了最优属性，现在需要将这个属性从之前的属性组availableAttributes剥离开来。接着构造孩子节点：由于splitData函数返回的是分好类的二维数组，我们根据这个二维数组构建孩子节点，每个孩子节点的数据是数组tempSubBlocks的一行。接着递归操作，建树。

5. 输出函数

    /**
     *******************
     * Overrides the method claimed in Object.
     *
     * @return The tree structure.
     *******************
     */
    public String toString() {
        String resultString = "";
        String tempAttributeName = dataset.attribute(splitAttribute).name();
        if (children == null) {
            resultString += "class = " + label;
        } else {
            for (int i = 0; i < children.length; i++) {
                if (children[i] == null) {
                    resultString += tempAttributeName + " = "
                            + dataset.attribute(splitAttribute).value(i) + ":" + "class = " + label
                            + "\r\n";
                } else {
                    resultString += tempAttributeName + " = "
                            + dataset.attribute(splitAttribute).value(i) + ":" + children[i]
                            + "\r\n";
                } // Of if
            } // Of for i
        } // Of if

        return resultString;
    }// Of toString

6. 准确性检验

主要是理解test函数和classify函数

对于test函数，做leave-out-leave测试，若检测classify(paraDataset.instance(i))每一个实例值和原数据不相对应的话，correct自加1。

对于classify函数：若此时孩子节点为null（表示该节点为叶子节点）输出标签；若不然tempChild指向决策树的子节点，若tempChild为null（表示没有以这个属性分类的节点）输出标签。最后递归paraInstance。

    /**
     **********************************
     * Classify an instance.
     *
     * @param paraInstance
     *            The given instance.
     * @return The prediction.
     **********************************
     */
    public int classify(Instance paraInstance) {
        if (children == null) {
            return label;
        } // Of if

        ID3 tempChild = children[(int) paraInstance.value(splitAttribute)];
        if (tempChild == null) {
            return label;
        } // Of if

        return tempChild.classify(paraInstance);
    }// Of classify

    /**
     **********************************
     * Test on a testing set.
     *
     * @param paraDataset
     *            The given testing data.
     * @return The accuracy.
     **********************************
     */
    public double test(Instances paraDataset) {
        double tempCorrect = 0;
        for (int i = 0; i < paraDataset.numInstances(); i++) {
            if (classify(paraDataset.instance(i)) == (int) paraDataset.instance(i).classValue()) {
                tempCorrect++;
            } // Of i
        } // Of for i

        return tempCorrect / paraDataset.numInstances();
    }// Of test

    /**
     **********************************
     * Test on the training set.
     *
     * @return The accuracy.
     **********************************
     */
    public double selfTest() {
        return test(dataset);
    }// Of selfTest