💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，方便大家进行学习！亲民！！！
📝目前更新：🌟🌟🌟电力系统相关知识，期刊论文，算法，机器学习和人工智能学习。
🚀支持：🎁🎁🎁如果觉得博主的文章还不错或者您用得到的话，可以关注一下博主，如果三连收藏支持就更好啦！这就是给予我最大的支持！

​

📋📋📋本文目录如下：⛳️⛳️⛳️

​

目录

1 概述

2 数学模型 

3 结果

4 Matlab代码实现

---

1 概述

中国的高电压技术在全世界都是领先地位，很值得我们自豪！

高压直流输电（HVDC）是一种成熟的技术，可以远距离输电，也可以在不同步的网络之间实现互联互通。最常见的高压直流配置（即点对点）包括两个通过架空电力线或海底电缆连接的换流站，如图1a所示。然而，未来的电力系统将需要网状直流网络用于SuperGrids [1]和海上风电场[2]等应用。这种类型的直流电网，即多终端高压直流输电系统（MT-HVDC），由于高功率力换向半导体器件和直流断路器的发展而可行[3]。

最近的研究表明，密集网状多终端高压直流输电网在效率和安全性方面具有优势[4]。但是，这些类型的网格比传统的点对点线更难控制。它们需要终端和优化算法之间的可靠通信，以找到最佳工作点。

此外，高度网格化的MT-HVDC系统要求DC/DC站互连具有不同标称电压或不同配置（例如单极，双极，同极）的HVDC系统。DC/DC站可以控制特定HVDC线路上的有功功率（见图1b），并在直流故障等干扰期间协助MT-HVDC。

电力系统运行的传统方法，如最佳潮流（OPF），必须适应这种新环境。就像其对应的AC [5]一样，多终端高压直流输电系统的最佳功率流是一个非线性和非凸的问题。这在理论和实践上都是一个挑战。如果将DC/DC转换器包含在模型中，则复杂程度会增加，因为它们涉及额外的控制变量以及与功率损耗相关的非线性方程。

本文提出了多端高压直流输电系统最优潮流的非线性模型。所提出的方法仅考虑电网的直流侧，并包括带有DC / DC转换器的分支。优化模型中还考虑了线路损耗和DC/DC转换器。为了获得实时操作的唯一解，提出一种半定限近似方法。该方法在CIGRE B4直流电网测试系统的简化版本上进行评估。结果表明，与GAMS求解的非线性模型相比，所提出的近似是高效和准确的。

2 数学模型 

部分代码：

%% 特征值逼近
[V,D] = eig(X);
lm = diag(D);
vm = V(:,NumN);
vm*vm'*lm(NumN);
disp('---------------- 功率损耗 ----------------');
trace(G*X)
disp('---------------- 电压 --------------------');
Vap = sqrt(lm(NumN))*vm;
disp(Vap);
disp('---------------- 线路潮流-------------');
kk = 0;
for k = 1:NumL
    kk = kk +1;
    fprintf('%i%s%i%s%f\n',MT.Lines(k,1),' -> ',MT.Lines(k,2),' : ',F(kk));
    kk = kk +1;
    fprintf('%i%s%i%s%f\n',MT.Lines(k,2),' -> ',MT.Lines(k,1),' : ',F(kk));
end
disp('---------------- DC/DC 变换器 -----------');
Qp

%% 特征值逼近
[V,D] = eig(X);
lm = diag(D);
vm = V(:,NumN);
vm*vm'*lm(NumN);
disp('---------------- 功率损耗 ----------------');
trace(G*X)
disp('---------------- 电压 --------------------');
Vap = sqrt(lm(NumN))*vm;
disp(Vap);
disp('---------------- 线路潮流-------------');
kk = 0;
for k = 1:NumL
    kk = kk +1;
    fprintf('%i%s%i%s%f\n',MT.Lines(k,1),' -> ',MT.Lines(k,2),' : ',F(kk));
    kk = kk +1;
    fprintf('%i%s%i%s%f\n',MT.Lines(k,2),' -> ',MT.Lines(k,1),' : ',F(kk));
end
disp('---------------- DC/DC 变换器 -----------');
Qp
 

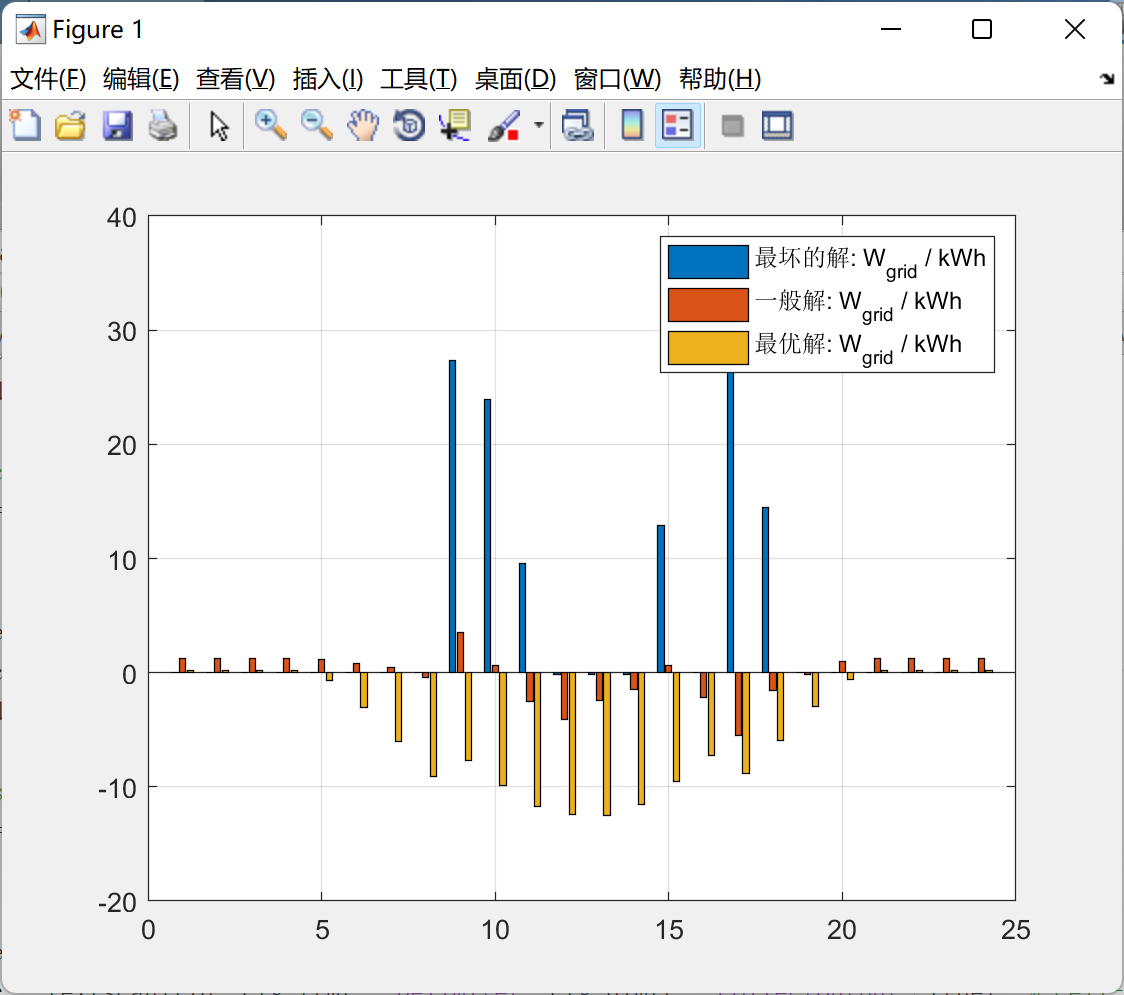
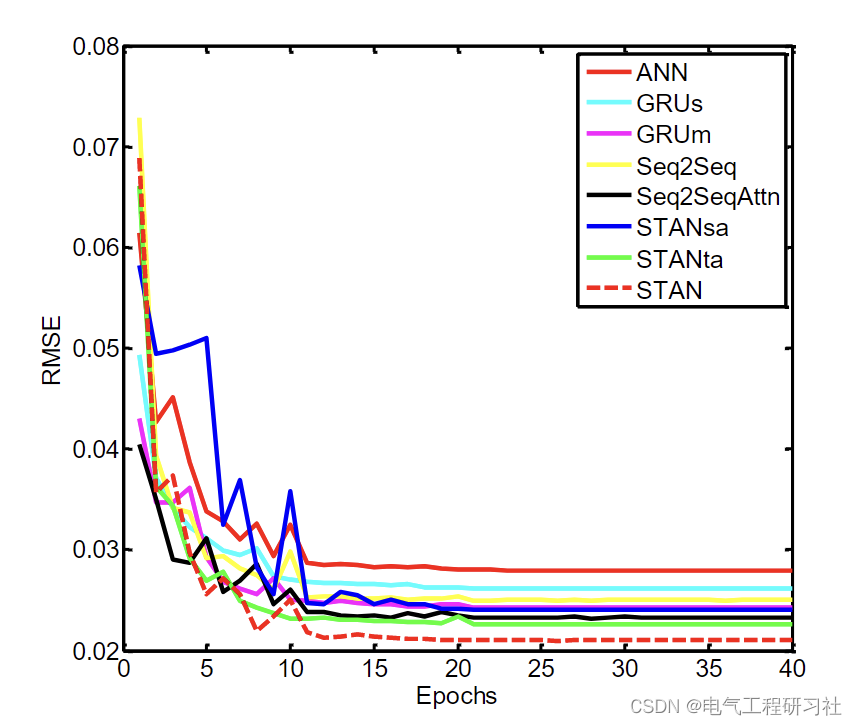
3 结果

4 Matlab代码实现

博客主页：电气辅导帮