一、概念
1、树的概念

树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树,是因为它看起来像是一棵倒挂的树,也就是说它的根在上,而叶子在下。
如果一个数的结点n为0,那么这个树叫做空树。反之,如果结点n>0,那么这个树是非空树T。
结点:树中的一个独立单元,如6、1、20、43等都是结点
结点的度:结点拥有的字数的个数或者分支的个数。例如6有3棵子树,那么结点6的度就是3。
树的度:树中各结点的度的最大值
叶子结点:又叫做终端结点。指度为0的结点,例如图中的5,23,29,8,32,10,0都是叶子结点。
非终端结点:又叫做分支结点。指度不为0的结点。
孩子:结点子树的根。如 6结点的孩子为1,20,43。
双亲:与孩子的定义对应。如 1,20,43结点的双亲为6。
兄弟:同一个双亲的孩子之间互为兄弟。如 1,20,43互为兄弟。
祖先:从根到该结点所经分支上的所有结点。
子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。
层次:结点的层次从根开始定义起,根为第一层,根的孩子为第二层。
堂兄弟:双亲在同一层的结点互为堂兄弟。
树的深度:树中结点的最大层次称为树的深度或高度。
有序树和无序树:如果将树中的结点的各子树看成从左到右是有次序的(即不能互换),则称该树为无序树。在有序树中最左边的子树的根称为第一个孩子,最右边的称为最后一个孩子。
森林:是m(m>0)棵互不相交的树的集合。
2、二叉树
二叉树(Binary Tree)是n(n>=0)个节点所构成的集合,每个节点最多有两棵子树,子树又有左右之分,分为左子树和右子树。
二叉树共有5种形态:
- 空二叉树
- 只有一个根结点的二叉树
- 只有左子树的二叉树
- 只有右子树的二叉树
- 既有左子树又有右子树的二叉树
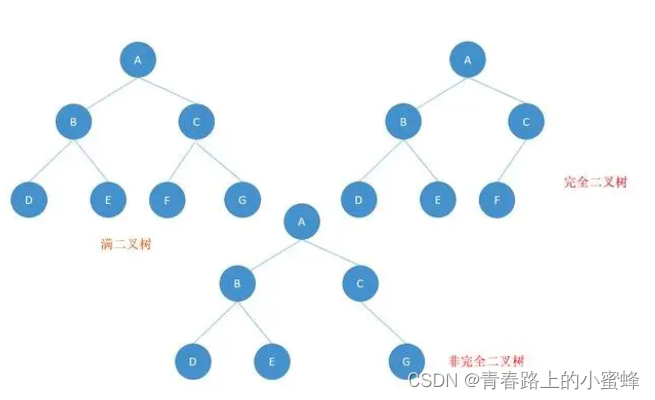
(1)满二叉树
如果一棵二叉树所有的分支节点都存在左子树和右子树,并且所有的叶子节点都在同一层上,这样的二叉树称为满二叉树
满二叉树具有如下特点:
叶子只能出现在最下一层
非叶子节点的度一定是2
同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
(2)完全二叉树
若二叉树的高度为h,除第h层外,其他(1~h-1层)的结点数都达到了最大个数,第h层有叶子节点,并且叶子节点都是从左到右依次排布,这就是完全二叉树。
完全二叉树的特点:
- 叶子节点只能出现在最下两层
- 最下层叶子节点在左侧并且连续
- 同样结点数的二叉树,完全二叉树的深度最小
注意:满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。
二叉树的存储结构有两种方式:顺序存储和链式存储
(3)二叉搜索树(二叉排序树)
- 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值
- 若它的右子树不为空,则右子树上所有结点的值都大于根结点的值。
- 它的左右子树也分别是二叉搜索树
注意:二叉搜索树的中序遍历的结果是有序的。
(4)平衡二叉树(又成AVL树)
用于解决二叉排序树高度不确定的情况,如果二叉排序树的高度相差太大,就会让二叉排序树的时间复杂度升级为O(n),为了避免这一情况,就出现了平衡二叉树,使树的高度尽可能的小,其本质还是一棵二叉搜索树。
平衡二叉树的性质:
- 左子树和右子树的高度之差的绝对值小于等于1
- 左子树和右子树也是平衡二叉树
(5)红黑树
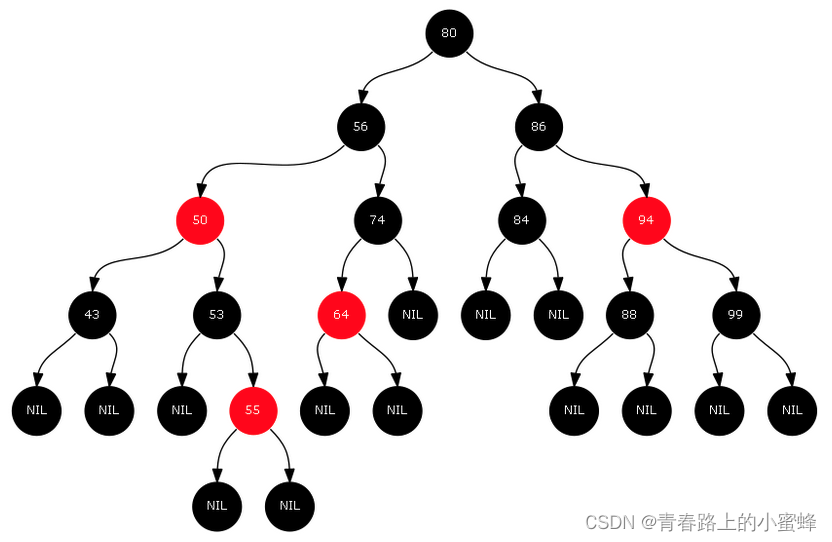
红黑树的特性:
- 每个节点要么是红色,要么是黑色
- 根结点为黑色
- 每个叶子节点(NIL)均为黑色【注:这里的叶子节点指的是空(NIL或者NULL)的叶子节点】
- 如果一个节点是红色,那么它的子节点必定是黑色
- 从一个节点到该节点的子孙节点NIL的所有路径上包含相同数据的黑色节点。【注:这里指到叶子节点的路径。】
特别说明:
- 特性第三条指的叶子节点为空(NIL或NULL)的结点
- 特性第五条,确保没有一条路径会比其他路径长出两倍。因为红黑树是相对接近平衡二叉树的。
红黑树的应用:
红黑树可以用来存储有序数据,时间复杂度是O(logn),效率非常高。例如,Java集合中的TreeSet和TreeMap都是通过红黑树来实现的。
红黑树的基本操作——左旋和右旋:
红黑树在删除或者添加节点滞后,很有可能破坏原有的红黑树结构特性,这时候旋转操作就必不可少了,这和AVL树有一点点相像。总而言之,旋转的目的是为了保持红黑树的特性。
左旋

对节点F进行左旋,意味着将节点F变为其右孩子节点R的左孩子结点,并将节点R的左子树变为节点F的右子树。
右旋

对节点F进行右旋,意味着将节点F变为其左孩子节点L的右孩子节点,并将节点L的右子树变为节点F的左子树
二、二叉树的实现及遍历
1、用Java代码实现一个二叉树的创建
(1)创建一个二叉树的结点:
public static class TreeNode {
public int value;
public TreeNode left;
public TreeNode right;
public TreeNode(int value) {
this.value = value;
}
}(2)创建二叉树:
/**
* 创建二叉树
*
* @return
*/
public TreeNode createBinaryTree(LinkedList<Integer> linkedList) {
TreeNode treeNode = null;
if (linkedList == null || linkedList.size() == 0) return treeNode;
Integer value = linkedList.removeFirst();
if (value != null) {
treeNode = new TreeNode(value);
treeNode.left = createBinaryTree(linkedList);
treeNode.right = createBinaryTree(linkedList);
}
return treeNode;
}2、二叉树的遍历
(1)先序遍历:
/**
* 二叉树遍历-先序遍历
*
* @param treeNode
*/
public void preOderBinaryTree(TreeNode treeNode) {
if (treeNode == null) return;
System.out.println(treeNode.value);
preOderBinaryTree(treeNode.left);
preOderBinaryTree(treeNode.right);
}(2)中序遍历:
/**
* 二叉树遍历-中序遍历
*
* @param treeNode
*/
public void midOrderBinaryTree(TreeNode treeNode) {
if (treeNode == null) return;
midOrderBinaryTree(treeNode.left);
System.out.println(treeNode.value);
midOrderBinaryTree(treeNode.right);
}(3)后序遍历:
/**
* 二叉树遍历-后序遍历
*
* @param treeNode
*/
public void postOrderBinaryTree(TreeNode treeNode) {
if (treeNode == null) return;
postOrderBinaryTree(treeNode.left);
postOrderBinaryTree(treeNode.right);
System.out.println(treeNode.value);
}(4)层序遍历:
/**
* 二叉树遍历-层序遍历
*
* @param root
*/
public List<List<Integer>> levelOrderBinaryTree(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) return result;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int queueSize = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < queueSize; i++) {
TreeNode treeNode = queue.poll();
if (treeNode != null) level.add(treeNode.value);
if (treeNode != null && treeNode.left != null) {
queue.offer(treeNode.left);
}
if (treeNode != null && treeNode.right != null) {
queue.offer(treeNode.right);
}
}
result.add(level);
}
return result;
}(5)求二叉树的最大深度:
/**
* 求二叉树的最大深度
*
* @param root
* @return
*/
public int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}