1、关于矩阵的一些想法

        有小伙伴看到矩阵就脑瓜壳疼，那是没有了解数学家为啥闲的没事要用矩阵呢，从来没有人说不用矩阵就算不了，矩阵最初我认为是数学家偷懒，因为写一堆方程字太多太长，所以用了简写的形式，后来又有大佬发现简写后变成了一堆数字了，那是不是有啥规律呢，慢慢研究发展成了一门学科，当你方程组写多了时候，用矩阵运算真是方便啊。但是不管矩阵在怎么变，他也只能解决线性系统，什么是线性系统，即满足其次性又满足叠加性的系统。其实归根到底还是在解方程。入门教程有的线性系统大多是2元或者3元，初学者可能看不出来写成矩阵有啥优势，直接解方程组不香吗？但是实际应用中系统大多是3元以上，3元以解个方程组还勉强可以，那10元呢，20元呢，是不是就不香了。打破旧的思想桎梏，才能更上一层楼，多看几遍，复习复习概率和线性代数，卡尔曼滤波真没用啥高级技能。

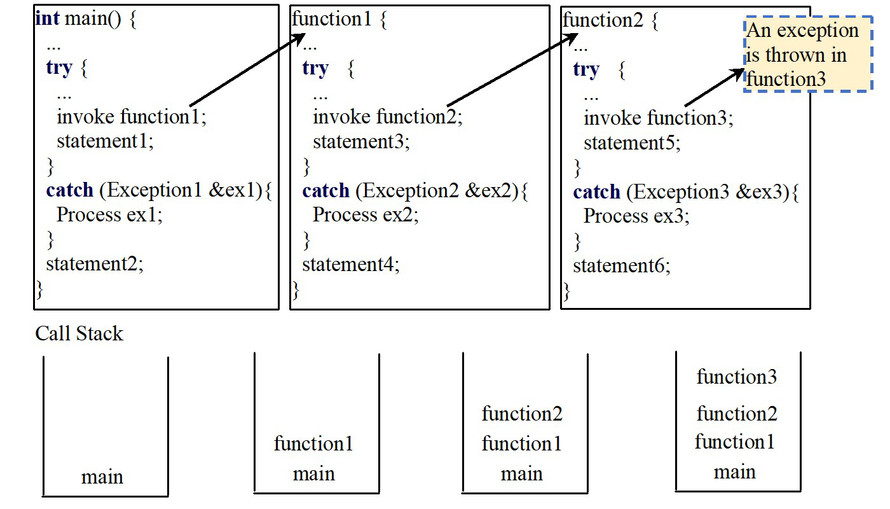
2、卡尔曼滤波原理简单理解

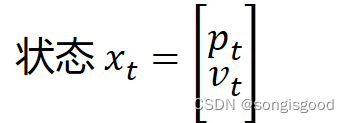
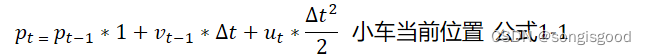
上述两个公式用于描述小车的状态方程，将该方程组转换成矩阵形式

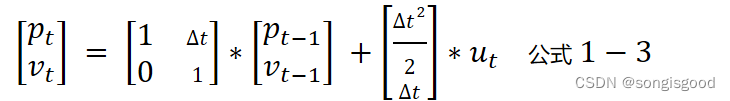
公式1-3可以写成矢量形式  (公式上面的尖冒号表示的是估计值不是真实值，减号表示有欠缺不是最好的)

 

Q表示预测噪声

 

观测矩阵

 

状态更新

 

噪声协方差矩阵的更新

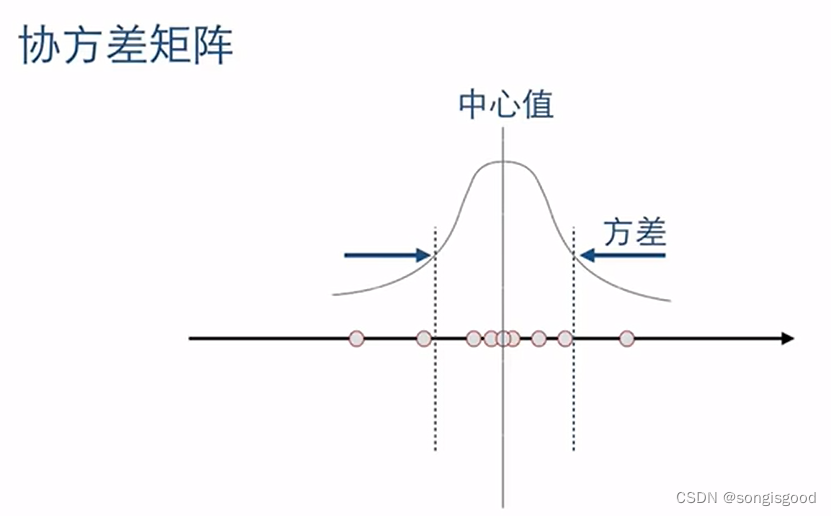
3、重要的总结

1、核心思想就是根据噪声协方差，计算相关加权值，核心思想看下一条。

2、反复迭代能收敛的原因是，噪声协方差满足高斯分布，状态矩阵噪声和观测矩阵噪声相乘就是最优估计的噪声矩阵 满足高斯分布，高斯分布的特性是两个高斯分布相乘产生的新高斯分布，新高斯函数的方差会小于任意相乘高斯函数的方差，看上图协方差矩阵。所以迭代一次方差比上一小，所以反复迭代，最终收敛到真实值附近。