一、题目

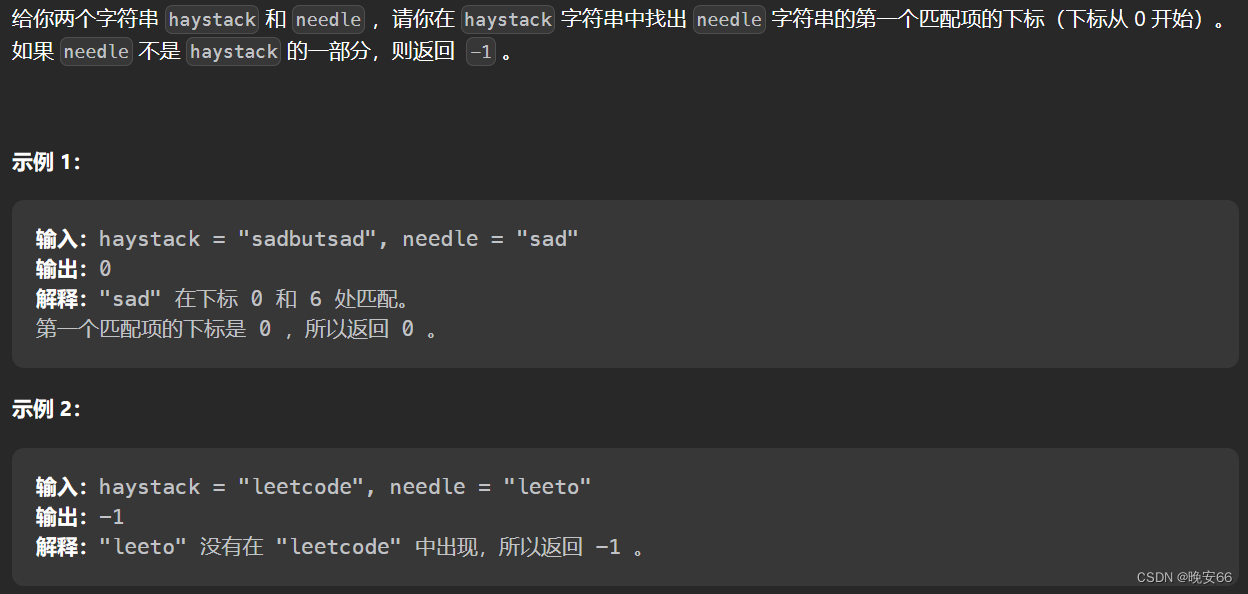
在这里插入图片描述

二、暴力穷解法

思路分析：首先判断字符串是否合法，然后利用for循环，取出子字符串利用compare函数进行比较。
程序如下：

class Solution {
public:
	// 复杂度n * m
	int strStr(string haystack, string needle) {
		if (haystack.size() < needle.size()) return -1;	
		if (!needle.size()) return 0; // needle为空返回0
		for (int i = 0; i < haystack.size(); ++i) {
			string substr = haystack.substr(i, needle.size());
			if (!needle.compare(substr)) return i;
		}
		return -1;
	}
};

复杂度分析：

时间复杂度： $O (n * m)$ ，假设haystack的长度为n，needle的长度为m，for循环的复杂度为n，当中调用了compare函数，它是逐字符比较的，复杂度为m，因此总复杂度为 $O (n * m)$ 。
空间复杂度： $O (1)$ 。

三、KMP算法

思路分析：这个算法比较著名了，简单来讲就是建立前缀表，然后进行匹配，匹配失败就根据前缀表找到下一个模式串的位置。具体的思路可以看看笔者的这片文章【算法与数据结构】字符串匹配算法。
程序如下：

	// KMP算法
    void getNext(int* next, const string& s) {
        int j = -1;
        next[0] = j;
        for (int i = 1; i < s.size(); i++) { // 注意i从1开始
            while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回退
            }
            if (s[i] == s[j + 1]) { // 找到相同的前后缀
                j++;
            }
            next[i] = j; // 将j（前缀的长度）赋给next[i]
            
        }
    }
    int strStr2(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int* next = new int[needle.size()];
        //int next[needle.size()]; 
        getNext(next, needle);
        //my_print(next, needle.size(), "前缀表：");
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while (j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // i的增加在for循环里
            }
            if (j == (needle.size() - 1)) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }

复杂度分析：

时间复杂度： $O (n + m)$ ，其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
空间复杂度： $O (m)$ ，需要额外的空间存放大小为m的数组。

四、Sunday算法

思路分析：思路部分大家也可以看笔者的这篇文章【算法与数据结构】字符串匹配算法。第二个版本的算法相对来说简洁快速一些。
程序如下：

    // Sunday算法
    int find_single_char(char c, const string& needle) {   
        for (int i = needle.size() - 1; i >= 0; --i) {  // 找最右端的字符，因此从后往前循环
            if (c == needle[i]) return i; 
        }
        return -1;
    }
    int strStr3(string haystack, string needle) {
        if (haystack.size() < needle.size()) return -1;     // 检查合法性
        if (!needle.size()) return 0;                       // needle为空返回0      
        for (int i = 0; i <= haystack.size() - needle.size(); ) {
            for (int j = 0; j < needle.size(); ++j) {
                if (needle[j] != haystack[i + j]) {     // 匹配失败                
                    int k = find_single_char(haystack[i + needle.size()], needle);   // 文本字符串末尾的下一位字符串
                    if (k == -1)   i += needle.size() + 1;  // 模式串向右移动 模式串长度 + 1 
                    else i += needle.size() - k;            // 向右移动 模式串最右端的该字符到末尾的距离+1
                    break;
                }     
                if (j == needle.size() - 1) return i;   // 匹配成功
            }
        }
        return -1;
    }

    // 查找算法用哈希表代替的Sunday算法   
    int strStr4(string haystack, string needle) {
        if (haystack.size() < needle.size()) return -1;     // 检查合法性
        if (!needle.size()) return 0;                       // needle为空返回0  

        int shift_table[128] = { 0 };       // 128为ASCII码表长度
        for (int i = 0; i < 128; i++) {     // 偏移表默认值设置为 模式串长度 + 1
            shift_table[i] = needle.size() + 1;
        }
        for (int i = 0; i < needle.size(); i++) {	// 如果有重复字符也会覆盖，确保shift_table是 模式串最右端的字符到末尾的距离 + 1
            shift_table[needle[i]] = needle.size() - i;
        }

        int s = 0; // 文本串初始位置
        // 模式串已经匹配到的位置
        int j;
        while (s <= haystack.size() - needle.size()) {
            j = 0;
            while (haystack[s + j] == needle[j]) { 
                ++j;
                if (j >= needle.size()) return s;   // 匹配成功
            }
            // 找到主串中当前跟模式串匹配的最末字符的下一个字符
            // 在模式串中出现最后的位置
            // 所需要从(模式串末尾+1)移动到该位置的步数
            s += shift_table[haystack[s + needle.size()]];
        }
        // 输出结果
        return -1;
    }

复杂度分析：

时间复杂度：平均时间复杂度为 $O (n)$ ，最坏情况时间复杂度为 $O (n * m)$ 。
空间复杂度： $O (1)$ 。

五、完整代码

# include <iostream>
# include <string>
using namespace std;

void my_print(int* arr, int arr_len, string str) {
    cout << str << endl;
    for (int i = 0; i < arr_len; ++i) {
        cout << arr[i] << ' ';
    }
    cout << endl;
}

class Solution {
public:
	// 暴力穷解
	// 复杂度n * m
	int strStr(string haystack, string needle) {
		if (haystack.size() < needle.size()) return -1;	
		if (!needle.size()) return 0; // needle为空返回0
		for (int i = 0; i < haystack.size(); ++i) {
			string substr = haystack.substr(i, needle.size());
			if (!needle.compare(substr)) return i;
		}
		return -1;
	}

	// KMP算法
    void getNext(int* next, const string& s) {
        int j = -1;
        next[0] = j;
        for (int i = 1; i < s.size(); i++) { // 注意i从1开始
            while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回退
            }
            if (s[i] == s[j + 1]) { // 找到相同的前后缀
                j++;
            }
            next[i] = j; // 将j（前缀的长度）赋给next[i]
            
        }
    }
    int strStr2(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int* next = new int[needle.size()];
        //int next[needle.size()]; 
        getNext(next, needle);
        //my_print(next, needle.size(), "前缀表：");
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while (j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // i的增加在for循环里
            }
            if (j == (needle.size() - 1)) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }

    // Sunday算法
    int find_single_char(char c, const string& needle) {   
        for (int i = needle.size() - 1; i >= 0; --i) {  // 找最右端的字符，因此从后往前循环
            if (c == needle[i]) return i; 
        }
        return -1;
    }
    int strStr3(string haystack, string needle) {
        if (haystack.size() < needle.size()) return -1;     // 检查合法性
        if (!needle.size()) return 0;                       // needle为空返回0      
        for (int i = 0; i <= haystack.size() - needle.size(); ) {
            for (int j = 0; j < needle.size(); ++j) {
                if (needle[j] != haystack[i + j]) {     // 匹配失败                
                    int k = find_single_char(haystack[i + needle.size()], needle);   // 文本字符串末尾的下一位字符串
                    if (k == -1)   i += needle.size() + 1;  // 模式串向右移动 模式串长度 + 1 
                    else i += needle.size() - k;            // 向右移动 模式串最右端的该字符到末尾的距离+1
                    break;
                }     
                if (j == needle.size() - 1) return i;   // 匹配成功
            }
        }
        return -1;
    }
};

int main()
{
	//string haystack = "sadbutsad";
	//string needle = "sad";
	//string haystack = "abc";
	//string needle = "c";
    //string haystack = "substring searching algorithm";
    //string needle = "search";
    //string haystack = "hello";
    //string needle = "ll";
    //string haystack = "mississippi";
    //string needle = "issi";
    string haystack = "aabaaaababaababaa";
    string needle = "bbbb";
	int k = 2;
	Solution s1;
	cout << "目标字符串：\n" << "“" << haystack << "”" << endl;
	int result = s1.strStr3(haystack, needle);
	cout << "查找子串结果：\n" << result << endl;
	system("pause");
	return 0;
}