博弈，思维，分类讨论

题意：

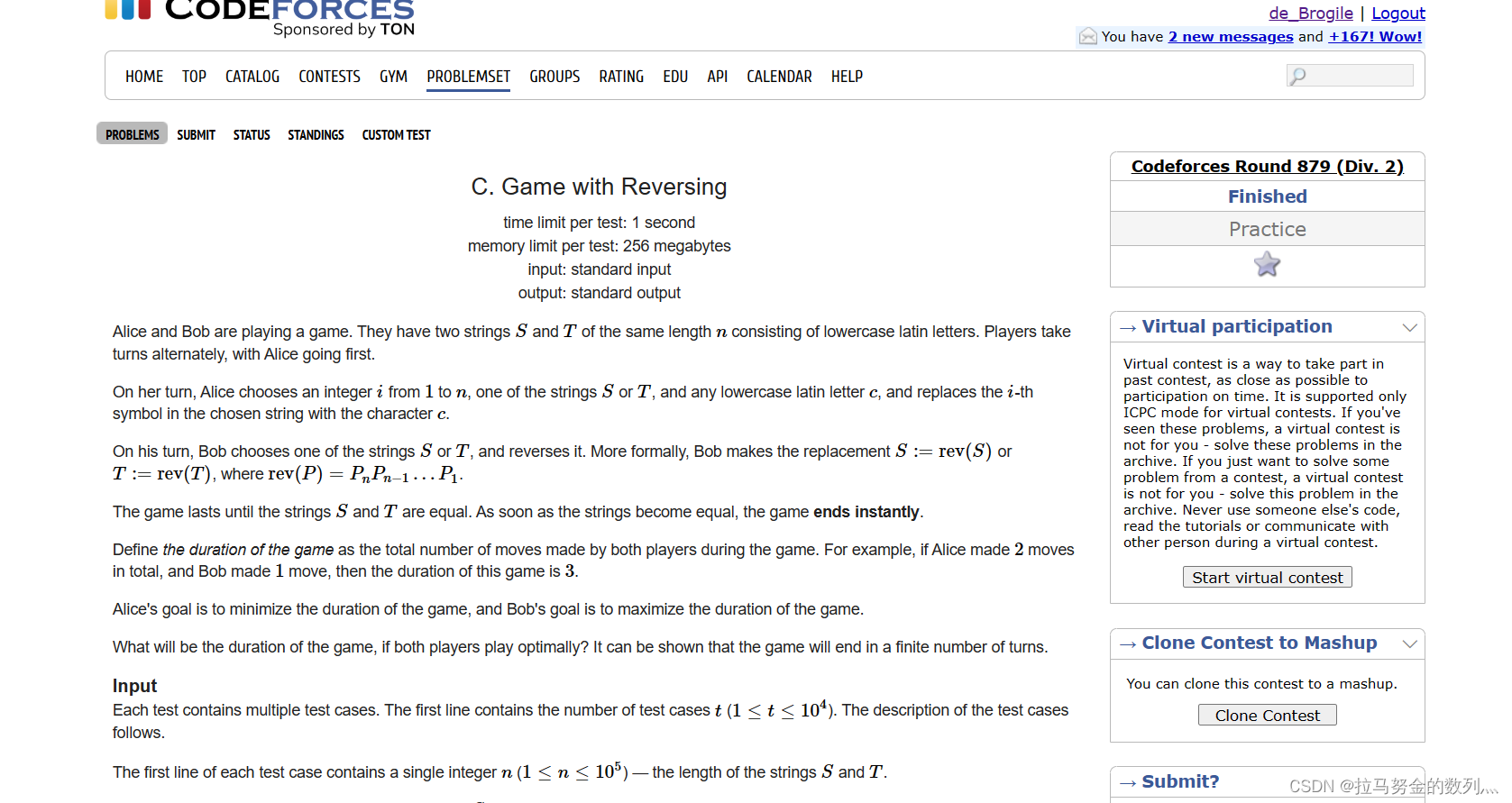
给你两个字符串，Alice可以每次选一个字符串的任意字母换成任意的字母，Bob可以选择一个字符串进行反转，Alice希望快速结束游戏，Bob希望拖延游戏，问你如果两者都是最优策略的情况下游戏时间是多少？

分析：

看题目发现 好像可以从Bob着手分析，首先反转一个字符串两次是不改变的

分奇偶来看，如果游戏结束时候 Bob进行了偶数次反转，容易想到 他不改变两个字符串的各个字母的索引顺序，当然有可能两个都是反着的

如果奇数次反转的话，那么肯定有一个字符串是逆序的（和开始的顺序比较的话）

因此 我们Alice可以采取以下策略：

 假设Bob最后偶数次反转 我们只需要统计S和T的diff为cnt，则答案就是2*cnt - cnt%2

同理假设Bob最后反转了奇数次，统计S和（T的逆序）的diff为cnt 答案就是2*cnt-(1-cnt%2)

两者我们取小者就行了

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
typedef long long ll;
int main()
{
	int T;
	cin>>T;
    
    string str1,str2;
    while(T--){
    	int len;
    	cin>>len;
    	cin>>str1>>str2;
    	
    	int cnt1=0,cnt2=0;
    	for(int i=0;i<len;i++)
    	 if(str1[i]!=str2[i])cnt1++;
    	
    	reverse(str2.begin(),str2.end());
    	
    	for(int i=0;i<len;i++)
    	 if(str1[i]!=str2[i])cnt2++;
    	 
    	 
        cnt1 = 2*cnt1-cnt1%2;
        
        if(cnt2==0)cnt2 = 2;
        else cnt2 = 2*cnt2-(1-cnt2%2);
        
        cout<<min(cnt1,cnt2)<<endl;
    	
    	
    	
    	
    }
	
	
}