个人简单笔记。
目录
闭散列
开散列
插入
删除
查找
改变
什么是哈希桶呢？这是一个解决哈希数据结构的一种解决方法，在STL中的unorder_map与unorder_set的底层结构就是使用它来实现的。
闭散列
首先我们知道，哈希映射表是依据数组下标数据的。
这时候然后如果来了映射值数据为0的数据，检测发现0位置已经被30占用，需要线性探测后面的空位置，就存入数据，这就叫做哈希冲突。
这样看似非常方便，但是有一个非常不好的地方那就是将其他位置给占用了，这样如果存储了其他数据连带一片的冲突产生：让我们看下图。
我们1将下标1的位置占用了，那么11、21、31使用了依次占用后面空间位置。进入进数据
映射1的数据他们的连带将2，3，4下标位置映射给占用了，导致22、3、14第一次映射位置就发生哈希冲突，并且这3个数据也占用了下标5、6、7位置，造成一大片哈希冲突，极其影响数据增删查改。所以我们的必须改变哈希结构，使用开散列的方法。
开散列
开散列又名哈希桶、开链法。
我们的数据存放的不再是单纯存放数据到数组中，还记得我们的链表吗？我们的哈希表中存放的就是一个一个的链表的头节点数据。
这时候我们再将数据存放入表中。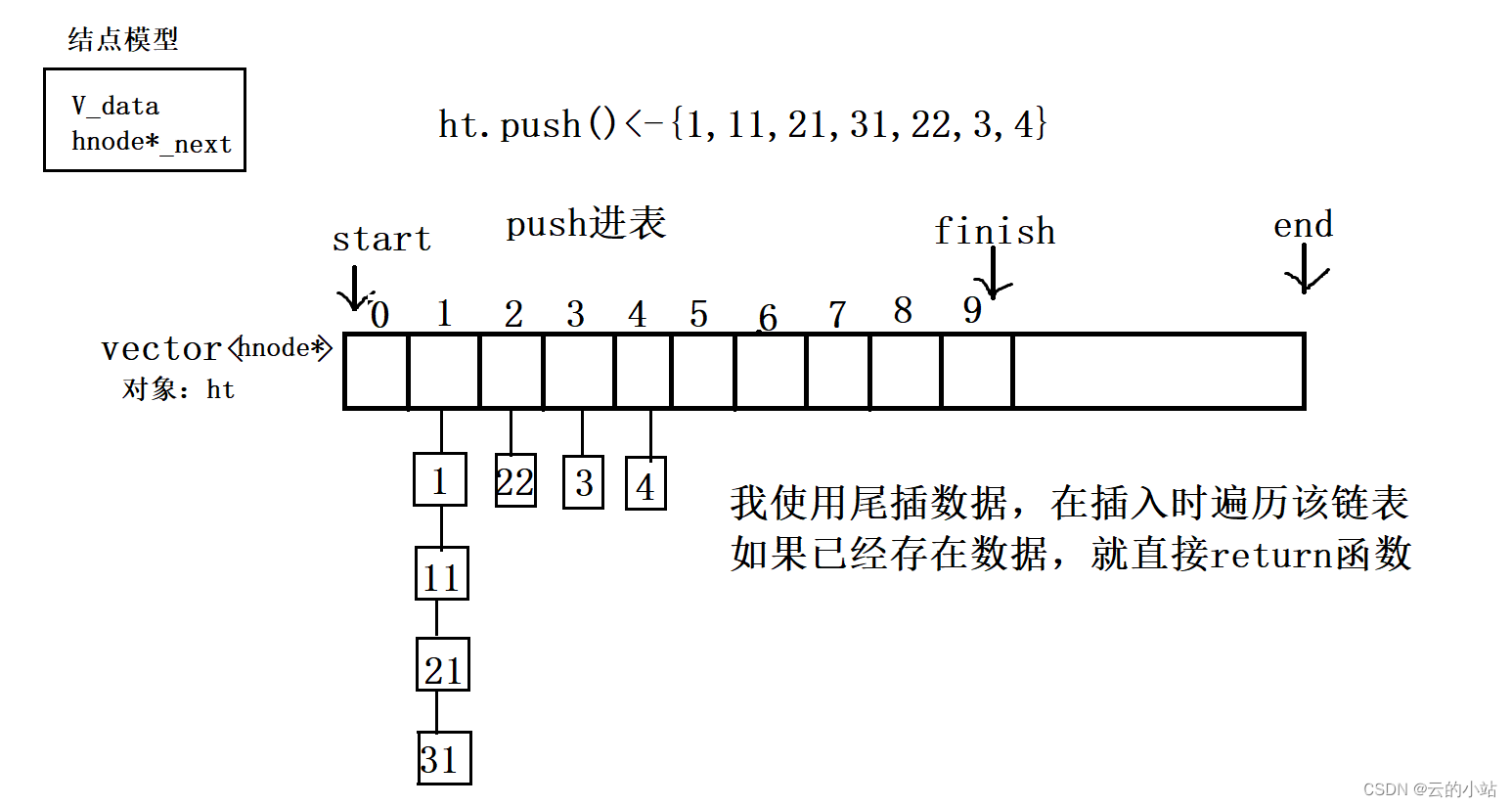
这时候映射到1的数据，自己冲突自己的，不影响其他下标位置，这就是我们的哈希桶模型。
插入
先映射寻找链表首端，再就是普通的链表插入。需要注意尾插的第一个插入或者头删的
bool insert(const pair<K, V>& kv)
{
//哈希桶的负载因子为1
if (_size + 1 > _tables.size())
{
//扩容逻辑
Hash hash;
size_t newsize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*>newTables;//我们的开散列不能去像闭散列一样创建新对象插入，
//我们需要的是重新创建的是数组表，将一个个node
//重新链接到新数组表中，避免需要一直重新创建结点。
newTables.resize(newsize);
//old表node移动到new表
//为了不浪费
for (size_t i = 0; i < _tables.size(); ++i)
{
Node* cur = _tables[i];//原表的每个元素都给cur
while (cur)
{
Node* oldnext = cur->_next;//记录原表当前结点的下一个
size_t index = hash(cur->_kv.first) % newTables.size();
cur->_next = newTables[index];//这里采用的是头插。
newTables[index] = cur;
cur = oldnext;//迭代
}
_tables[i] = nullptr;//置空原表，没必要但是好习惯
}
newTables.swap(_tables);//交换old与new表，完成扩容
}
Hash hash;//仿函数
size_t index = hash(kv.first) % (_tables.size());
//头插
if (Find(kv.first))
{
return false;
}
Node* newnode = new Node(kv);
newnode->_next = _tables[index];
_tables[index] = newnode;
//尾插
/*Node* newnode = new Node(kv);
if (_tables[index] == nullptr)
{
_tables[index] = newnode;
}
else
{
Node* cur = _tables[index];
Node*prev = _tables[index];
while (cur)
{
if (cur->_kv == kv)
{
delete newnode;//如果发现已经存在我们需要delete新结点，防止内存泄漏
return false;
}
prev = cur;
cur = cur->_next;
}
prev->_next = newnode;
}*/
_size++;//数据加一
return true;
}删除
bool Erese(const K& key)
{
if (_tables.size() == 0)//防止除0
{
return false;
}
Hash hash;
size_t index = hash(key) % (_tables.size());
Node* cur = _tables[index];//简单的链表删除
Node* prev = cur;
while (cur)
{
if (cur->_kv.first == key)
{
if (cur == _tables[index])//如果就是删除链表头结点
{
_tables[index] = cur->_next;
}
else//非头节点删除
{
prev->_next = cur->_next;
}
delete cur;
_size--;
return true;
}
prev = cur;//迭代
cur = cur->_next;
}
return false;
}查找
Node* Find(const K& key)
{
if (_tables.size() == 0)//防止除0
{
return nullptr;
}
Hash hash;
size_t index = hash(key) % (_tables.size());//找头节点位置
Node* cur = _tables[index];//普通的单链表查找
while (cur)
{
if (cur->_kv.first == key)//找到了
{
return cur;
}
cur = cur->_next;
}
return nullptr;//没找到
}改变
bool change(const K& key, const V& val)
{
Node* ret = Find(key);//查找位置
if (!ret)//没找到返回
{
return false;
}
else//找到改变返回
{
ret->_kv.second = val;
return true;
}
}
