1.概率论学习中的重难点

概率论是研究随机现象的数学分支，它的核心概念和重难点包括以下几点：

概率：概率是对事件发生可能性大小的度量，它通常用一个实数来表示。概率可以分为确定性概率和随机概率。
概率分布：概率分布是描述随机变量取值概率的图形表示。常见的概率分布有正态分布、二项分布、泊松分布、均匀分布等。
条件概率与边缘概率：条件概率是已知某事件发生的情况下，另一事件发生的概率。边缘概率则是在给定样本空间下，随机变量取特定值的概率。
独立性与相关性：独立性是指随机变量之间互不影响；相关性是指两个随机变量之间存在某种联系。
大数定律与中心极限定理：大数定律是描述当实验次数足够多时，随机变量的平均值收敛到其期望值；中心极限定理是指当样本量足够大时，大量独立随机变量的平均值趋于正态分布。
随机过程：随机过程是一种描述随机现象在时间域或空间域中变化的数学模型。常见的随机过程有马尔可夫链、平稳随机过程、布朗运动等。
独立试验与大数定律：独立试验是指在一个相同的条件下进行多次重复试验；大数定律是指在一个独立试验中，大量重复试验的平均结果会接近于期望值。
概率论的应用：概率论在金融、工程、物理、生物等领域有广泛的应用，如统计推断、风险评估、蒙特卡洛模拟等。

2.主要工具介绍

数学建模的学习通常涉及到大量的计算和处理数据，因此，概率论的学习可以从以下几个主流工具开始：

1. Python

Python是一种广泛使用的编程语言，它的语法简单、易于学习，且有大量的科学计算库可供使用，如Numpy、Pandas、Scikit-learn等。这些库可以帮助你处理、计算数据，并执行各种概率论相关的计算。

2. MATLAB

MATLAB是一种用于数值计算的编程语言和交互式环境，适合进行各种数学建模和分析。MATLAB的内置数学函数和统计工具箱可以用于概率论的学习。

3. R

R是一种用于统计计算和图形的编程语言和操作环境。R提供了许多统计和计算工具，以及大量的统计学和机器学习库，如ggplot2、tidyverse等，这些库可以用于概率论的学习和实践。

4. Octave

Octave是一种类似于MATLAB的编程语言和交互式环境，它提供了大量的数学函数和统计工具，可以用于概率论的学习。

5. Microsoft Excel

虽然Excel本身不是专门的数学建模软件，但它可以作为一个简单的数据分析和概率论计算工具。在Excel中，你可以使用内置的数据分析功能，进行各种概率论计算和分析。

6. 统计软件

如SPSS、Stata、Minitab等，也可以用于概率论的学习和实践。这些软件提供了大量的统计和计算工具，可以帮助你分析数据和执行各种概率论计算。
总之，学习概率论的过程中，可以使用多种工具进行实践和应用。根据你的编程背景、数据处理能力和实际需求，选择合适的工具进行学习和实践。

我将用Python、R和Excel为主要线索来开展本系列的学习。

3.理论内容概览（前两点）

1. 概率

在这里插入图片描述

确定性概率和随机概率的定义
确定性概率是指，如果一个事件在给定条件下发生的可能性是确定的，那么这个事件的概率就可以被认为是确定性概率。在某些情况下，我们可以准确地计算确定性概率。
随机概率是指，一个事件在给定条件下发生的可能性是随机的。这意味着我们无法准确预测一个事件在给定条件下发生的概率。随机概率通常使用概率分布或概率模型来表示。
确定性概率和随机概率的异同点
相同点：
• 它们都描述了事件发生的可能性。
• 它们都可以用于预测未来事件的可能结果。
• 它们都可以用来评估风险和不确定性。
• 它们都可以用于决策和预测分析。
不同点：
• 确定性概率可以通过计算得出，而随机概率是无法确定的。
• 确定性概率适用于有限数量的可能结果，而随机概率适用于无限数量的可能结果。
• 确定性概率的分布是已知的，而随机概率的分布是未知的。
• 确定性概率可以用于确定未来事件的结果，而随机概率仅能用于估计未来事件的可能性。
总之，确定性概率和随机概率的主要区别在于其概率的可计算性和不可预测性。确定性概率可以通过计算得出，而随机概率是无法确定的。确定性概率适用于有限数量的可能结果，而随机概率适用于无限数量的可能结果。

2. 概率分布

概率分布：概率分布是描述随机变量取值概率的图形表示。常见的概率分布有正态分布、二项分布、泊松分布、均匀分布等。
在这里插入图片描述

正态分布（Normal Distribution）的定义与性质：
正态分布的概率密度函数为：f(x) = (1/σ) * exp(-(x - μ)^2 / (2σ^2))，其中，μ为均值，σ为方差。
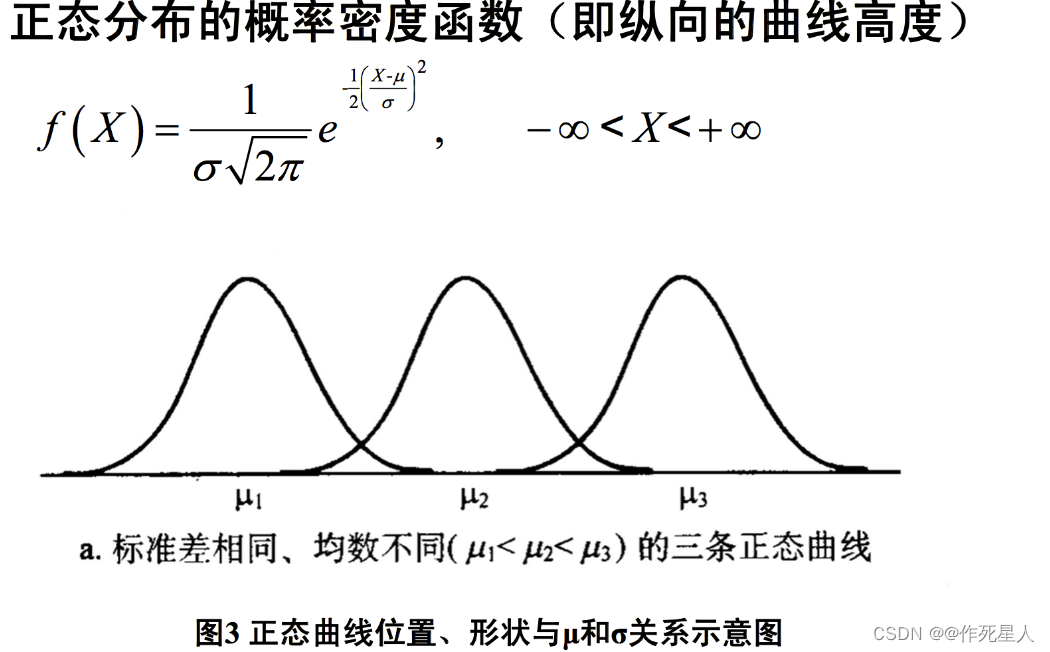
在这里插入图片描述

正态分布具有许多性质，包括以下几点：

正态分布的曲线呈钟形，两头低、中间高，左右对称，曲线下的面积为1。
正态分布的期望（均值）μ和标准差σ决定了分布的位置。μ决定分布的中心，σ决定分布的宽度。
正态分布的概率密度函数在正负1的位置取得峰值，因此μ=1和μ=-1处的概率密度为0。
正态分布的累积分布函数（CDF）为：f(x) = 1 - (1 - μ)^(1/σ)。
对于任意实数x，都有p(x) <= (1 - μ)^(1/σ)，其中p(x)表示在x处的概率密度值。

二项分布（Binomial Distribution）的定义与性质：
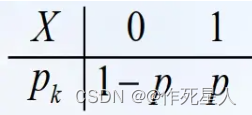
在这里插入图片描述

二项分布的概率密度函数为：f(x) = p * (1 - p)^n * e^(-x2/n)，其中，n为试验次数，p为成功概率。二项分布具有以下性质：

二项分布在n次独立重复试验中成功k次的概率是固定的，可以通过二项分布概率质量函数（PMF）计算：p(k) = C(n, k)* (1 - p)^(n - k)。
二项分布的累积分布函数（CDF）为：f(x) = p* e^(-x2/n)。

泊松分布（Poisson Distribution）的定义与性质：
泊松分布的概率密度函数为：f(x) = λ * e^(-λ/σ)，其中，λ为事件发生的平均值，σ为事件的标准差。
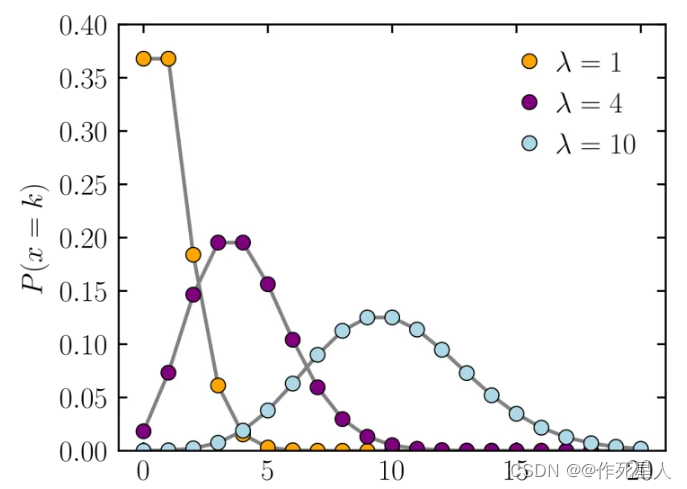
在这里插入图片描述

泊松分布具有以下性质：

泊松分布在平均发生时间间隔固定的情况下，统计某个时间段内发生某事件的次数。
泊松分布的累积分布函数（CDF）为：f(x) = 1 - e^(-λ/σ)。
泊松分布与正态分布的关系：当λ = μ=1时，泊松分布退化为正态分布。

均匀分布（Uniform Distribution）的定义与性质：
均匀分布的概率密度函数为：f(x) = (a - b) / (b - a)，其中，a <= x <= b。
在这里插入图片描述

均匀分布具有以下性质：
均匀分布在一定的区间范围内取值的概率相等。
均匀分布的累积分布函数（CDF）为：f(x) = (1 - f(x)) / (b - a)。

举例说明：

正态分布的例子：假设某公司员工的平均工资为5000元，标准差为1000元。从该公司随机抽取3名员工，计算这3名员工的平均工资。这个问题符合正态分布，可以通过正态分布概率密度函数计算概率，并使用正态分布的累积分布函数计算概率密度值。
二项分布的例子：假设在一个独立重复试验中，成功概率为0.5。在100次独立重复试验中，求成功50次的次数。这个问题符合二项分布，可以通过二项分布概率质量函数（PMF）计算概率。
泊松分布的例子：假设在一个停车场，平均每小时有10辆汽车驶入。每辆汽车驶入停车场的时间间隔都是相等的，求平均每小时驶入停车场5辆汽车的概率。这个问题符合泊松分布，可以通过泊松分布概率密度函数计算概率。
均匀分布的例子：假设在一个盒子中放有10个红球和10个白球，每次摸到红球的概率为1/3。求在2次摸球中，至少摸到1个白球的概率。这个问题符合均匀分布，可以通过均匀分布概率密度函数计算概率。

下章预告：
5. 条件概率与边缘概率
4. 独立性与相关性
6. 大数定律与中心极限定理
7. 随机过程
8. 独立试验与大数定律
9. 概率论的应用