6909.最长奇偶子数组（双指针）

给你一个下标从 0 开始的整数数组 nums 和一个整数 threshold 。

请你从 nums 的子数组中找出以下标 l 开头、下标 r 结尾 (0 <= l <= r < nums.length) 且满足以下条件的 最长子数组 ：

• nums[l] % 2 == 0
• 对于范围 [l, r - 1] 内的所有下标 i ，nums[i] % 2 != nums[i + 1] % 2
• 对于范围 [l, r] 内的所有下标 i ，nums[i] <= threshold

以整数形式返回满足题目要求的最长子数组的长度。

注意：子数组 是数组中的一个连续非空元素序列。

示例 1：

输入：nums = [3,2,5,4], threshold = 5
输出：3
解释：在这个示例中，我们选择从 l = 1 开始、到 r = 3 结束的子数组 => [2,5,4] ，满足上述条件。
因此，答案就是这个子数组的长度 3 。可以证明 3 是满足题目要求的最大长度。

示例 2：

输入：nums = [1,2], threshold = 2
输出：1
解释：
在这个示例中，我们选择从 l = 1 开始、到 r = 1 结束的子数组 => [2] 。
该子数组满足上述全部条件。可以证明 1 是满足题目要求的最大长度。

示例 3：

输入：nums = [2,3,4,5], threshold = 4
输出：3
解释：
在这个示例中，我们选择从 l = 0 开始、到 r = 2 结束的子数组 => [2,3,4] 。 
该子数组满足上述全部条件。
因此，答案就是这个子数组的长度 3 。可以证明 3 是满足题目要求的最大长度。

提示：

• 1 <= nums.length <= 100
• 1 <= nums[i] <= 100
• 1 <= threshold <= 100

思路

这道题目可以使用滑动窗口的思路，但更准确的说是一个双指针的策略。

对于这种类型的问题，我们通常会有一个左指针和一个右指针。左指针表示子数组的开始，右指针表示子数组的结束。

我们会尝试将右指针向右移动来增大子数组，直到子数组不再满足要求。然后，我们会移动左指针，跳过不满足条件的元素，再尝试扩大子数组。

完整版

class Solution {
public:
    int longestAlternatingSubarray(vector<int>& nums, int threshold) {
    int max_len = 0, len = 0, n = nums.size();
    for (int i = 0; i < n; ) {
        // 如果当前元素为偶数且小于等于阈值
        if (nums[i] % 2 == 0 && nums[i] <= threshold) {
            len = 1;
            // 向后查找满足条件的子数组
            while (i + 1 < n && nums[i] % 2 != nums[i + 1] % 2 && nums[i + 1] <= threshold) {
                len++;
                i++;
            }
            // 更新最大长度
            max_len = max(max_len, len);
        }
        i++;
    }
    return max_len;
    }
};

6916.和等于目标的质数对（质数判断，重要）

给你一个整数 n 。如果两个整数 x 和 y 满足下述条件，则认为二者形成一个质数对：

• 1 <= x <= y <= n
• x + y == n
• x 和 y 都是质数

请你以二维有序列表的形式返回符合题目要求的所有 [xi, yi] ，列表需要按 xi 的 非递减顺序 排序。如果不存在符合要求的质数对，则返回一个空数组。

**注意：**质数是大于 1 的自然数，并且只有两个因子，即它本身和 1 。

示例 1：

输入：n = 10
输出：[[3,7],[5,5]]
解释：在这个例子中，存在满足条件的两个质数对。 
这两个质数对分别是 [3,7] 和 [5,5]，按照题面描述中的方式排序后返回。

示例 2：

输入：n = 2
输出：[]
解释：可以证明不存在和为 2 的质数对，所以返回一个空数组。 

提示：

• 1 <= n <= 10^6

思路

本题思路就是遍历从2到n / 2的所有数，并检查了i和n - i是否都是质数。

但是，判断一个数是否为质数的操作不是通过暴力方法实现的。

在这里，我们使用了一种叫做"埃拉托斯特尼筛法"（Sieve of Eratosthenes）的算法预先计算出了小于等于n的所有数是否为质数，然后在查找质数对时，可以直接查找is_prime数组，而无需再次检查每个数是否为质数。这大大提高了效率。

质数判断：埃拉托斯特尼筛法获取所有小于等于n的质数

博客整理：埃氏筛法找质数

// 使用埃拉托斯特尼筛法找出所有小于等于n的质数
// 从2开始，对于每一个i，如果i是质数，那么i的所有倍数都不是质数
// 只需要检查到 sqrt(n) ，因为如果 n 不是质数，那么它必定有一个小于等于 sqrt(n) 的因子
for (int i = 2; i * i <= n; ++i) {
   if (is_prime[i]) {
   //此处也可以i*i，是一种优化
      for (int j = i * 2; j <= n; j += i) {
          is_prime[j] = false;
       }
   }
}

这个算法用于求解小于或等于n的所有质数。

算法的基本思想是，首先假设2至n之间的所有数字都是质数，然后从2开始，将所有2的倍数标记为非质数；接下来找到下一个未被标记的数字，并将其所有的倍数标记为非质数，依次类推，直到遍历到√n。遍历结束后，所有未被标记为非质数的数字就是我们要找的质数。

这个算法的时间复杂度是O(n log log n)。

具体来说，这个算法的时间复杂度的推导方法是，首先，对于每一个质数p，我们需要将数组中所有p的倍数标记为非质数。标记操作的次数为n/p。而所有这样的p的和大约为n log log n（这是基于素数定理的推导结果）。因此，总的操作次数约为n log log n。

至于空间复杂度，如果我们使用一个长度为n+1的布尔数组来记录每一个数是否为质数，那么空间复杂度为O(n)。

质数定义

质数是一个自然数，且除了1和它本身以外没有其他因数。换句话说，如果一个数大于1，且只有两个正因数（1和它本身），那么它就是一个质数。例如，2、3、5、7、11、13等都是质数。注意，1和0不是质数。

根据质数的定义，质数p的倍数必然有其他因数（至少包括p本身），所以它们不可能是质数。因此，我们在使用埃拉托斯特尼筛法求质数时，对于每一个已知的质数p，都需要将所有p的倍数标记为非质数。

例如，当p=2时，我们将所有2的倍数（即所有偶数）标记为非质数。然后，找到下一个还未被标记为非质数的数（即3），将所有3的倍数标记为非质数，以此类推。这样，剩下的未被标记的数就都是质数了。

完整版

• 这种解法通过预先计算的方法将查找质数的复杂度从O(sqrt(n))降低到了O(1)，并且只需要遍历一次就可以找到所有满足条件的质数对

class Solution {
public:
    vector<vector<int>> findPrimePairs(int n){
        // 建立一个长度为 n+1 的布尔向量 is_prime，并将所有元素初始化为 true
        vector<bool> is_prime(n + 1, true);

        // 0和1不是质数，所以我们将它们标记为 false
        is_prime[0] = is_prime[1] = false;

        // 使用埃拉托斯特尼筛法找出所有小于等于n的质数
        // 从2开始，对于每一个i，如果i是质数，那么i的所有倍数都不是质数
        // 只需要检查到 sqrt(n) ，因为如果 n 不是质数，那么它必定有一个小于等于 sqrt(n) 的因子
        for (int i = 2; i * i <= n; ++i) {
            if (is_prime[i]) {
                for (int j = i * i; j <= n; j += i) {
                    is_prime[j] = false;
                }
            }
        }

        vector<vector<int>> result; // 用于保存结果的向量

        // 从2遍历到n/2，检查i和n-i是否都是质数
        // 只需要遍历到n/2，因为对于大于n/2的x，y一定小于x，这不满足x <= y的条件
        for (int i = 2; i <= n / 2; ++i) {
            if (is_prime[i] && is_prime[n - i]) {
                result.push_back({i, n - i}); // 如果i和n-i都是质数，将它们添加到结果中
            }
        }
        return result; // 返回结果
    }        
};

为什么只遍历到n/2？

这是因为题目最初的要求是：

• 1 <= x <= y <= n
• x + y == n

我们在寻找的是两个数的对x和y（也就是i和n-i），满足它们的和为n。并且要求1 <= x <= y <= n，即y不应该小于x，那么当x大于n/2时，y一定会会小于x！

因此，在对第一个数字x进行遍历的时候，我们只需要遍历到n/2就可以了。

因为两数字和为n的情况下，比较小的那个数字范围一定<=n/2。

时间复杂度

这个算法的时间复杂度主要由两部分决定：

1. 埃拉托斯特尼筛法的部分：这个部分的时间复杂度是O(n log log n)。这是因为在计算质数的时候，我们首先从2开始，然后找出2的所有倍数并将它们标记为非质数。然后，我们找到下一个仍然被标记为质数的数（在这个例子中是3），并找出3的所有倍数并将它们标记为非质数。我们继续这个过程，直到我们已经检查了所有小于等于sqrt(n)的数。由于每个数只被标记一次，所以总的操作次数是n/2+n/3+n/5+…，这个级数的和近似为n log log n。
2. 查找质数对的部分：这个部分的时间复杂度是O(n)。这是因为我们只遍历一次从2到n/2的所有数，对于每个数i，我们查看i和n-i是否都是质数。数组查询不需要再遍历一遍数组，数组查询的时间复杂度是O(1)

补充：数组/哈希表查询操作时间复杂度

数组和哈希表（在最佳情况下）的查询时间复杂度都是O(1)。

在数组中，你可以直接通过索引访问元素。所以不论数组有多大，访问其元素的时间都是常量，即O(1)。

在哈希表中，元素的存储位置是通过元素的键经过哈希函数计算得到的。所以理想情况下，通过键来查找元素的时间复杂度也是O(1)。但是，实际情况可能会复杂一些，因为哈希表可能会出现碰撞（两个不同的键经过哈希函数得到同一个位置），这时就需要额外的时间来解决冲突。但在哈希函数选择合适，且哈希表大小足够大的情况下，哈希表的查找时间复杂度一般可以近似为O(1)。

但请注意，这里说的是“查询”操作的时间复杂度，如果是插入、删除操作，对于数组和哈希表的时间复杂度可能就不一样了。

6911.不间断子数组（双指针滑动窗口）

• 本题也算是滑动窗口的典型题，滑动窗口的核心在于连续！如果需要得到的结果是满足某种条件的连续的子数组，可以考虑使用滑动窗口来做！

给你一个下标从 0 开始的整数数组 nums 。nums 的一个子数组如果满足以下条件，那么它是 不间断 的：

• i，i + 1 ，…，j 表示子数组中的下标。对于所有满足 i <= i1, i2 <= j 的下标对，都有 0 <= |nums[i1] - nums[i2]| <= 2 。

请你返回 不间断 子数组的总数目。

子数组是一个数组中一段连续 非空 的元素序列。

示例 1：

输入：nums = [5,4,2,4]
输出：8
解释：
大小为 1 的不间断子数组：[5], [4], [2], [4] 。
大小为 2 的不间断子数组：[5,4], [4,2], [2,4] 。
大小为 3 的不间断子数组：[4,2,4] 。
没有大小为 4 的不间断子数组。
不间断子数组的总数目为 4 + 3 + 1 = 8 。
除了这些以外，没有别的不间断子数组。

示例 2：

输入：nums = [1,2,3]
输出：6
解释：
大小为 1 的不间断子数组：[1], [2], [3] 。
大小为 2 的不间断子数组：[1,2], [2,3] 。
大小为 3 的不间断子数组：[1,2,3] 。
不间断子数组的总数目为 3 + 2 + 1 = 6 。

提示：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9

思路

这道题目也是一道典型的滑动窗口题，要求找出所有满足特定条件的连续子数组的个数。特定条件是，对于子数组中的任意两个元素，他们的绝对值差不能超过 2。

统计符合条件的连续子数组个数，关键的思想在于，我们一直保持一个满足条件的窗口，然后看看有多少个子数组符合条件。因为原题目中，要求的是子数组任意两个元素绝对值差不超过2。因此，我们就需要知道子数组的最大元素和最小元素之间的差值。

为了节省时间复杂度，防止我们每次找最大值和最小值都需要重新遍历，本题我们最好采用可重复的有序哈希表multiset/multimap来实现。

因为本题nums是存在重复元素的！因此我们只能选取key可重复的哈希表，允许重复的哈希表只有multiset和multimap。因为并不涉及次数统计，所以采用multiset。

这里补充一下set和map的基本常识：

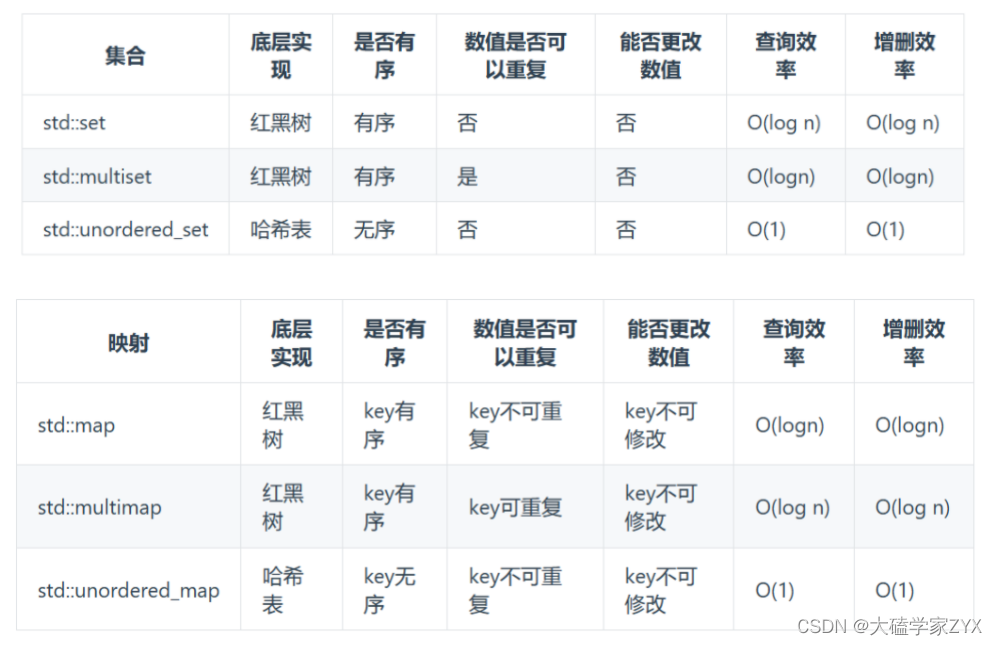
本题采用哈希表的目的，就是为了避免子数组本身找最大值和最小值造成的时间复杂度。如果用数组，数组是不存在哈希表这样自动排序，直接找到最大值和最小值的机制的。

我们可以用一个set来存储窗口中的元素，然后使用两个指针i和j来表示窗口的两端。本题特定条件是子数组任意两数绝对值差<=2，而哈希表本身自带排序，因此也不需要单独写条件判断函数。

双指针滑动窗口做法

class Solution {
public:
    long long continuousSubarrays(vector<int> &nums) {
        long long ans = 0;
        multiset<int> s;
        int left = 0;
        for (int right = 0; right < nums.size(); right++) {
            s.insert(nums[right]);
            while (*s.rbegin() - *s.begin() > 2){
                //find是找值相同的元素，而不是找下标
                s.erase(s.find(nums[left]));
                left++;
            }
            ans += right - left + 1;
        }
        return ans;
    }
};

multiset 是一种可以自动排序并且可以包含重复元素的集合。我们使用 multiset 来存储窗口中的元素，然后使用 *s.rbegin() 和 *s.begin() 来得到窗口中的最大元素和最小元素。

如何返回set中最小元素和最大元素：*s.rbegin()

std::multiset 和 std::multimap 默认都是按照键值的升序排列的，这一点和 std::sort 函数的默认排序顺序（也是升序）是一样的。

set中， s.begin() 实际上指向的是最小的元素，而 s.rbegin() 指向的是最大的元素。

为什么最大元素不是*s.end()

对于 std::multiset 和 std::multimap 这类容器，s.end() 并不指向最后一个元素，而是指向最后一个元素之后的“位置”。这是因为在 C++ 中，范围是左闭右开的，即包括起始位置，但不包括终止位置。因此，如果使用 *s.end() 来尝试访问元素，实际上会出现未定义行为。

相反，s.rbegin() 返回的是一个反向迭代器，它指向的是容器中的最后一个元素。反向迭代器的工作方式和普通迭代器正好相反：递增反向迭代器会移动到前一个元素，递减反向迭代器会移动到后一个元素。因此，s.rbegin() 实际上给了我们一个方便的方式来访问容器中的最后一个元素。

在 C++ 中，s.begin() 和 s.rbegin() 分别返回指向 multiset 中最小元素和最大元素的迭代器。因为这些方法返回的是迭代器，所以我们需要使用 * 操作符来解引用迭代器，得到它们实际指向的值。

关于STL相关内容的补充：(2条消息) STL补充：STL中遵循的左闭右开原则/STL随机访问_大磕学家ZYX的博客-CSDN博客

如何获得窗口内所有大小的所有子数组

因为本题需要输出所有大小的数组个数，加上是遍历right，因此我们的策略是对于每一个right，找到右端点为right的所有大小的子数组！

例如[1,2,3]，所有以right=3为右端点的子数组，就是[1,2,3][2,3],[3]

也就是说，对于每一个right，[left,right]内包括所有大小的，以right为右端点的数组个数，是right-left+1。

因此result会在每一个right遍历的时候进行累加，得到**[left,right]窗口内所有大小的数组个数**。

单调队列做法

• 这种写法通过维护一个滑动窗口，以及两个双端队列 minQueue 和 maxQueue 来记录窗口中的最小值和最大值的位置。滑动窗口内的元素满足题目给出的条件，因此每次窗口向右滑动，都将 right - left + 1 加入到答案中。

class Solution {
public:
    long long continuousSubarrays(vector<int>& nums) {
        int n = nums.size();  // 获取数组长度
        deque<int> minQueue, maxQueue;  // 定义两个双端队列，用于存储滑动窗口内的最小值和最大值的位置
        long long ans = 0;  // 初始化答案为 0
        int left = 0;  // 初始化滑动窗口的左边界

        // 开始滑动窗口
        for (int right = 0; right < n; ++right) {
            // 维护 minQueue，使其始终从头到尾按照 nums[i] 的值递增
            while (!minQueue.empty() && nums[minQueue.back()] > nums[right]) {
                minQueue.pop_back();
            }
            // 维护 maxQueue，使其始终从头到尾按照 nums[i] 的值递减
            while (!maxQueue.empty() && nums[maxQueue.back()] < nums[right]) {
                maxQueue.pop_back();
            }

            // 将当前元素的位置加入两个队列
            minQueue.push_back(right);
            maxQueue.push_back(right);

            // 调整滑动窗口的左边界，使得窗口内的最大值和最小值之差不大于 2
            while (nums[maxQueue.front()] - nums[minQueue.front()] > 2) {
                if (minQueue.front() < maxQueue.front()) {
                    left = minQueue.front() + 1;
                    minQueue.pop_front();
                } else {
                    left = maxQueue.front() + 1;
                    maxQueue.pop_front();
                }
            }

            // 将滑动窗口的大小（即满足条件的连续子数组的数量）加入答案
            ans += right - left + 1;
        }

        return ans;  // 返回答案
    }
};