1. 图的遍历

给定一个图 G 和其中任意一个顶点 v0 ，从 v0 出发，沿着图中各边访问图中的所有顶点，且每个顶

点仅被遍历一次 。 " 遍历 " 即对结点进行某种操作的意思 。

请思考树以前是怎么遍历的，此处可以直接用来遍历图吗？为什么？

1.1 图的广度优先遍历

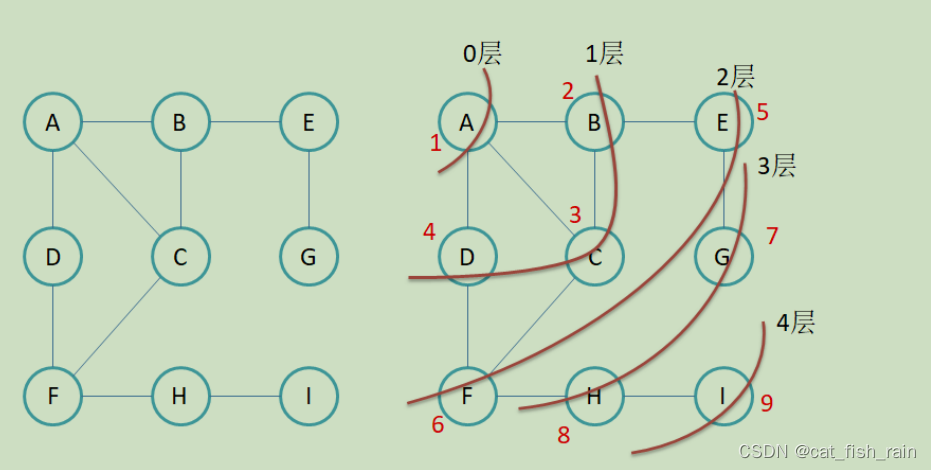
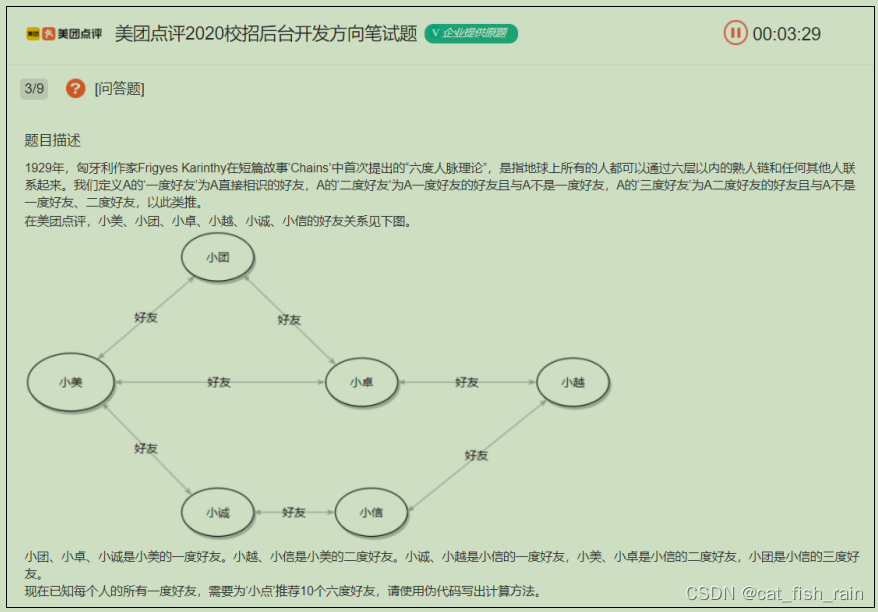
问题：如何防止节点被重复遍历

#include <iostream>
#include <vector>
#include<queue>
#include <map>
#include <algorithm>
using namespace std;

namespace LinkTable
{

    template <class W>
    struct LinkEgde
    {
        int _srcIndex;
        int _dstIndex;
        W _w;
        LinkEgde<W> *_next;

        LinkEgde(const W &w) : _srcIndex(-1), _dstIndex(-1), _w(w), _next(nullptr) {}
    };

    template <class V, class W, bool Direction = false>
    class Graph
    {

        typedef LinkEgde<W> Edge;

    public:
        Graph(const V *vertexs, size_t n)
        {

            _vertexs.reserve(n);
            for (size_t i = 0; i < n; i++)
            {

                _vertexs.push_back(_vertexs[i]);
                _vIndexMap[_vertexs[i]] = i;
            }
            _linkTable.resize(n, nullptr);
        }
        size_t GetVertexIndex(const V &v)
        {

            auto ret = _vIndexMap.find(v);
            if (ret != _vIndexMap.end())
            {
                return ret->second;
            }
            else
            {
                throw invalid_argument("not exist vertex");
                return -1;
            }
        }

        void AddEdge(const V &src, const V &dst, const W &w)
        {

            size_t srcindex = GetVertexIndex(src);
            size_t dstindex = GetVertexIndex(dst);

            Edge *sd_edge = new Edge(w);
            sd_edge->_srcIndex = srcindex;
            sd_edge->_dstIndex = dstindex;
            sd_edge->_next = _linkTable[srcindex];
            _linkTable[srcindex] = sd_edge;

            //如果是无向图

            if (Direction == false)
            {

                Edge *ds_edge = new Edge(w);
                ds_edge->_srcIndex = dstindex;
                ds_edge->_dstIndex = srcindex;
                ds_edge->_next = _linkTable[dstindex];
                _linkTable[dstindex] = ds_edge;
            }
        }

          void BFS(const V & src){

            size_t srcindex=GetVertexIndex(src);
            vector<boo> visited;

            visited.resize(_vertexs.size(),false);
            queue<int> q;

            q.push(srcindex);
            visited[srcindex]=true;

            size_t d=1;
            size_t dSize=1;

            while(!q.empty()){
                printf("%s",src.c_str(),d);
                    while (d--)
            {
                size_t front=q.front();
                q.pop();
                for(size_t i=0;i<_vertexs.size();i++){

                    if(visited[i]!=true&&_matrix[front][i]!=MAX_W)

                    printf("[%d:%s]",i,_vertexs[i].c_str());
                    visited[i]=true;
                    q.push(i);
                }
            }
            cout<<endl;
        }

        
            

            
        }

    private:
        map<string, int> _vIndexMap;
        vector<V> _vertexs;        //顶点集合
        vector<Edge *> _linkTable; //边的集合
    };

    void TestGraph()
    {

        string a[] = {"zhangsan", "lisi", "wangwu", "zhaoliu"};
        Graph<string, int> g1(a, 4);
        g1.AddEdge("zhangsan", "lisi", 100);
        g1.AddEdge("zhangsan", "wangwu", 200);
        g1.AddEdge("wangwu", "zhaoliu", 30);
        g1.BFS("zhangsan");
    }


    

  

}

int main()
{

    LinkTable::TestGraph();

    system("pause");
    return 0;
}

1.2 图的深度优先遍历

void _DFS(int index, vector<bool>& visited)
{
 if(!visited[index])
 {
 cout<<_v[index]<<" ";
 visited[index] = true;
 LinkEdge* pCur = _linkEdges[index];
 while(pCur)
 {
 _DFS(pCur->_dst, visited);
 pCur = pCur->_pNext;
 }
 }
}
void DFS(const V& v)
{
 cout<<"DFS:";
 vector<bool> visited(_v.size(), false);
 _DFS(GetIndexOfV(v), visited);
 for(size_t index = 0; index < _v.size(); ++index)
 _DFS(index, visited);
 cout<<endl;
}
void TestGraphDBFS()
{
string a[] = { "张三", "李四", "王五", "赵六", "周七" };
Graph<string, int> g1(a, sizeof(a)/sizeof(string));
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.AddEdge("王五", "周七", 30);
g1.BFS("张三");
g1.DFS("张三");
}

4. 最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即： 从其中删去任何一条边，生成树

就不在连通；反之，在其中引入任何一条新边，都会形成一条回路 。

若连通图由 n 个顶点组成，则其生成树必含 n 个顶点和 n-1 条边。因此构造最小生成树的准则有三

条：

1. 只能使用图中的边来构造最小生成树

2. 只能使用恰好 n-1 条边来连接图中的 n 个顶点

3. 选用的 n-1 条边不能构成回路

构造最小生成树的方法： Kruskal 算法和 Prim 算法。这两个算法都采用了 逐步求解的贪心策略 。

贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是

整体最优的的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解

4.1 Kruskal算法

任给一个有n个顶点的连通网络N={V,E}，首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量，其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。如此重复，直到所有顶点在同一个连通分量上为止。核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。

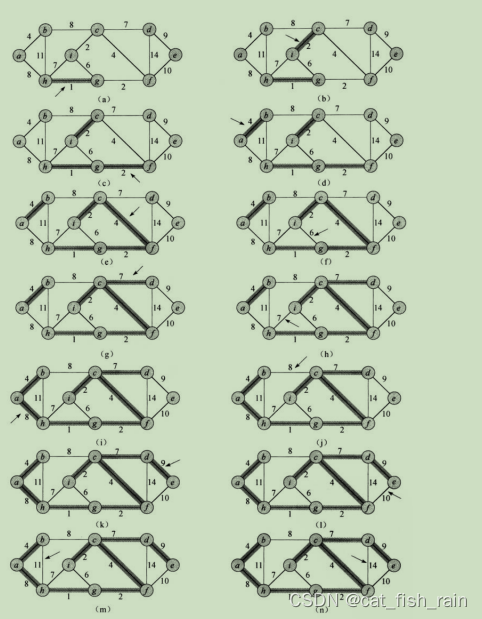
W Kruskal(Self& minTree)
{
     minTree._vertexs = _vertexs;
     minTree._vIndexMap = _vIndexMap;
     minTree._matrix.resize(_vertexs.size());
     for (auto& e : minTree._matrix)
 {
         e.resize(_vertexs.size(), MAX_W);
     }
     priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
     for (size_t i = 0; i < _matrix.size(); ++i)
     {
         for (size_t j = 0; j < _matrix[i].size(); ++j)
         {
             if (i < j && _matrix[i][j] != MAX_W)
             {
                 pq.push(Edge(i, j, _matrix[i][j]));
             }
         }
     }
     W total = W();
     // 贪心算法，从最小的边开始选
     size_t i = 1;
     UnionFindSet ufs(_vertexs.size());
     while (i < _vertexs.size() && !pq.empty())
     {
         Edge min = pq.top();
         pq.pop();
         // 边不在一个集合，说明不会构成环，则添加到最小生成树
         if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti))
         {
             //cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << 
":" << _matrix[min._srci][min._dsti] << endl;
             minTree._AddEdge(min._srci, min._dsti, min._w);
             total += min._w;
             ufs.Union(min._srci, min._dsti);
             ++i;
         }
     }
     if (i == _vertexs.size())
     {
         return total;
     }
     else
     {
         return W();
     }
}
void TestGraphMinTree()
{
     const char* str = "abcdefghi";
     Graph<char, int> g(str, strlen(str));
     g.AddEdge('a', 'b', 4);
     g.AddEdge('a', 'h', 8);
     //g.AddEdge('a', 'h', 9);
     g.AddEdge('b', 'c', 8);
     g.AddEdge('b', 'h', 11);
 g.AddEdge('c', 'i', 2);
     g.AddEdge('c', 'f', 4);
     g.AddEdge('c', 'd', 7);
     g.AddEdge('d', 'f', 14);
     g.AddEdge('d', 'e', 9);
     g.AddEdge('e', 'f', 10);
     g.AddEdge('f', 'g', 2);
     g.AddEdge('g', 'h', 1);
     g.AddEdge('g', 'i', 6);
     g.AddEdge('h', 'i', 7);
     Graph<char, int> kminTree;
     cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
     kminTree.Print();
     Graph<char, int> pminTree;
     cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
     pminTree.Print();
}

4.2 Prim算法

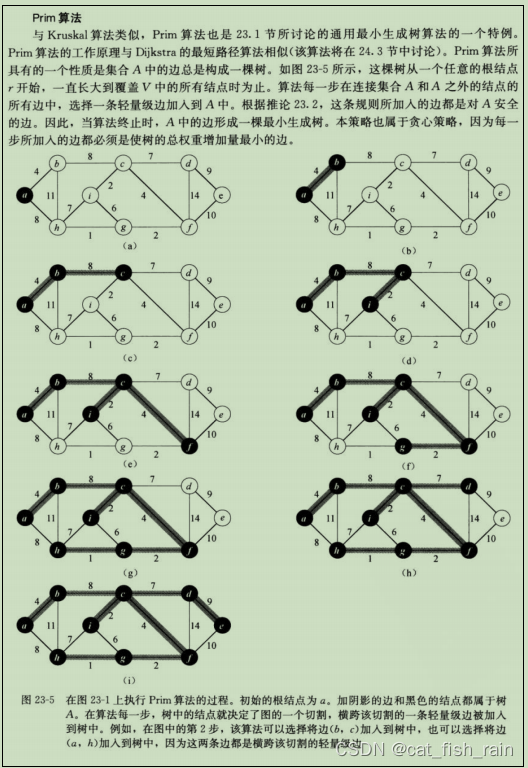
W Prim(Self& minTree, const V& src)
{
 minTree._vertexs = _vertexs;
 minTree._vIndexMap = _vIndexMap;
 minTree._matrix.resize(_vertexs.size());
 for (auto& e : minTree._matrix)
 {
 e.resize(_vertexs.size(), MAX_W);
 }
 size_t srci = GetVertexIndex(src);
set<size_t> inSet;
 inSet.insert(srci);
 priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
 for (size_t i = 0; i < _vertexs.size(); ++i)
 {
 if (_matrix[srci][i] != MAX_W)
 {
 pq.push(Edge(srci, i, _matrix[srci][i]));
 }
 }
 W total = W();
 while (inSet.size() < _vertexs.size() && !pq.empty())
 {
 Edge min = pq.top();
 pq.pop();
 // 防止环的问题
 if (inSet.find(min._srci) == inSet.end() ||
inSet.find(min._dsti) == inSet.end())
 {
 //cout << _vertexs[min._srci] << "-" << 
_vertexs[min._dsti] << ":" << _matrix[min._srci][min._dsti] << endl;
 minTree._AddEdge(min._srci, min._dsti, min._w);
 total += min._w;
 // 新入顶点的连接边进入队列
 for (size_t i = 0; i < _vertexs.size(); ++i)
 {
 if (_matrix[min._dsti][i] != MAX_W && inSet.find(i) 
== inSet.end())
 {
 pq.push(Edge(min._dsti, i, _matrix[min._dsti]
[i]));
 }
 }
 inSet.insert(min._dsti);
 }
 }
 if (inSet.size() == _vertexs.size())
 {
 return total;
 }
 else
 {
 return W();
 }
}
void TestGraphMinTree()
{
     const char* str = "abcdefghi";
     Graph<char, int> g(str, strlen(str));
     g.AddEdge('a', 'b', 4);
     g.AddEdge('a', 'h', 8);
//g.AddEdge('a', 'h', 9);
     g.AddEdge('b', 'c', 8);
     g.AddEdge('b', 'h', 11);
     g.AddEdge('c', 'i', 2);
     g.AddEdge('c', 'f', 4);
     g.AddEdge('c', 'd', 7);
     g.AddEdge('d', 'f', 14);
     g.AddEdge('d', 'e', 9);
     g.AddEdge('e', 'f', 10);
     g.AddEdge('f', 'g', 2);
     g.AddEdge('g', 'h', 1);
     g.AddEdge('g', 'i', 6);
     g.AddEdge('h', 'i', 7);
     Graph<char, int> kminTree;
     cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
     kminTree.Print();
     Graph<char, int> pminTree;
     cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
     pminTree.Print();
}

5. 最短路径

最短路径问题：从在带权有向图 G 中的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。

5.1单源最短路径--Dijkstra算法

单源最短路径问题：给定一个图 G = ( V ， E ) G=(V ， E)G=(V ， E) ，求源结点 s ∈ V s ∈ Vs ∈ V 到图

中每个结点 v ∈ V v ∈ Vv ∈ V 的最短路径。 Dijkstra 算法就适用于解决带权重的有向图上的单源最短

路径问题， 同时算法要求图中所有边的权重非负 。一般在求解最短路径的时候都是已知一个起点

和一个终点，所以使用 Dijkstra 算法求解过后也就得到了所需起点到终点的最短路径。

针对一个带权有向图 G ，将所有结点分为两组 S 和 Q ， S 是已经确定最短路径的结点集合，在初始时

为空（初始时就可以将源节点 s 放入，毕竟源节点到自己的代价是 0 ）， Q 为其余未确定最短路径

的结点集合， 每次从 Q 中找出一个起点到该结点代价最小的结点 u ，将 u 从 Q 中移出，并放入 S

中，对 u 的每一个相邻结点 v 进行松弛操作 。松弛即对每一个相邻结点 v ，判断源节点 s 到结点 u

的代价与 u 到 v 的代价之和是否比原来 s 到 v 的代价更小，若代价比原来小则要将 s 到 v 的代价更新

为 s 到 u 与 u 到 v 的代价之和，否则维持原样。如此一直循环直至集合 Q 为空，即所有节点都已经

查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法循环后其代价仍为初始设定

的值，不发生变化。 Dijkstra 算法每次都是选择 V-S 中最小的路径节点来进行更新，并加入 S 中，所

以该算法使用的是贪心策略。

Dijkstra 算法存在的问题是不支持图中带负权路径，如果带有负权路径，则可能会找不到一些路

径的最短路径。

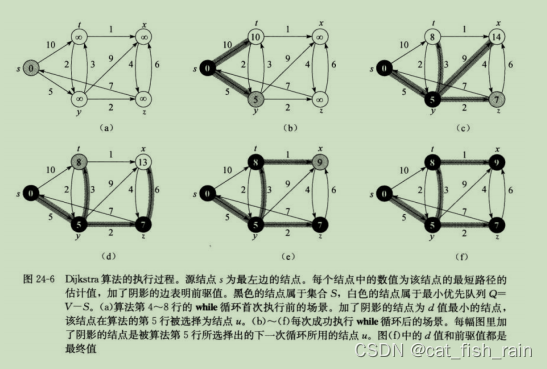
void Dijkstra(const V& src, vector<W>& dist, vector<int>& parentPath)
{
size_t N = _vertexs.size();
size_t srci = GetVertexIndex(src);
// vector<W> dist,记录srci-其他顶点最短路径权值数组
dist.resize(N, MAX_W);
// vector<int> parentPath 记录srci-其他顶点最短路径父顶点数组
parentPath.resize(N, -1);
// 标记是否找到最短路径的顶点集合S
vector<bool> S;
S.resize(N, false);
// srci的权值给一个最小值，方便贪心第一次找到这个节点
dist[srci] = W(); 
// N个顶点更新N次
for (size_t i = 0; i < N; ++i)
 {
     // 贪心算法：srci到不在S中路径最短的那个顶点u
     W min = MAX_W;
     size_t u = srci;
     for (size_t j = 0; j < N; ++j)
     {
         if (S[j] == false && dist[j] < min)
         {
             min = dist[j];
             u = j;
         }
     }
     S[u] = true;
     // 松弛算法：更新一遍u连接的所有边，看是否能更新出更短连接路径
     for (size_t k = 0; k < N; ++k)
     {
// 如果srci->u + u->k 比 srci->k更短 则进行更新
         if (S[k] == false && _matrix[u][k] != MAX_W
             && dist[u] + _matrix[u][k] < dist[k])
         {
             dist[k] = dist[u] + _matrix[u][k];
             parentPath[k] = u;
         }
     }
 }
}
// 打印最短路径的逻辑算法
void PrinrtShotPath(const V& src, const vector<W>& dist, const vector<int>&
parentPath)
{
 size_t N = _vertexs.size();
 size_t srci = GetVertexIndex(src);
 for (size_t i = 0; i < N; ++i)
 {
 if (i == srci)
 continue;
 
 vector<int> path;
 int parenti = i;
 while (parenti != srci)
 {
 path.push_back(parenti);
 parenti = parentPath[parenti];
 }
 path.push_back(srci);
 reverse(path.begin(), path.end());
 for (auto pos : path)
 {
 cout << _vertexs[pos] << "->";
 }
 cout << dist[i] << endl;
 }
}
void TestGraphDijkstra()
{
const char* str = "syztx";
Graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('s', 't', 10);
g.AddEdge('s', 'y', 5);
g.AddEdge('y', 't', 3);
g.AddEdge('y', 'x', 9);
g.AddEdge('y', 'z', 2);
g.AddEdge('z', 's', 7);
g.AddEdge('z', 'x', 6);
g.AddEdge('t', 'y', 2);
g.AddEdge('t', 'x', 1);
g.AddEdge('x', 'z', 4);
vector<int> dist;
vector<int> parentPath;
g.Dijkstra('s', dist, parentPath);
g.PrinrtShotPath('s', dist, parentPath);
// 图中带有负权路径时，贪心策略则失效了。
// 测试结果可以看到s->t->y之间的最短路径没更新出来
/*const char* str = "sytx";
 Graph<char, int, INT_MAX, true> g(str, strlen(str));
 g.AddEdge('s', 't', 10);
 g.AddEdge('s', 'y', 5);
 g.AddEdge('t', 'y', -7);
 g.AddEdge('y', 'x', 3);
 vector<int> dist;
 vector<int> parentPath;
 g.Dijkstra('s', dist, parentPath);
 g.PrinrtShotPath('s', dist, parentPath);*/
}

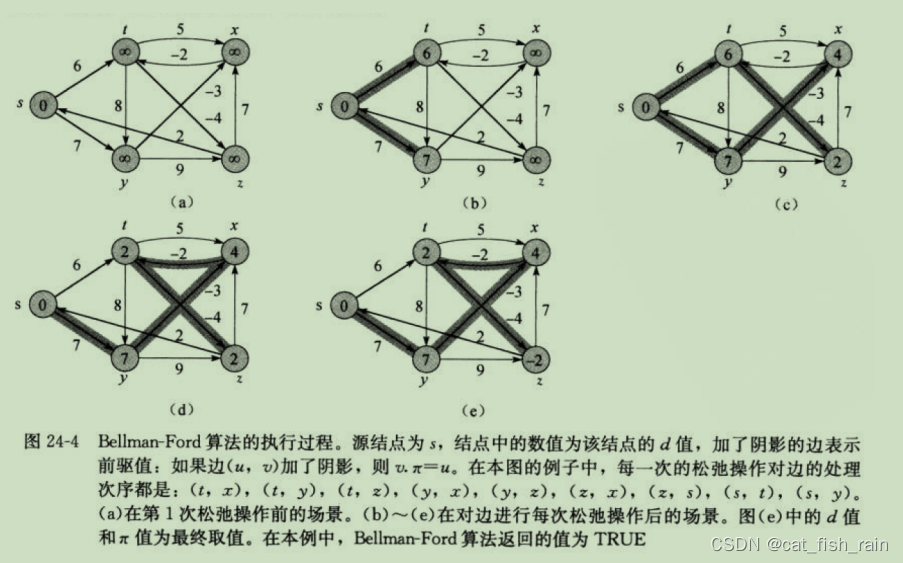
5.2 单源最短路径--Bellman-Ford算法

Dijkstra 算法只能用来解决正权图的单源最短路径问题，但有些题目会出现负权图。这时这个算法

就不能帮助我们解决问题了，而 bellman—ford 算法可以解决负权图的单源最短路径问题 。它的

优点是可以解决有负权边的单源最短路径问题，而且可以用来判断是否有负权回路。它也有明显

的缺点，它的时间复杂度 O(N*E) (N 是点数， E 是边数 ) 普遍是要高于 Dijkstra 算法 O(N²) 的。像这里

如果我们使用邻接矩阵实现，那么遍历所有边的数量的时间复杂度就是 O(N^3) ，这里也可以看出

来 Bellman-Ford 就是一种暴力求解更新。

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& parentPath)
{
 size_t N = _vertexs.size();
 size_t srci = GetVertexIndex(src);
 // vector<W> dist,记录srci-其他顶点最短路径权值数组
 dist.resize(N, MAX_W);
// vector<int> parentPath 记录srci-其他顶点最短路径父顶点数组
 parentPath.resize(N, -1);
 // 先更新srci->srci为最小值
 dist[srci] = W();
 for (size_t k = 0; k < N - 1; ++k)
 {
 bool exchange = false;
 for (size_t i = 0; i < N; ++i)
 {
 for (size_t j = 0; j < N; ++j)
 {
 // srci->i + i->j < srci->j 则更新路径及权值
 if (_matrix[i][j] != MAX_W
 && dist[i] + _matrix[i][j] < dist[j])
 {
 dist[j] = dist[i] + _matrix[i][j];
 parentPath[j] = i;
 exchange = true;
 }
 }
 }
 if (exchange == false)
 break;
 }
 for (size_t i = 0; i < N; ++i)
 {
 for (size_t j = 0; j < N; ++j)
 {
 // 检查有没有负权回路
 if (_matrix[i][j] != MAX_W
 && dist[i] + _matrix[i][j] < dist[j])
 {
 return false;
 }
 }
 }
 return true;
}
void TestGraphBellmanFord()
{
 const char* str = "syztx";
 Graph<char, int, INT_MAX, true> g(str, strlen(str));
 g.AddEdge('s', 't', 6);
 g.AddEdge('s', 'y', 7);
 g.AddEdge('y', 'z', 9);
 g.AddEdge('y', 'x', -3);
 g.AddEdge('z', 's', 2);
 g.AddEdge('z', 'x', 7);
 g.AddEdge('t', 'x', 5);
 g.AddEdge('t', 'y', 8);
 g.AddEdge('t', 'z', -4);
g.AddEdge('x', 't', -2);
 vector<int> dist;
 vector<int> parentPath;
 if (g.BellmanFord('s', dist, parentPath))
 {
 g.PrinrtShotPath('s', dist, parentPath);
 }
 else
 {
 cout << "存在负权回路" << endl;
 }
 // 微调图结构，带有负权回路的测试
 //const char* str = "syztx";
 //Graph<char, int, INT_MAX, true> g(str, strlen(str));
 //g.AddEdge('s', 't', 6);
 //g.AddEdge('s', 'y', 7);
 //g.AddEdge('y', 'x', -3);
 //g.AddEdge('y', 'z', 9);
 //g.AddEdge('y', 'x', -3);
 //g.AddEdge('y', 's', 1); // 新增
 //g.AddEdge('z', 's', 2);
 //g.AddEdge('z', 'x', 7);
 //g.AddEdge('t', 'x', 5);
 //g.AddEdge('t', 'y', -8); // 更改
 //g.AddEdge('t', 'z', -4);
 //g.AddEdge('x', 't', -2);
 //vector<int> dist;
 //vector<int> parentPath;
 //if (g.BellmanFord('s', dist, parentPath))
 //{
 // g.PrinrtShotPath('s', dist, parentPath);
 //}
 //else
 //{
 // cout << "存在负权回路" << endl;
 //}
}

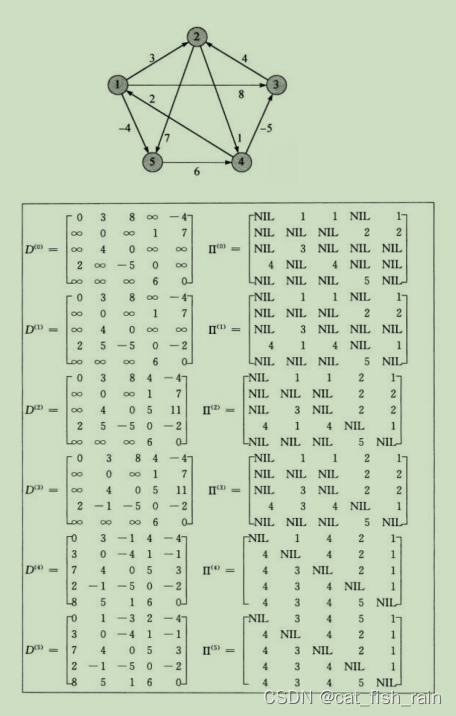
5.3 多源最短路径--Floyd-Warshall算法

Floyd-Warshall 算法是解决任意两点间的最短路径的一种算法。Floyd算法考虑的是一条最短路径的中间节点，即简单路径 p={v1,v2,…,vn} 上除 v1 和 vn 的任意节点。

设 k 是 p 的一个中间节点，那么从 i 到 j 的最短路径 p 就被分成 i 到 k 和 k 到 j 的两段最短路径 p1 ， p2 。 p1

是从 i 到 k 且中间节点属于 {1 ， 2 ， … ， k-1} 取得的一条最短路径。 p2 是从 k 到 j 且中间节点属于 {1 ，

2 ， … ， k-1} 取得的一条最短路径。

即 Floyd 算法本质是三维动态规划， D[i][j][k] 表示从点 i 到点 j 只经过 0 到 k 个点最短路径，然后建立

起转移方程，然后通过空间优化，优化掉最后一维度，变成一个最短路径的迭代算法，最后即得

到所以点的最短路。

void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>&
vvParentPath)
{
 size_t N = _vertexs.size();
 vvDist.resize(N);
 vvParentPath.resize(N);
// 初始化权值和路径矩阵
 for (size_t i = 0; i < N; ++i)
 {
 vvDist[i].resize(N, MAX_W);
 vvParentPath[i].resize(N, -1);
 }
 // 将直接相连的路径初始化
 for (size_t i = 0; i < N; ++i)
 {
 for (size_t j = 0; j < N; ++j)
 {
 if (_matrix[i][j] != MAX_W)
 { 
 vvDist[i][j] = _matrix[i][j];
 vvParentPath[i][j] = i;
 }
 else
 {
 vvParentPath[i][j] = -1;
 }
 if (i == j)
 {
 vvDist[i][j] = 0;
 vvParentPath[i][j] = -1;
 }
 }
 }
 // 依次用顶点k作为中转点更新最短路径
 for (size_t k = 0; k < N; ++k)
 {
 for (size_t i = 0; i < N; ++i)
 {
 for (size_t j = 0; j < N; ++j)
 {
 // i->k + k->j 比 i->j前面更新的距离更短，则更新
 if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
 && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
 {
 vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
 vvParentPath[i][j] = vvParentPath[k][j];
 }
 }
 }
 // 打印权值和路径矩阵观察数据
 //for (size_t i = 0; i < N; ++i)
 //{
 // for (size_t j = 0; j < N; ++j)
 // {
 // if (vvDist[i][j] == MAX_W)
 // {
 // //cout << "*" << " ";
 // printf("%3c", '*');
 // }
 // else
// {
 // //cout << vvDist[i][j] << " ";
 // printf("%3d", vvDist[i][j]);
 // }
 // }
 // cout << endl;
 //}
 //cout << endl;
 //for (size_t i = 0; i < N; ++i)
 //{
 // for (size_t j = 0; j < N; ++j)
 // {
 // //cout << vvParentPath[i][j] << " ";
 // printf("%3d", vvParentPath[i][j]);
 // }
 // cout << endl;
 //}
 //cout << "=================================" << endl;
 }
}
void TestFloydWarShall()
{
 const char* str = "12345";
 Graph<char, int, INT_MAX, true> g(str, strlen(str));
 g.AddEdge('1', '2', 3);
 g.AddEdge('1', '3', 8);
 g.AddEdge('1', '5', -4);
 g.AddEdge('2', '4', 1);
 g.AddEdge('2', '5', 7);
 g.AddEdge('3', '2', 4);
 g.AddEdge('4', '1', 2);
 g.AddEdge('4', '3', -5);
 g.AddEdge('5', '4', 6);
 vector<vector<int>> vvDist;
 vector<vector<int>> vvParentPath;
 g.FloydWarShall(vvDist, vvParentPath);
 // 打印任意两点之间的最短路径
 for (size_t i = 0; i < strlen(str); ++i)
 {
 g.PrinrtShotPath(str[i], vvDist[i], vvParentPath[i]);
 cout << endl;
 }
}