“ 本篇文章对金鹰优化算法进行改进，首先通过引入混沌映射机制，对其群体进行初始化，增加金鹰个体的多样性；然后在金鹰个体的位置更新公式上引入改进的莱维飞行机制，提高搜索精度，帮助金鹰个体跳出局部最优。”

可以选择1-10不同的映射，1-10分别为，tent、Logistic、Cubic、chebyshev、Piecewise、sinusoidal、Sine,ICMIC, Circle,Bernoulli。选择不同的数字可以随意切换。

先上结果图，在CEC2005函数上进行测试，种群个体设置为50个，循环次数为1000次。

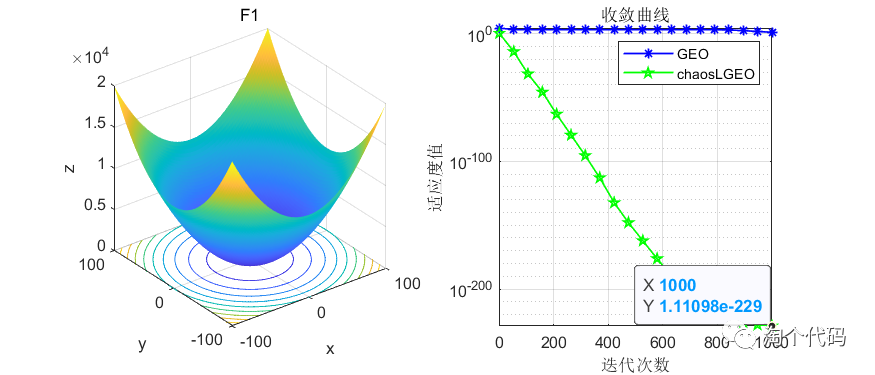
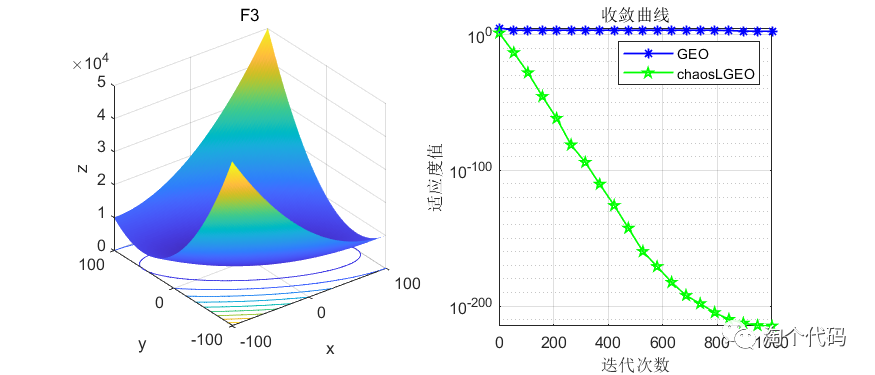
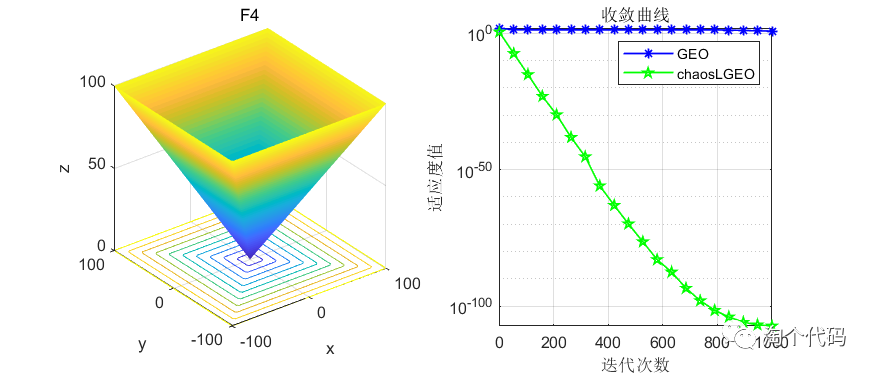
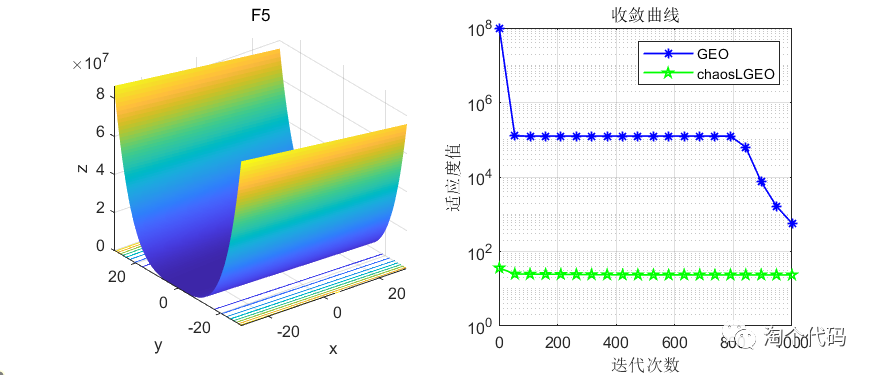
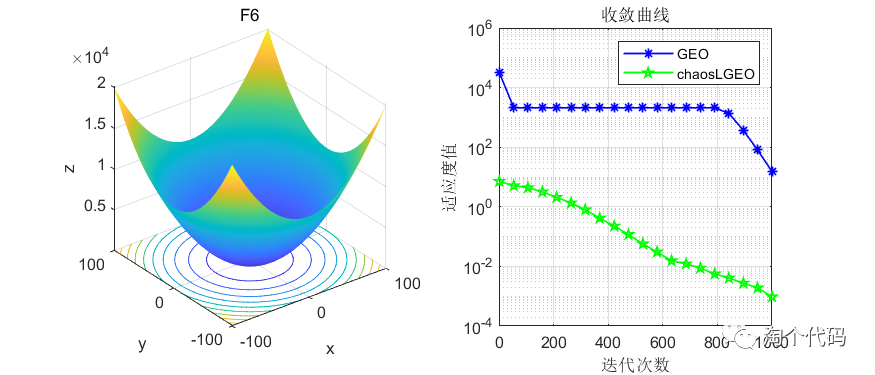
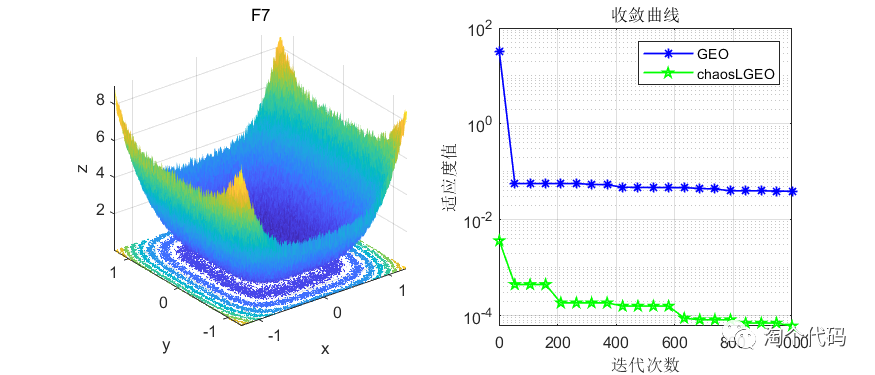
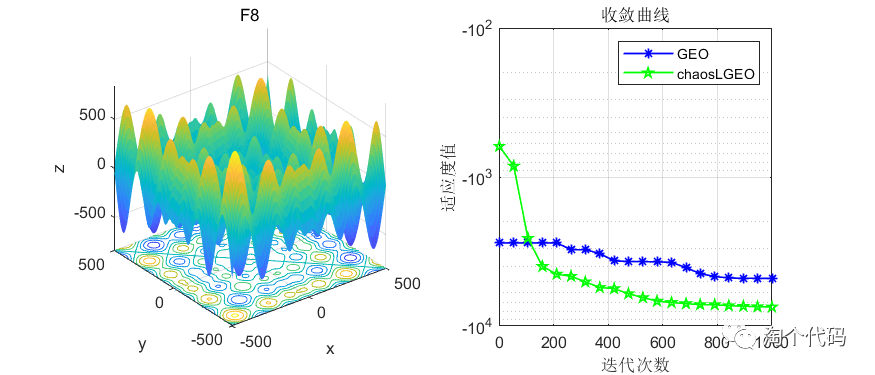
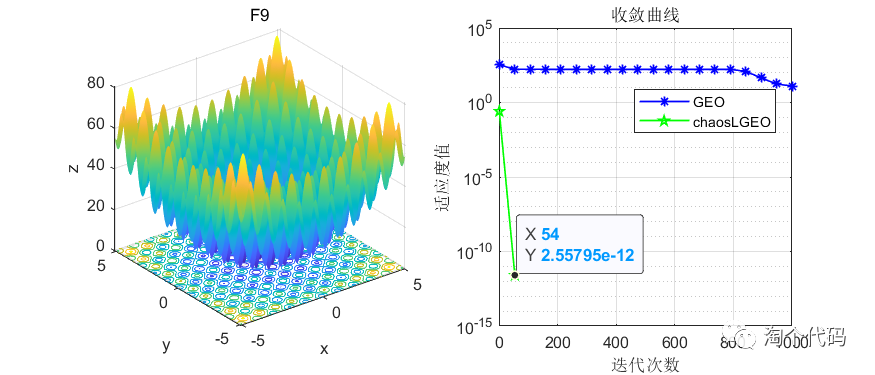
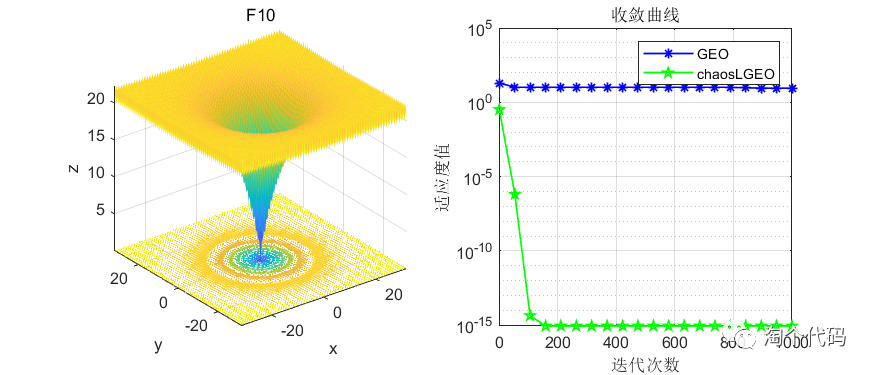
这里截选了前10个函数进行展示，可以看到改进前后在收敛速度和寻优精度上都有了很大的改进。

接下来讲一下改进的原理。

1. 混沌映射

   依旧是采用之前文章提到的10种混沌映射，可以自由切换映射方法，本文选取的映射方法是Logistic映射，大家也可以自行更改。没看过之前文章的小伙伴可以看一下。(1条消息) 10种混沌映射优化灰狼算法，可一键切换，可用于优化所有群智能算法，以灰狼算法为例进行介绍..._今天吃饺子的博客-CSDN博客

2. 改进的莱维飞行机制

    本文莱维飞行的添加并非如其他文章那样，直接在粒子更新的时候加上莱维系数，而是稍作改进，这样的效果也确实比直接加莱维系数要好。原理公式如下：

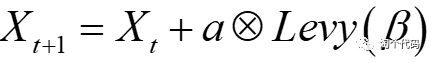
其中 , α是步长缩放因子，Levy(β)是萊维随机路径。

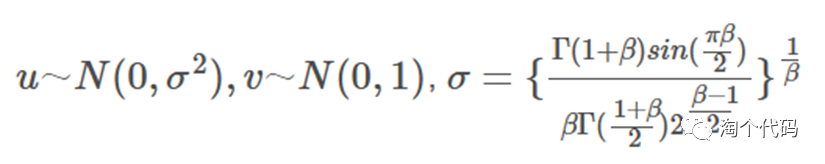
改进的原理如下：

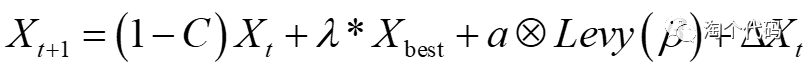
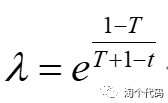
这么做的目的是将金鹰算法与莱维飞行进行优势互补，可以动态的调整每次寻优的比例系数。

代码如下：

%%
clear
clc
close all
%% Inputs 
number='F10'; %选定优化函数，自行替换:F1~F23
% [lb,ub,D,y]：下界、上界、维度、目标函数表达式
[lb,ub,nvars,fun]=CEC2005(number);  
% FunctionNumber =6; % 1-23
options.PopulationSize = 50;
options.MaxIterations  = 1000;
%% Run Multi-Objective Golden Eagle Optimizer 


options.AttackPropensity = [0.5 ,   2];
options.CruisePropensity = [0.1   , 0.5];
numm = 2; % 混沌映射：1-10分别为，tent、Logistic、Cubic、chebyshev、Piecewise、sinusoidal、Sine,ICMIC, Circle,Bernoulli
[chaosLx,chaosLfval,chaosLConvergenceCurve] = chaosLGEO (numm,fun,nvars,lb,ub, options); %调用改进的GEO算法
[x,fval,ConvergenceCurve] = GEO (fun,nvars,lb,ub, options);  %调用GEO


%% Figure
maxcycle = options.MaxIterations;
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(number)
title(number)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=20;
k=round(linspace(1,options.MaxIterations,CNT)); %随机选50个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:options.MaxIterations;
semilogy(iter(k),ConvergenceCurve(k),'b-*','linewidth',1);
hold on
semilogy(iter(k),chaosLConvergenceCurve(k),'g-p','linewidth',1);
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('GEO','chaosLGEO')
set (gcf,'position', [200,300,700,300])

注意看第16行变量numm，可以选择1-10不同的映射，1-10分别为，tent、Logistic、Cubic、chebyshev、Piecewise、sinusoidal、Sine,ICMIC, Circle,Bernoulli。选择不同的数字可以随意切换。

获取完整代码方式，下方卡片回复关键词：LGEO